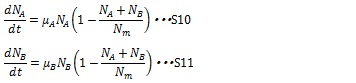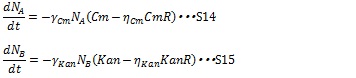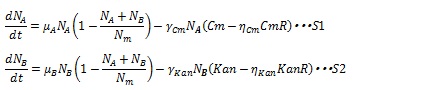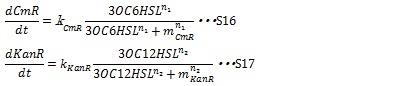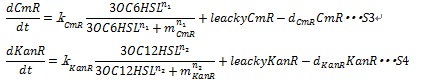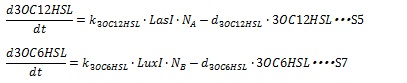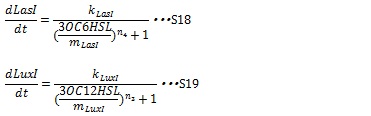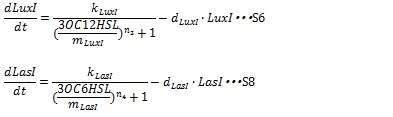Team:Tokyo Tech/Project/Artificial Cooperation System/modeling
From 2010.igem.org
(→Abstract) |
|||
| Line 11: | Line 11: | ||
==Mathematical modeling== | ==Mathematical modeling== | ||
| - | =Abstract= | + | =Mathematical modeling= |
| + | ==Abstract== | ||
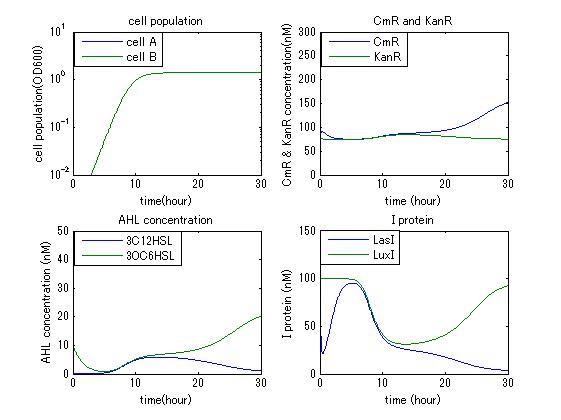
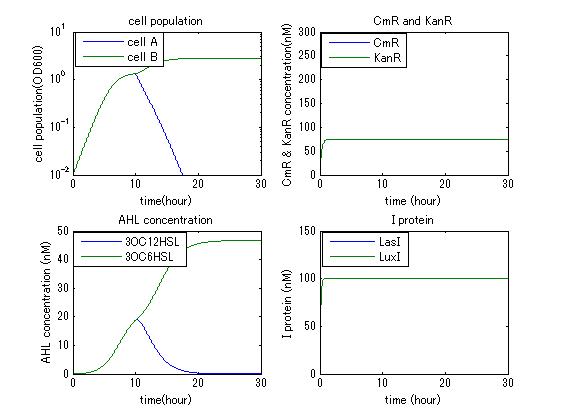
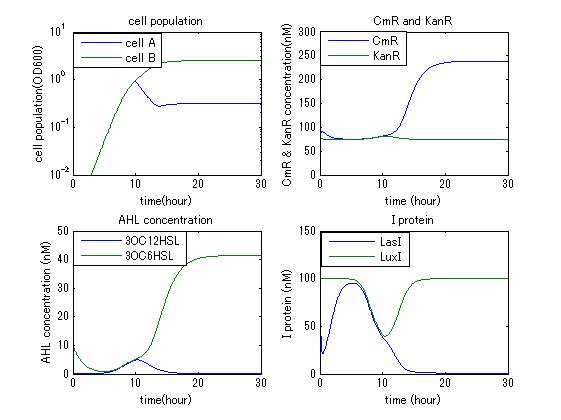
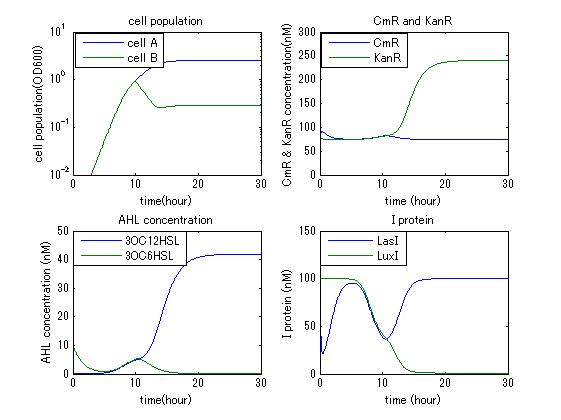
| + | In order to confirm that this system is feasible, we simulated this system and confirmed that this system can work. The following figures 〇〇 show the simulation result. Fig 〇 is the simulation result in the absence of antibiotic. Fig〇is the simulation result when cell A and cell B don’t have the Artificial Cooperation System. Fig 〇 is the simulation result in the case of addition of chloramphenicol. Fig 〇is the simulation result in the case of addition of kanamycin. Both results show that decreased AHL of dying cell activates the production of helper’s I protein and AHL, in consequence, resistance gene of dying cell is activated and dying cell is helped. From this simulation we confirmed that our Artificial Cooperation System is feasible system. | ||
| - | = | + | [[IMAGE: tokyotech_no_anti_sim_result.jpg|250px|left|thumb|Fig]] |
| - | In order to | + | [[IMAGE: tokyotech_no_system_sim_result.jpg|250px|left|thumb|Fig]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[IMAGE: tokyotech_cm_sim_result.jpg|250px|left|thumb|Fig]] | ||
| + | [[IMAGE: tokyotech_kan_sim_result.jpg|250px|left|thumb|Fig]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Model development== | ||
| + | In order to confirm the feasibility of Artificial Cooperation System, a mathematical model with ordinary differential equations (ODEs) is used to simulate the system. The state variables and parameters are described in detail in Table1. | ||
[[IMAGE:Tokyotech_S1-S8.jpg|400px]] | [[IMAGE:Tokyotech_S1-S8.jpg|400px]] | ||
| Line 78: | Line 123: | ||
d<sub>LuxI</sub>and d<sub>LasI</sub> are constant coefficient. | d<sub>LuxI</sub>and d<sub>LasI</sub> are constant coefficient. | ||
| + | |||
| + | |||
| + | ==Simulation result== | ||
Revision as of 09:01, 27 October 2010
Contents |
Mathematical modeling
Mathematical modeling
Abstract
In order to confirm that this system is feasible, we simulated this system and confirmed that this system can work. The following figures 〇〇 show the simulation result. Fig 〇 is the simulation result in the absence of antibiotic. Fig〇is the simulation result when cell A and cell B don’t have the Artificial Cooperation System. Fig 〇 is the simulation result in the case of addition of chloramphenicol. Fig 〇is the simulation result in the case of addition of kanamycin. Both results show that decreased AHL of dying cell activates the production of helper’s I protein and AHL, in consequence, resistance gene of dying cell is activated and dying cell is helped. From this simulation we confirmed that our Artificial Cooperation System is feasible system.
Model development
In order to confirm the feasibility of Artificial Cooperation System, a mathematical model with ordinary differential equations (ODEs) is used to simulate the system. The state variables and parameters are described in detail in Table1.
The major kinetic events in the Artificial Cooperation System that determine the behavior are: cell population growth; resistance gene expression under the control of quorum sensing activation promoters; AHLs synthesis and degradation; I protein synthesis under the control of quorum sensing repressive promoters. The interaction of 8 variables decides the performance of our Artificial Cooperation System. Following sentences describe how dynamic equations are developed.
I, Cell Population Growth
The growth state of individual cell without effect of antibiotics can be described by logistic growth law(S9). N in the equation S9 represents the cell population and Nm represents the maximum allowed number of cells due to nutrient limitation, μ is a constant coefficient.
The growth rate is proportional to cell population and inhibited by themselves due to nutrient limitation. The growth of mixed two types of cell can be described as equation S10 and S11. The growth rate of any kind of cell is proportional to its population but inhibited by total population of two types of cell (1-(NA+ NB)/ Nm)
The inhibition of antibiotics is represented by equation S12 and S13, where Cm and Kan represent chloramphenicol and kanamycin concentration respectively. And the γ is the rate constant. Antibiotics concentration and the number of cell contribute the decreasing rate.
The expression of antibiotics resistance gene can release the antibiotic inhibition to some extent according to the synthesized enzyme concentration. So S12 and S13 are replaced by equation S14 and S15, in which CmR and KanR are the expression level of antibiotics genes and η is constant for specific gene.
But, if (Cm-ηCmCmR) or (Kan-ηKanKanR) is negative, these terms are set to zero during simulation. Therefore, the dynamics of cell population are listed as equation S1 and S2.
II, Resistance gene expression under the control of AHLs In our system, the expression level of resistance gene is controlled by a complicated process which includes the combination of AHL to R protein, initialization of transcription and translation. R proteins, LuxR and LasR, are expressed constitutively and the concentration is supposed to be constant. Thus the expression of resistance genes could be generated by Hill function (equation S16 and S17) according to the concentration of AHLs.
Together with leakyCmR and leakyKanR that represent the leaky expression of the resistance genes and the degradation of resistance genes products, equation S3 and S4 are employed to simulate the expression of resistance genes.
Here, kCmR and kKanR are the max expression rate of the promoters. n1 and n2 are Hill coefficient. mCm and mKanR represent the AHL concentration producing half level of resistance gene products.
III, AHL synthesis and degradation AHL is synthesized by I protein and we assume that the concentration of substrates of AHL are constant, so the AHL synthetic rate is assumed to be proportional to the cognate I protein. And AHL synthetic rate is dependent on cell population, so synthetic rate is proportional to cell population. And the degradation rate of AHL is assumed to decay with first-order kinetic. Therefore, the dynamic equation of AHLs concentration are listed in equation S5 and S7.
k3OC6HSL, k3OC12HSL, d3OC6HSL and d3OC12HSL are constant coefficients.
IV, I protein production under the control of AHL dependent promoter The expression of I proteins can be generated by Hill function according to the concentration of AHL like the expression of resistance gene. Though the resistance genes are activated by AHLs, the production of I proteins is repressed by AHLs. So, we employ the following Hill function (equation S18 and S19)
kLuxI and kLasI represent maximum production rate of LuxI and LasI. So when the concentration of AHL is 0nM, the I protein production rate is k. n3 and n4 are Hill coefficients. mLuxI and mLasIrepresent the AHL concentration producing half level of I proteins. Therefore dynamics equations of I proteins production are listed in equation S6 and S8.
dLuxIand dLasI are constant coefficient.
Simulation result
 "
"