Team:Imperial College London/Modelling/Signalling/Results and Conclusion

From 2010.igem.org

Modelling	Overview \| Detection Model \| Signaling Model \| Fast Response Model \| Interactions
A major part of the project consisted of modelling each module. This enabled us to decide which ideas we should implement. Look at the Fast Response page for a great example of how modelling has made a major impact on our design!

Objectives | Description | Results | Constants | MATLAB Code

Results and Conclusion

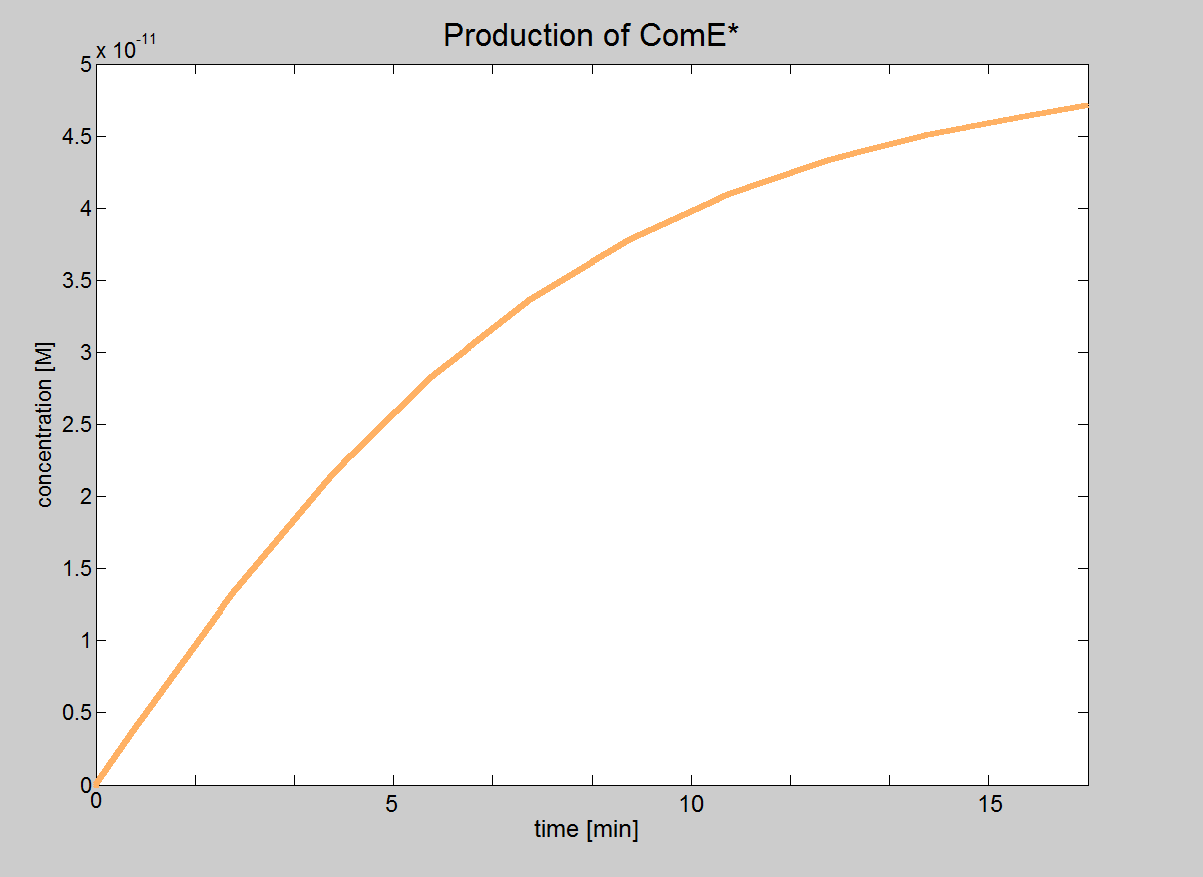
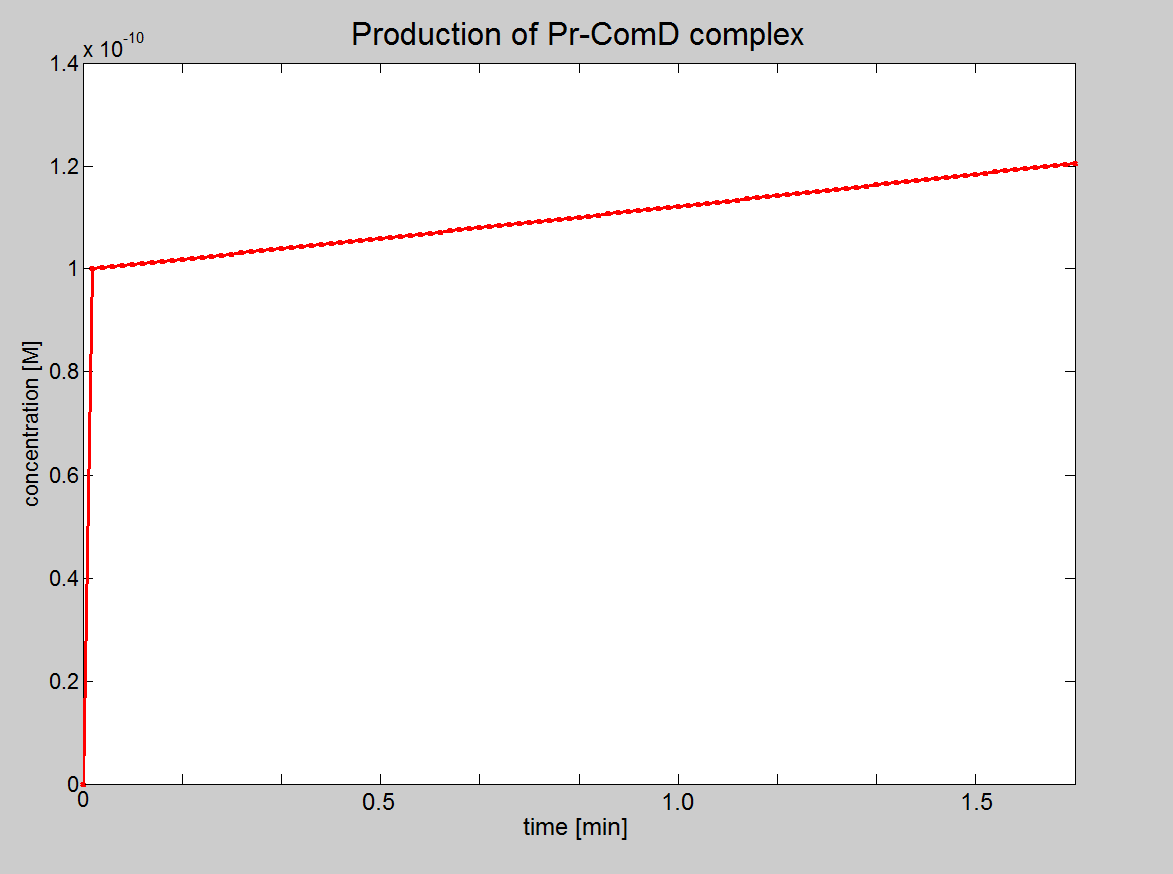
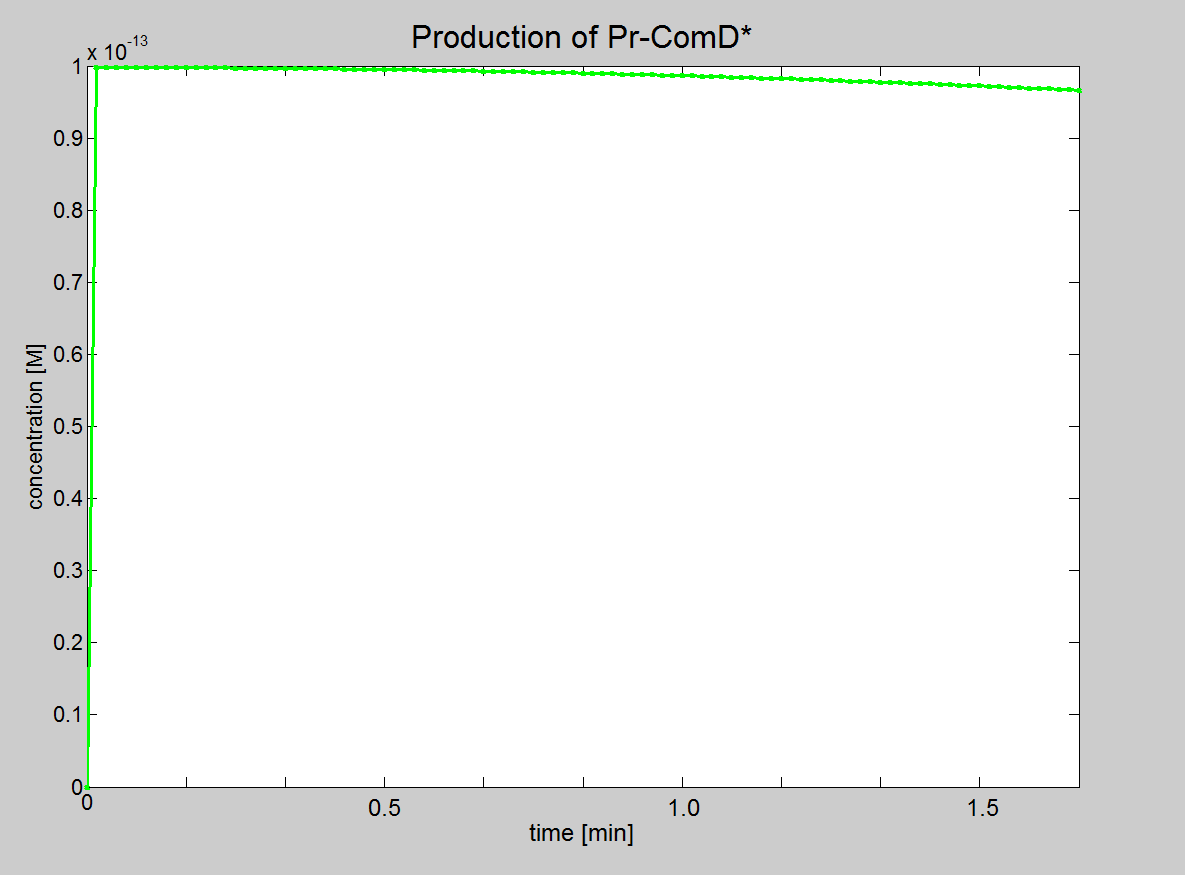
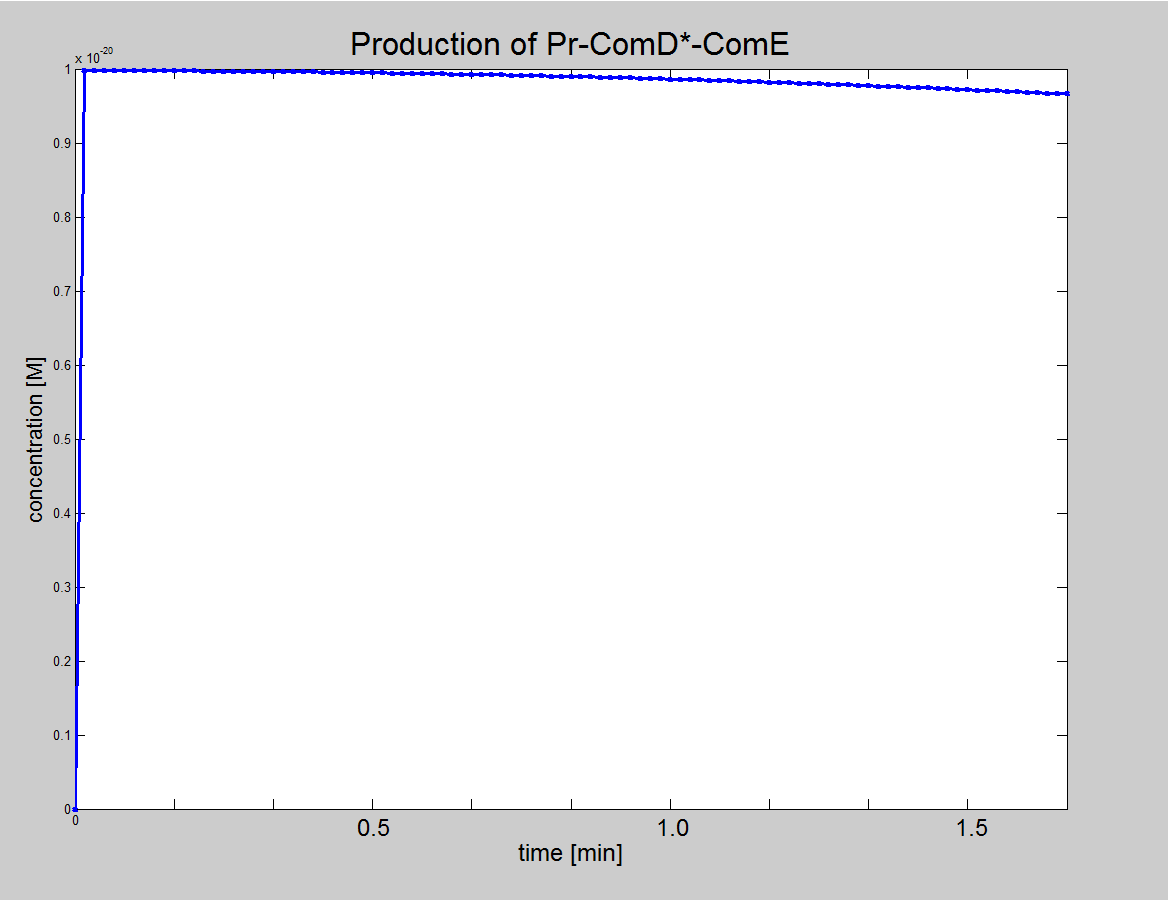
Using this model, we can show that the phosphorylated, ComE*, is proportional to both initial concentration of AIP and ComD.

If the initial concentration of AIP or ComD is zero, there is no formation of ComE*. We are assuming an initial concentration of Phosphate and ComE of 100nM. If we change either [AIP]₀ or [ComE]₀, then the final concentration of ComE* will always tend towards 5×10^-11M. [ComE*]_final will always tend towards this value, unless the initial concentrations of Phosphate and ComE are changed. However, if we increase both [AIP]₀ and [ComE]₀ at the same time, then [ComE*]_final will be reached much faster (i.e. slope increases).

Equation: AIP-ComD*-ComE ↔ AIP-ComD + ComE*

Graph showing how [ComE*]_final eventually reaches the value 5×10^-11M.

1. Graph showing the production of Pr-ComD complex. (Equation 1: AIP + ComD ↔ AIP-ComD).

2. Graph showing the production of phosphorylated Pr-ComD* complex. (Equation 2: AIP-ComD + Phosphate ↔ AIP-ComD*).

3. Graph showing the production of Pr-ComD*-ComE complex. (Equation 3: AIP-ComD* + ComE ↔ AIP-ComD*-ComE.

Notice the steep increase of concentration for each of the graphs, which could be due to high k_1,2,3 values.

Click here for the constants of this model...