Team:Imperial College London/Modelling/Protein Display/Detailed Description

From 2010.igem.org

(Difference between revisions)

Revision as of 17:02, 26 October 2010

Department of Bioengineering

Division of Molecular Biosciences

Modelling	Overview \| Detection Model \| Signaling Model \| Fast Response Model \| Interactions
A major part of the project consisted of modelling each module. This enabled us to decide which ideas we should implement. Look at the Fast Response page for a great example of how modelling has made a major impact on our design!

Objectives | Description | Results | Constants | MATLAB Code

Detailed Description

This model consists of 5 parts that had to be developed:

Identification of all active and relevant elements of the isolated part of the system.
Identification of interactions between the identified elements.
Identification of threshold concentration of auto inducing peptide (AIP) needed for activation of the receptor.
Determining the volume of cell wall.
Defining a control volume around the bacterial cell (after cleavage, the surface protein will float around in the extracellular environment).
Determining the importance of localised concentrations in a Control Volume.
Determining the surface protein production to estimate the maximum abundance on the bacterial surface.

1. Elements of the system

The surface protein consists of a cell wall binding domain, linker, AIP (Auto Inducing Peptide). It is expressed by constitutive gene expression. It was assumed that the bacteria would be fully grown before carrying out the detection so the cell wall would be covered with as many surface proteins as the cell can maintain.
Schistosoma elastase (enzyme released by the parasite) cleaves the AIP from the cell wall binding domain at the linker site. In the laboratory we used TEV protease as we could not get hold of Schistosoma elastase, so the model was adjusted appropriately (TEV enzyme kinetic parameters were used).
The ComD receptor is activated by a sufficiently high AIP concentration. Once activated, ComD signals into the cell to activate the colour response.

2. Interactions between elements

Apart from the proteins being expressed from genes, there was only one more chemical reaction identified in this part of the system. This is the cleavage of proteins, which is an enzymatic reaction:

Substrate (S) = Protein
Enzyme (E) = TEV (Protease)
Product (P) = Peptide

This enzymatic reaction can be rewritten as ordinary differential equations (ODEs), which is of similar form as the 1-step amplification model. However, most of the constants and initial concentrations are different.

This model is quite peculiar as we realised that its behaviour is not only dependent on time, but space as well. Namely, the cleavage reaction happens on the cell wall of bacteria. However, AIP that has already been cleaved is allowed to diffuse in any direction. Since we were not sure how to model this scenario, we decided to determine the importance of localised concentrations in a Control Volume.

3. Threshold concentration of AIP

The optimal peptide concentration required to activate ComD is 10 ng/ml [1]. This is the threshold value for ComD activation. However, the minimum concentration of peptide to give a detectable activation is 0.5ng/ml.
The threshold for the minimal activation of the receptor is c_th=4.4658×10^-9 mol/L. Click on the button below to uncover the calculations.

Converting 10 ng/ml to 4.4658×10^-9 mol/L

The mass of a peptide is 2.24kDa = 3.7184×10^-21g.
The number of molecules in one ml is 10ng/3.7184×10^-21g = 2.6893×10¹². In a litre, the number of molecules is 2.6893×10¹⁵molecules/L.
Dividing this value by Avogadro's constant gives the threshold concentration of c_th=4.4658×10^-9 mol/L.
The threshold for minimal activation of receptor is 2.2329×10^-10 mol/L.

4. Cell Wall Volume

The volume of the cell wall was necessary to be calculated for calculation of concentrations in enzymatic reaction.
Volume of B. subtilis is 2.79μm³ and the thickness of cell wall is 35nm [5]. In order to approximate the cell wall volume assume that B. subtilis is a sphere - not a rod. Calculate the outer radius from the total volume: 0.874μm. Now subtract the thickness of cell wall from outer radius to determine inner radius of the sphere: 0.839μm. The volume of cell wall equals to the difference between outer volume and the inner volume (calculated from inner radius): cell wall volume=0.32×10^-15m³

5. Control volume selection

Note that product of the enzymatic reaction, AIP, is allowed to diffuse outside the cell. Hence, it is important to take into account the cell boundaries. It is worth considering whether diffusion or fluid movements will play a significant role.

Initially, we defined a control volume assuming that bacteria would grow in close colonies on the plate. We realized that our initial choice of control volume was not accurate, since our bacteria are meant to be used in suspension so we had to reconsider this issue.

This control volume is considered to be wrong, but the details were kept for reference.

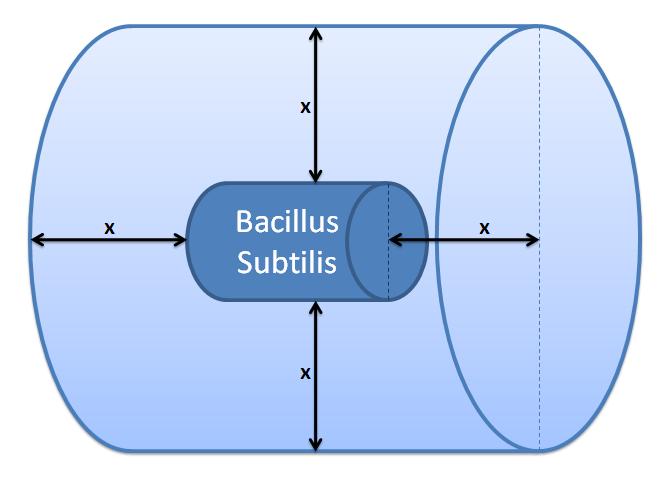
Initial Choice of Control Volume

Control volume initial choice
The control volume: The inner boundary is determined by the bacterial cell (proteins after being displayed and cleaved cannot diffuse back into bacterium). The outer boundary is more time scale dependent. We have assumed that after mass cleavage of the display-proteins by TEV, many of these AIPs will bind to the receptors quite quickly (eg. 8 seconds). Our volume is determined by the distance that AIPs could travel outwards by diffusion within that short time. In this way, we are sure that the concentration of AIPs outside our control volume after a given time is approximately 0. This approach is not very accurate and can lead us to false negative conclusions (as in reality there will be a concentration gradient, with highest concentration on the cell wall).

Control volume (Volume of B.sub to be excluded.
x indicates the distance travelled by AIPs from
the surface in time t).

Difussion distance was calculated using Fick's 1st Law: x=√2Dt, where: x - diffusion distance, D - diffusion constant, t - time of diffusion
D_average = 10.7×10^-11 m²s^-1 for a protein in agarose gel for pH=5.6 [3]
t = 8s (arbitrarily chosen)
This gives: x = 4.14×10^-5m
The control volume can be calculated by adding 2x to the length and the diamter of the cell.
This gives a control volume (CV) = 4.81×10^-7m³

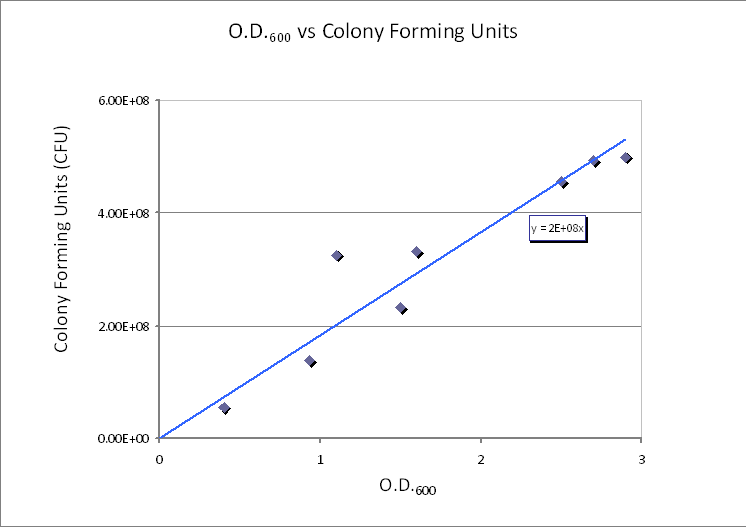
Using CFU to estimate the spacing between cells
CFU stands for Colony-forming unit. It is a measure of bacterial numbers. For liquids, CFU is measured per ml. We already have data of CFU/ml from the Imperial iGEM 2008 team, so we could use this data to estimate the number of cells in a given volume using a spectrometer at 600nm wavelength. The graph below is taken from the Imperial iGEM 2008 Wiki page [4].

CFU/ml vs. Optical Density at 600nm (OD600).

The graph shows values of CFU/ml for different optical densities. The range of CFU/ml is therefore between 0.5×10⁸ - 5×10⁸.
In this calculation, we assumed that only one cell will grow and become one colony (i.e. no more than one cell will form no more than one colony). Therefore, the maximum number of cells in 1ml of solution is 5×10⁸. Taking the volume of 1 ml = 10^-3 dm³ and dividing by the (maximum) number of cells in 1ml gives the average control volume (CV) around each cell: 2×10^-12 dm³/cell. For simplicity, we choose the control volume to be cubic. Taking the third root of this value gives the length of each side of the control volume.

Side length of cubic Control volume is y = 1.26×10^-4 dm = 1.26×10^-5 m.

Choice of Control Volume allows simplifications

Firstly, assume that the cells will be placed in the centre of the CV. Hence, after cleavage the protein will have an average distance of y/2 to travel in order to cross the boundary of the CV. Even if bacterium was not in the centre of CV and AIP had to diffuse across distance y, this is calculated using simplified 1 dimensional Fick's Law to happen within 0.01 ms. Hence, it will be almost instantaneous event for the concentration of AIPs around the cell to be uniform. Noticing that these time values are very small, we can approximate our model to have a uniform concentration across the volume. Since we are underestimating the value of AIP concentration right next to the cell's surface, we are overestimating the time required for the AIP concentration to reach the threshold level.
We can neglect the diffusive fluxes across the CV border (see figure below). Assuming that adjacent cells are producing the peptide at the same rate and that the concentration of TEV is the same around the cell, then the fluxes should be of the same value giving a net flux of zero. Hence, we can neglect diffusion and have our model limited to one bacterium.

Figure showing two cells with their control volumes.

6. Localised concentrations

It was realised that, for our choice of control volume, the system would be unlikely to perform well due to the high concentration levels of TEV or Schistosoma proteases that would be required. Hence, it was deduced that localised concentrations will play an important role in this model.
It was arbitrarily chosen that 20% to 50% of AIPs will bind to receptors rather than diffuse away. There are several arguments that would suggest this kind of percentage:

AIPs being very close to the cell surface will have an equal probability of heading back towards the bacterium as diffusing away from it (since the cell is a lot bigger than the AIPs).
It is likely that there will be some chemical interactions between AIPs and the bacterium that could be attracting the AIPs to the host bacterium (e.g. electrostatic attraction could be possible).

The percentage coefficient scales the AIP concentrations at the very end - after the ODE equations have been solved.

7. Protein production

This paper mentions that each cell displays 2.4×10⁵ peptides. [2]
2.4×10⁵ molecules = 2.4×10⁵/6.02×10²³ mol = 0.398671×10^-18 mol
Volume of B.sub cell wall: 0.32×10^-15m³
Concentration = [mol/L]
c = 1.24×10^-3 mol/L. This is the concentration of protein that will be displayed on a single cell of B.sub.

Hence, we can deduce that the final concentration that the protein expression will tend to is: c = 1.24×10^-3 mol/dm³ = c_final.

Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards c_final. The degradation rate was kept constant (same as used in output amplification module), and the production rate was adjusted match the final concentration to be achieved.
Using a similar model to the simple production of Dioxygenase for the Output Amplification Model (Model preA), we obtain the following graph:

Production of protein by transcription and translation.

References

Havarstein, L., Coomaraswamy, G. & Morrison, D. (1995) An unmodified heptadecapeptide pheromone induces competence for genetic transformation in Streptococcus pneumoniae. Proc. Natl. [Online] 92, 11140-11144. Available from: http://ukpmc.ac.uk/backend/ptpmcrender.cgi?accid=PMC40587&blobtype=pdf [Accessed 27th August 2010]
Kobayashi, G. et al (2000) Accumulation of an artificial cell wall-binding lipase by Bacillus subtilis wprA and/or sigD mutants. FEMS Microbiology Letters. [Online] 188(2000), 165-169. Available from: http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09188.x/pdf [Accessed 27th August 2010]
Gutenwik, J., Nilsson, B. & Axelsson, A. (2003) Determination of protein diffusion coefficients in agarose gel with a diffusion cell. Biochemical Engineering Journal. [Online] 19(2004), 1-7. Available from: http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6V5N-4B3MXDC-2-K&_cdi=5791&_user=217827&_pii=S1369703X03002377&_origin=search&_coverDate=07%2F01%2F2004&_sk=999809998&view=c&wchp=dGLzVtb-zSkzS&md5=c17d0e7320f03931006f9b1a10a438b9&ie=/sdarticle.pdf [Accessed August 20th 2010]
Imperial College London (2008) Biofabricator Subtilis - Designer Genes. [Online] Available from: https://2008.igem.org/Imperial_College/18_September_2008 [Accessed 1st September 2010]
Graham L. L. & Beverisge T. J. (1993) Structural Differentiation of the Bacillus subtilis 168 Cell Wall. Journal of Bacteriolofy. [Online] 5(1994), 1413-1420. Available from: http://jb.asm.org/cgi/reprint/176/5/1413?ijkey=27dafbac7e23dee50390d3fe67d9d1bab0c6f48c [Accessed October 26th 2010]

@@ Line 147: / Line 147: @@
 <h2>6. Localised concentrations</h2>
-It was realised that for above choice of control volume the system would be unlikely to perform due to high concentration levels of TEV or Schistosoma proteases that would have been required. Hence, it was deduced that localised concentrations will play important role in this model.
+It was realised that, for our choice of control volume, the system would be unlikely to perform well due to the high concentration levels of TEV or Schistosoma proteases that would be required. Hence, it was deduced that localised concentrations will play an important role in this model.
 <br/>
-It was arbitrarily chosen that 20% to 50% of AIPs will bind to receptors rather than diffuse away. There is several arguments that would suggest this kind of percentage:
+It was arbitrarily chosen that 20% to 50% of AIPs will bind to receptors rather than diffuse away. There are several arguments that would suggest this kind of percentage:
-<ul><li> AIP being very close to cell surface will have equal chances of heading back towards bacterium as diffusing away from it as cell is way bigger than they are.</li>
+<ul><li> AIPs being very close to the cell surface will have an equal probability of heading back towards the bacterium as diffusing away from it (since the cell is a lot bigger than the AIPs).</li>
-<li>It is likely that there will be some chemical interactions between AIP and bacterium that could be attracting AIP to the host bacterium. Eg. electrostatic attraction is possible.</li>
+<li>It is likely that there will be some chemical interactions between AIPs and the bacterium that could be attracting the AIPs to the host bacterium (e.g. electrostatic attraction could be possible).</li>
 </ul>
-The percentage coefficient scales the AIP concentrations at the very end - after the ODE equations have been solved
+The percentage coefficient scales the AIP concentrations at the very end - after the ODE equations have been solved.
 <h2>7. Protein production</h2>
 <ul>
-<li>The paper mentions that each cell displays 2.4&times;10<sup>5</sup> peptides. <a href="http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09188.x/pdf">[2]</a></li>
+<li>This paper mentions that each cell displays 2.4&times;10<sup>5</sup> peptides. <a href="http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09188.x/pdf">[2]</a></li>
 <li>2.4&times;10<sup>5</sup> molecules = 2.4&times;10<sup>5</sup>/6.02&times;10<sup>23</sup> mol = 0.398671&times;10<sup>-18</sup> mol</li>
 <li>Volume of B.sub cell wall: 0.32&times;10<sup>-15</sup>m<sup>3</sup></li>