Team:Peking/Modeling/Analysis
From 2010.igem.org
Evamonlight (Talk | contribs) (→Mechanisms of Minimal Semilog Networks and Key Parameters Analysis) |
Evamonlight (Talk | contribs) (→Motif Combinations that Improve IOA) |
||
| (23 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
{{:Team:Peking/Headermodel}} | {{:Team:Peking/Headermodel}} | ||
{{:Team:Peking/boxes}} | {{:Team:Peking/boxes}} | ||
| Line 9: | Line 10: | ||
<br><br> | <br><br> | ||
<font size=6><font color=#585858><font face="Franklin Gothic Demi Cond"> Analyses and Results</font></font></font> | <font size=6><font color=#585858><font face="Franklin Gothic Demi Cond"> Analyses and Results</font></font></font> | ||
| - | <br><br> | + | <br><br><br> </html> |
| + | [[Team:Peking/Modeling|Modeling]] > [[Team:Peking/Modeling/Analysis|Analysis and Results]] <html> | ||
</div> | </div> | ||
| Line 15: | Line 17: | ||
<div id="middlewhite"> | <div id="middlewhite"> | ||
</html> | </html> | ||
| - | + | We get the value of the characters (r mainly) after calculation under each set of parameters, then we analyze them trying to find one simple topology that can function well. | |
| - | We get the value of the characters (r mainly) after calculation under each set of parameters, then we | + | |
==Identifying Minimal IOA Networks== | ==Identifying Minimal IOA Networks== | ||
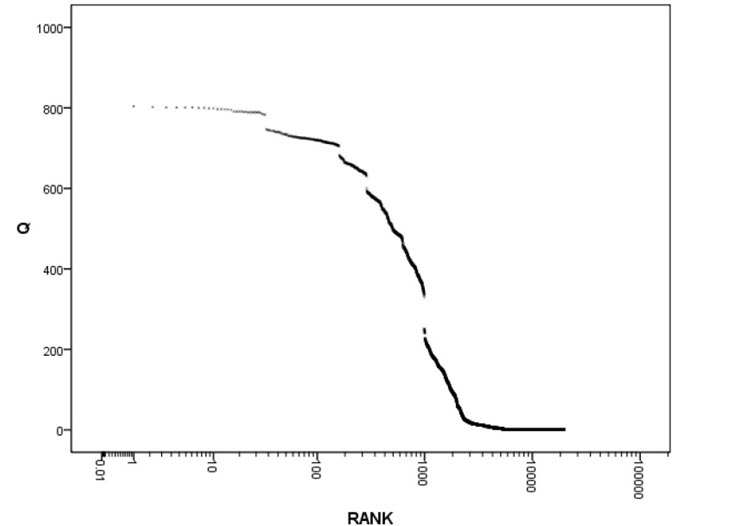
| - | Here we define Q value as the number of IOA function circuit among 10000 sets of network parameters, and it indicates the robustness of one topology to finish the IOA function—the larger Q value is, the more robust the topology is. We sort in reverse sequence all the network topologies according to their Q value and the x axis is their rank( Figure 6).We can observe that most network topologies have 0 or low Q value while there’s only a small part of the topologies having large Q value.<br> | + | Here we define Q value as the number of IOA function circuit among 10000 sets of network parameters, and it indicates the robustness of one topology to finish the IOA function—the larger Q value is, the more robust the topology is. We sort in reverse sequence all the network topologies according to their Q value and the x axis is their rank( Figure 6).We can observe that most network topologies have 0 or low Q value while there’s only a small part of the topologies having large Q value.<br><br> |
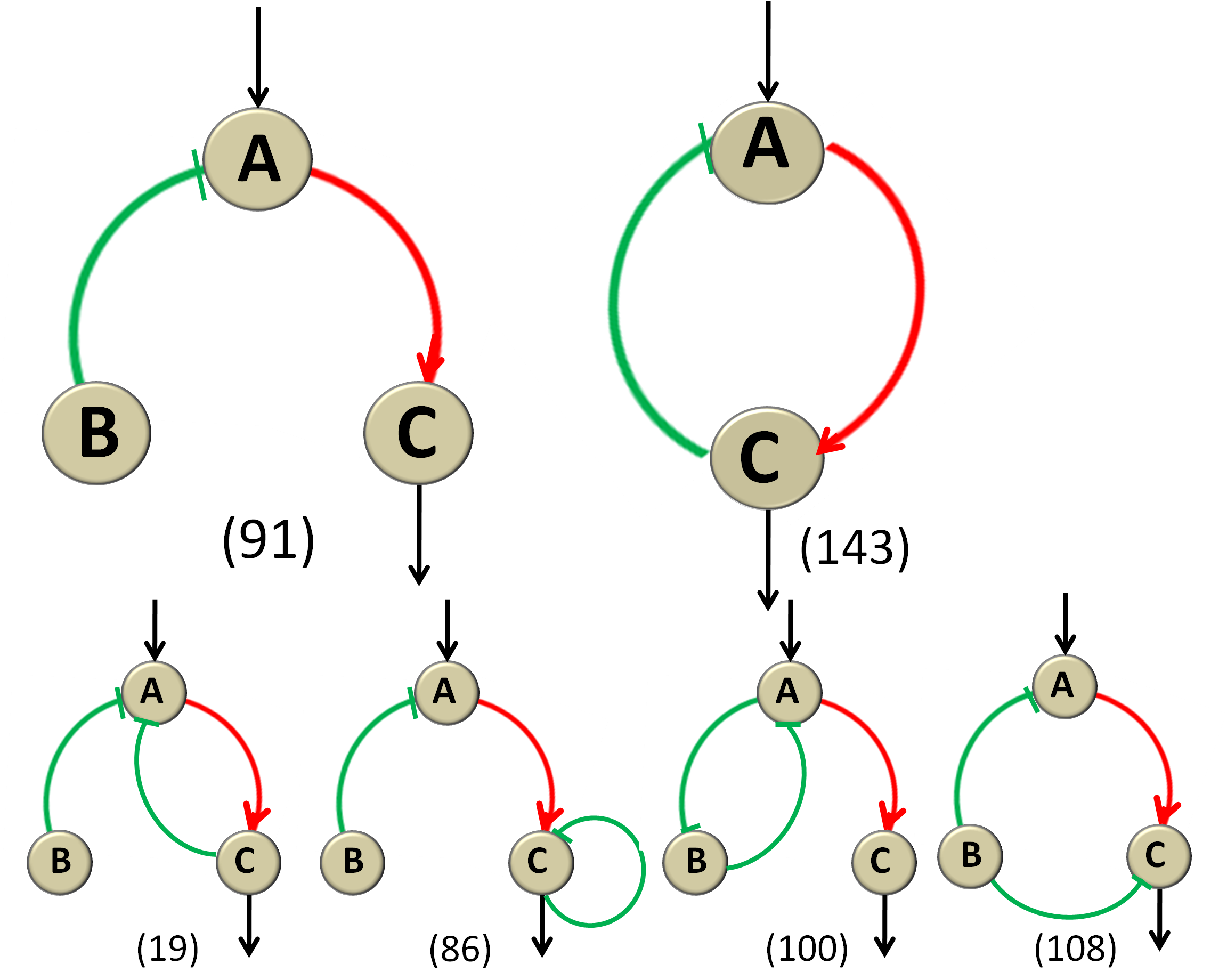
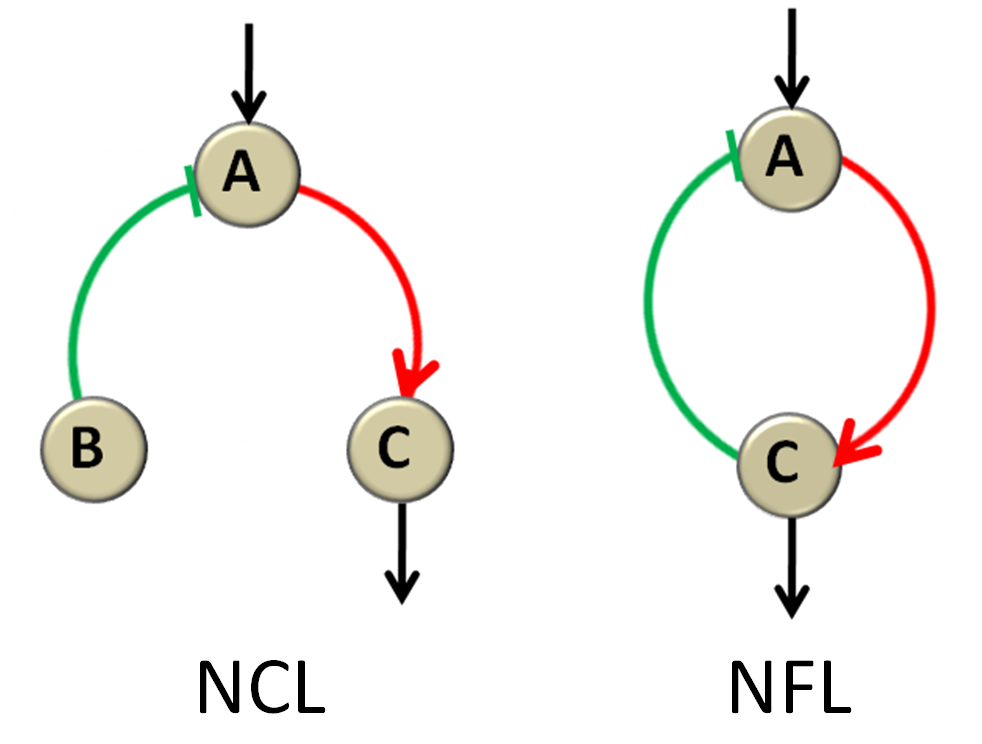
| - | We firstly | + | We firstly analyze the first 160 network topologies ( Q >=705 ) and list in Figure 7 all the simplest topologies that have only 3 or less direct links between the three nodes.( Figure 7) Among the 14 topologies, there are 12 three-link networks and 2 two-node networks so that we can see that the minimal number of links for the topologies to be functional is two but the most usual number is 13. The common features of the networks capable of IOA are either one negative control loop (NCL) or one negative feedback loop (NFL). Here we define NCL as a topology that has one negative control on the input-receiving node (A) from the intermediate node (B) and one positive regulation on the output node (C) from A node.(as the 1st topology in Figure 7 and the 1st one in Figure 8) Similarly we define NFL as a topology that share the positive-regulation link from A to C, while uniquely have one negative feedback from C to A.(as the 2nd topology in Figure 7 and the 2nd one in Figure 8) And the NCL topology seemingly more robust than the NFL topology, as there are 9 topologies out of the 14 simplest networks contain NCL topology compared to 6 of NFL, so that B node appears to be important, which will be discussed in details in the following part. |
<br> | <br> | ||
[[Image:Qlinear.jpg|350px|center]] | [[Image:Qlinear.jpg|350px|center]] | ||
| Line 46: | Line 47: | ||
[[Image:NFunction51.png]] | [[Image:NFunction51.png]] | ||
<br><br> | <br><br> | ||
| - | Because | + | Because [[Image:0001.png]] is constant, the coefficient of I is also constant. So there comes the linear correlation between [[Image:0000.png]](output concentration) and I.<br><br> |
When [[Image:NFunction41.png]] ,<br> | When [[Image:NFunction41.png]] ,<br> | ||
[[Image:NFunction61.png]] | [[Image:NFunction61.png]] | ||
<br><br> | <br><br> | ||
| - | And the concentration of B node is actually part of the slope coefficient the linear equation, we can imagine that the function of B node is to lower the concentration of A straightly without the interference of other factors as well as control the concentration of A more precisely and more freely to make the parameter restriction easier to achieve and at the same time the output range is not too small. As we know, the stochastic error may make vague the linear relationship when the values of y axis are too near. The lower concentration | + | And the concentration of B node is actually part of the slope coefficient the linear equation, we can imagine that the function of B node is to lower the concentration of A straightly without the interference of other factors as well as control the concentration of A more precisely and more freely to make the parameter restriction easier to achieve and at the same time the output range is not too small. As we know, the stochastic error may make vague the linear relationship when the values of y axis are too near. The lower concentration [[Image:0002.png]] is, the steeper the line is, and so the bigger the range is, which in biology means that the bioreporter is more sensitive to certain environmental signal. Through modifying the parameters of node B, we can get a proper concentration of A node to achieve a good r. In all, the node B is a proportion node.<br> |
===NFL Topology=== | ===NFL Topology=== | ||
| Line 72: | Line 73: | ||
<br><br> | <br><br> | ||
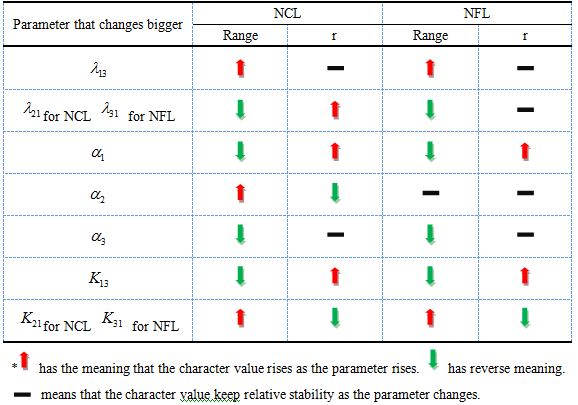
<html><font size=1.5><b> Table 2 The change of two important characters as the parameters rise</b></font></html> | <html><font size=1.5><b> Table 2 The change of two important characters as the parameters rise</b></font></html> | ||
| - | [[Image: | + | [[Image:Table2222.png|center]] |
[[https://2010.igem.org/Team:Peking/Modeling TOP]] | [[https://2010.igem.org/Team:Peking/Modeling TOP]] | ||
| Line 85: | Line 86: | ||
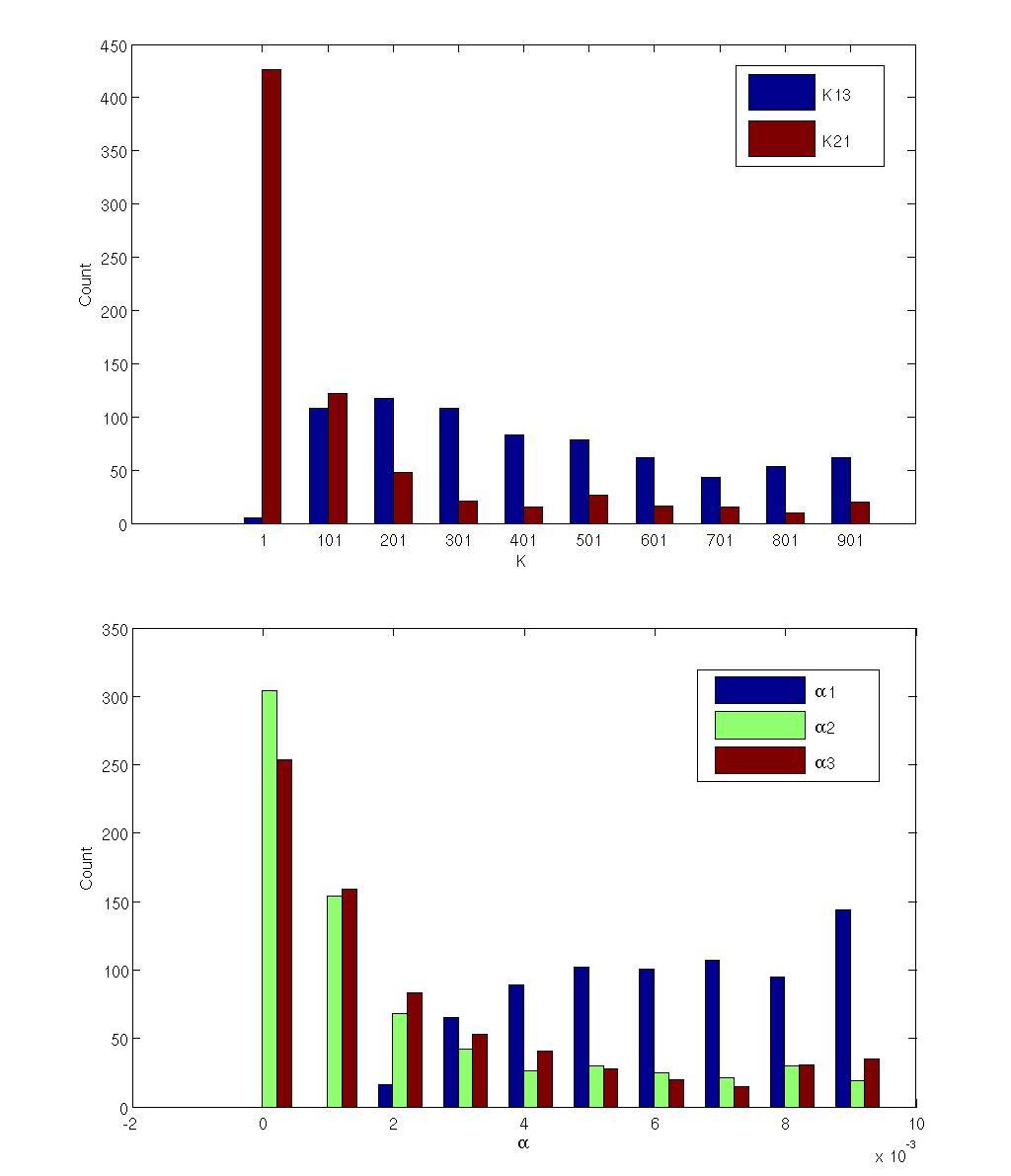
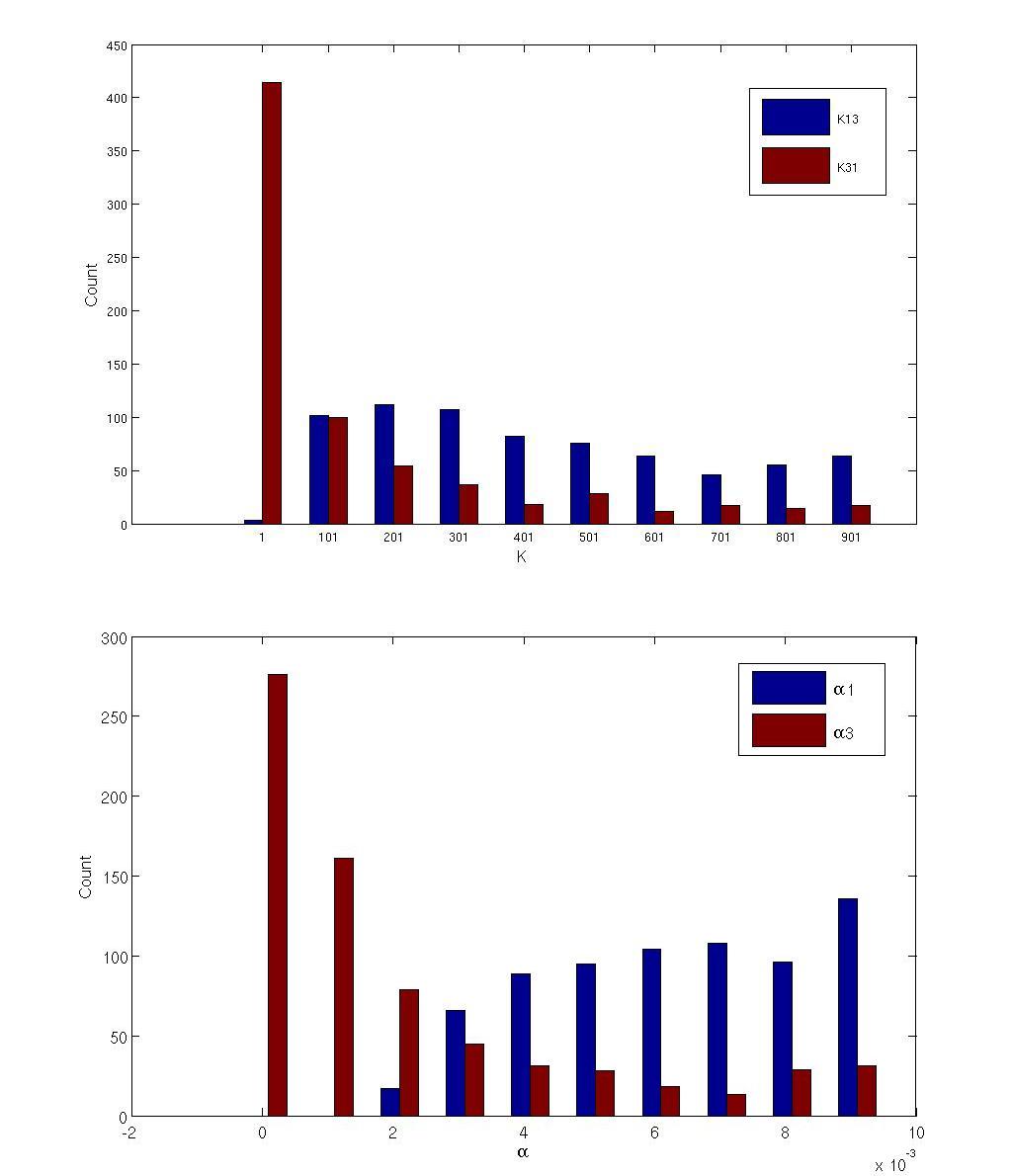
<html><font size=1.5><b><center>Figure 11 Distribution of NFL topology parameters which can establish linear response curves.</center></b><br></font></html> | <html><font size=1.5><b><center>Figure 11 Distribution of NFL topology parameters which can establish linear response curves.</center></b><br></font></html> | ||
| - | It can be seen that the constant K of the repression ( | + | It can be seen that the constant K of the repression ([[Image:006.png]] and [[Image:007.png]]) are generally lower compared to [[Image:005.png]], which means that there should be an intense repression on node A. Such a result also fits well with the condition[[Image:NFunction41.png]] used in the derivation above.<br><br> |
We also notice that the degradation rates, α, of the nodes also show apparent tendency. The degradation rate of the node A is generally higher, while the repressing nodes (B or C) have lower degradation rates. Such a tendency also shows that the repression on node A should be intense in order to establish a more linear response curve between input and output.<br> | We also notice that the degradation rates, α, of the nodes also show apparent tendency. The degradation rate of the node A is generally higher, while the repressing nodes (B or C) have lower degradation rates. Such a tendency also shows that the repression on node A should be intense in order to establish a more linear response curve between input and output.<br> | ||
| Line 91: | Line 92: | ||
==Analysis of All Possible Three-Node Networks== | ==Analysis of All Possible Three-Node Networks== | ||
| - | The above analyses focused on minimal( less than or equal to 3 links) three-node networks and identified simple topologies that are sufficient for IOA function, also unraveling the mechanism that the topologies work. But whether the topologies are necessary for the IOA function is not understood yet. In other words, are the identified minimal topologies the foundation of all possible networks, or are there more complex higher-order solutions that do not contain these minimal topologies? To answer the questions above, we | + | The above analyses focused on minimal( less than or equal to 3 links) three-node networks and identified simple topologies that are sufficient for IOA function, also unraveling the mechanism that the topologies work. But whether the topologies are necessary for the IOA function is not understood yet. In other words, are the identified minimal topologies the foundation of all possible networks, or are there more complex higher-order solutions that do not contain these minimal topologies? To answer the questions above, we analyze the first 160 topologies (Q>705) that are well capable of the IOA function.(Figure 12)<br> |
[[Image:WenshiLINEAR.png|300px|center]] | [[Image:WenshiLINEAR.png|300px|center]] | ||
<br> | <br> | ||
<html><font size=1.5><b>Figure 12 Analysis of the first 160 networks</b> We count all the NCLs and NFLs and also the IOA networks, and discover that all of the IOA networks can be classified into NCL/NFL/the combination of the two. And there are more IOA functional network featured in NCL than those characterized with NFL.<br></font></html> | <html><font size=1.5><b>Figure 12 Analysis of the first 160 networks</b> We count all the NCLs and NFLs and also the IOA networks, and discover that all of the IOA networks can be classified into NCL/NFL/the combination of the two. And there are more IOA functional network featured in NCL than those characterized with NFL.<br></font></html> | ||
<br> | <br> | ||
| - | Analysis of these robust topologies shows that they are overrepresented with NCL and NFL. All 160 topologies contain at least one NCL or NFL motif ( or both ). These results indicate that at least one of these motifs is necessary for IOA function. <br> | + | Analysis of these robust topologies shows that they are overrepresented with NCL and NFL. All 160 topologies contain at least one NCL or NFL motif ( or both ). These results indicate that at least one of these motifs is necessary for IOA function. <br><br> |
Supplementarily, the NCL average Q value(AQV)of all 19683 topologies is 17.14 while the NFL AQV is only 9.36, which again indicate that the NCL is more robust than NFL that have drew conclusion in the minimal topology analysis. | Supplementarily, the NCL average Q value(AQV)of all 19683 topologies is 17.14 while the NFL AQV is only 9.36, which again indicate that the NCL is more robust than NFL that have drew conclusion in the minimal topology analysis. | ||
<br> | <br> | ||
| Line 105: | Line 106: | ||
[[Image:JuleiLINEAR.png|400px|center]] | [[Image:JuleiLINEAR.png|400px|center]] | ||
<br> | <br> | ||
| - | <html><font size=1.5><b>Figure 13 The clustergrams of the networks</b>We use the clustergram command in matlab to get the additional features of the functional networks. The nine vertical rectangle bar stand for nine links in Figure 2 which are, respectively, from A to A, from A to B, from A to C, from B to A, from B to B, from B to C, from C to A, from C to B, from C to C. And red stands for activation, green for repression and black for no regulation. The topologies on the right are corresponding minimal topologies that is shown in the clustergrams on the left.<br></font></html> | + | <html><font size=1.5><b>Figure 13 The clustergrams of the networks</b>We use the clustergram command in matlab to get the additional features of the functional networks. The nine vertical rectangle bar stand for nine links in Figure 2 which are, respectively, from A to A, from A to B, from A to C, from B to A, from B to B, from B to C, from C to A, from C to B, from C to C. And red stands for activation, green for repression and black for no regulation. The topologies on the right are corresponding minimal topologies that is shown in the clustergrams on the left.<br></font></html><br> |
The results clearly indicate that apart from the link from A to C, there should be no positive regulation, and the NFL topology hates the link from A to A, while the combination topologies show no additional tendency.<br> | The results clearly indicate that apart from the link from A to C, there should be no positive regulation, and the NFL topology hates the link from A to A, while the combination topologies show no additional tendency.<br> | ||
[[https://2010.igem.org/Team:Peking/Modeling TOP]] | [[https://2010.igem.org/Team:Peking/Modeling TOP]] | ||
| Line 114: | Line 115: | ||
[[https://2010.igem.org/Team:Peking/Modeling TOP]] | [[https://2010.igem.org/Team:Peking/Modeling TOP]] | ||
| - | + | <html> | |
| - | + | </div> | |
| - | + | <div id="bottomwhite"> | |
| - | + | <a href="#top"><img src="https://static.igem.org/mediawiki/2010/8/87/Top.png" width="100px" height="75px"alt="go back to top"></a> | |
| - | + | </div> | |
| - | + | </html> | |
| - | + | ||
| - | + | ||
| - | < | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | == | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | < | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
Latest revision as of 11:39, 27 October 2010

Identifying Minimal IOA Networks
Here we define Q value as the number of IOA function circuit among 10000 sets of network parameters, and it indicates the robustness of one topology to finish the IOA function—the larger Q value is, the more robust the topology is. We sort in reverse sequence all the network topologies according to their Q value and the x axis is their rank( Figure 6).We can observe that most network topologies have 0 or low Q value while there’s only a small part of the topologies having large Q value.
We firstly analyze the first 160 network topologies ( Q >=705 ) and list in Figure 7 all the simplest topologies that have only 3 or less direct links between the three nodes.( Figure 7) Among the 14 topologies, there are 12 three-link networks and 2 two-node networks so that we can see that the minimal number of links for the topologies to be functional is two but the most usual number is 13. The common features of the networks capable of IOA are either one negative control loop (NCL) or one negative feedback loop (NFL). Here we define NCL as a topology that has one negative control on the input-receiving node (A) from the intermediate node (B) and one positive regulation on the output node (C) from A node.(as the 1st topology in Figure 7 and the 1st one in Figure 8) Similarly we define NFL as a topology that share the positive-regulation link from A to C, while uniquely have one negative feedback from C to A.(as the 2nd topology in Figure 7 and the 2nd one in Figure 8) And the NCL topology seemingly more robust than the NFL topology, as there are 9 topologies out of the 14 simplest networks contain NCL topology compared to 6 of NFL, so that B node appears to be important, which will be discussed in details in the following part.
Figure 6 The Q value network topologies SequenceWe sort in reverse sequence all the network topologies according to their Q value. X Axis is their ranks, while Y Axis is their corresponding Q values. The figure indicates that most network topologies have 0 or low Q value while there’s only a small part of the topologies having large Q value.
Figure 7 All Functional NetworksThe numbers below each network are their ranks. The two bigger topologies have 2 links while the other 12 networks have 3 links. In each network, the green arc with one short straight line at one end stands for repression from the start node to the end node and the red arc with one arrow at one end stands for activation.
Figure 8 The NCL and NFL topologyThe green and red line have the same meaning as in Figure 7.
[TOP]
Mechanisms of Minimal IOA Networks and Key Parameters Analysis
Aimed at answering the question why the two topologies defined above (Figure 8) is functional in IOA, we unravel their mechanisms using the ODE equations in this part, also getting the parameter restrictions of each topology.
NCL Topology
When the network has built steady state:
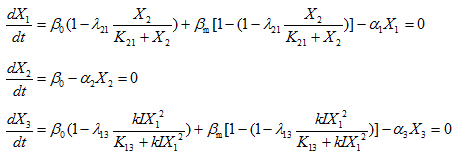
Solve the equations:
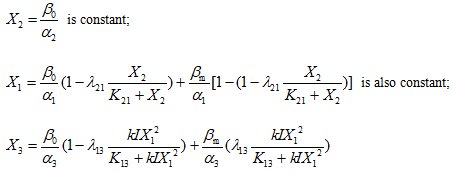
If there is ![]() , then
, then
![]()
Because ![]() is constant, the coefficient of I is also constant. So there comes the linear correlation between
is constant, the coefficient of I is also constant. So there comes the linear correlation between ![]() (output concentration) and I.
(output concentration) and I.
When ![]() ,
,
![]()
And the concentration of B node is actually part of the slope coefficient the linear equation, we can imagine that the function of B node is to lower the concentration of A straightly without the interference of other factors as well as control the concentration of A more precisely and more freely to make the parameter restriction easier to achieve and at the same time the output range is not too small. As we know, the stochastic error may make vague the linear relationship when the values of y axis are too near. The lower concentration ![]() is, the steeper the line is, and so the bigger the range is, which in biology means that the bioreporter is more sensitive to certain environmental signal. Through modifying the parameters of node B, we can get a proper concentration of A node to achieve a good r. In all, the node B is a proportion node.
is, the steeper the line is, and so the bigger the range is, which in biology means that the bioreporter is more sensitive to certain environmental signal. Through modifying the parameters of node B, we can get a proper concentration of A node to achieve a good r. In all, the node B is a proportion node.
NFL Topology
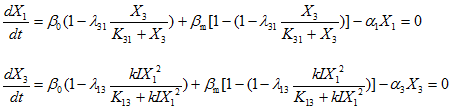
Also solve the equations:
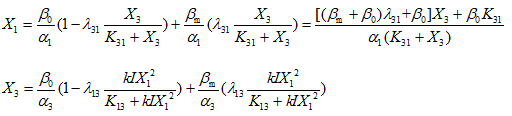
If![]() ,then
,then![]() is constant;
is constant;
And if![]() ,then
,then![]() ,which correlation is the same as the NCL Topology.
,which correlation is the same as the NCL Topology.
Compare X1 here with the concentration of node A in NCL topology, one can easily discover that X1 here is higher and more dull, which makes it more hard to get a balance between satisfying the second parameter restriction and the need for the range to be rational. Then we can understand why NFL topology is less than NCL in high-Q-value topologies.
Key Parameter Analysis
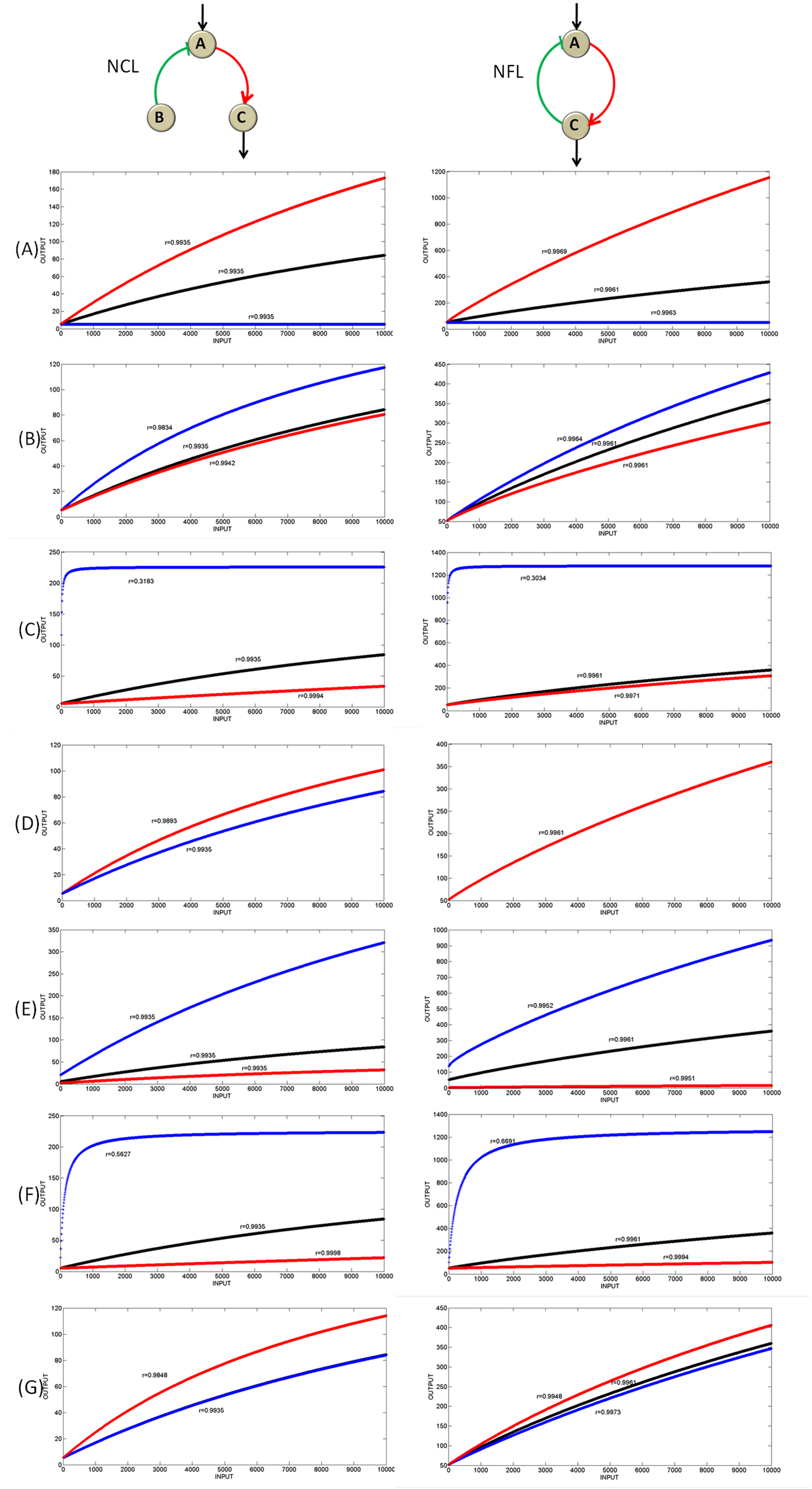
Aimed at unraveling the relative importance among parameters, we got all functional sets of parameters of NCL&NFL and selected randomly one set, respectively, from the two topologies and processed them with Matlab to compare the differences once the parameters change. The results are in Figure 9. From changes of the two important characters – the output range and r with the change of parameters (Table 2), we got the answer to previous questions.
Figure 9 Analysis for key parametersWe got all functional sets of parameters of NCL&NFL and selected randomly one set, respectively, from the two topologies and processed them with Matlab to compare the differences once the parameters change. When analyzing one parameter, we only change this very parameter and keep others the same, and when we change the parameter to a lower level, we get the blue line, when to a higher level, we get the red line and the black line is for the unchanged parameter set. Each line has its Pearson Correlation Coefficient r marked in the figure. The X Axis is the concentration of Hg ion as INPUT whose range is 1 to 10000 nM, and the Y Axis is the concentration of node C with the unit of nM.(A) We analyze  for both topologies. (B)
for both topologies. (B) for NCL and
for NCL and for NFL (C) The degradation rate of A (
for NFL (C) The degradation rate of A ( )for both topologies (D) The degradation rate of B(
)for both topologies (D) The degradation rate of B(  )for both (E)The degradation rate of C(
)for both (E)The degradation rate of C( ) for both (F) The dissociation rate of A to the binding site on the gene of C(
) for both (F) The dissociation rate of A to the binding site on the gene of C(  ) for both (G)
) for both (G) for NCL and
for NCL and for NFL.
for NFL.
For NCL, the degradation rate of A (![]() ) and the value of Kd from node A to node C (
) and the value of Kd from node A to node C ( ![]() ) are relatively more important to r, and the degradation rate of C (
) are relatively more important to r, and the degradation rate of C (![]() ) along with Kd from node A to node C (
) along with Kd from node A to node C ( ![]() ) are essential to the output range, while the constant indicating repression from B to A(
) are essential to the output range, while the constant indicating repression from B to A(![]() ) , the degradation rate of B (
) , the degradation rate of B (![]() ) as well as Kd from node B to node A (
) as well as Kd from node B to node A (![]() ) influence little both characters. From Table 2 and the analysis above, we can draw the conclusion that in practice, the parameter
) influence little both characters. From Table 2 and the analysis above, we can draw the conclusion that in practice, the parameter ![]() should be larger and
should be larger and ![]() should be as small as possible. While for NFL, the condition is similar. It is still
should be as small as possible. While for NFL, the condition is similar. It is still ![]() and
and ![]() that are important to r, but the key parameters on the output range are
that are important to r, but the key parameters on the output range are ![]()
![]()
![]()
![]() , more than the key parameters for output range for NCL. So the suggest to practice is still smaller
, more than the key parameters for output range for NCL. So the suggest to practice is still smaller ![]() and larger
and larger ![]() , what’s more, there should be smaller
, what’s more, there should be smaller ![]() for larger output range according to the character changes in Table 2.
for larger output range according to the character changes in Table 2.
Table 2 The change of two important characters as the parameters rise
[TOP]
Parameters Tendency of the IOA Networks
In order to test the correctness of our analysis about the key parameters, we look more closely at the parameters of the simplest IOA networks. For the two simplest networks in Figure 6, we examine the distribution of the parameter values which can realize linear response between input and output out of the total 10000 sets of parameters used in the search.(Figure10, Figure11)
It can be seen that the constant K of the repression (![]() and
and ![]() ) are generally lower compared to
) are generally lower compared to ![]() , which means that there should be an intense repression on node A. Such a result also fits well with the condition
, which means that there should be an intense repression on node A. Such a result also fits well with the condition![]() used in the derivation above.
used in the derivation above.
We also notice that the degradation rates, α, of the nodes also show apparent tendency. The degradation rate of the node A is generally higher, while the repressing nodes (B or C) have lower degradation rates. Such a tendency also shows that the repression on node A should be intense in order to establish a more linear response curve between input and output.
[TOP]
Analysis of All Possible Three-Node Networks
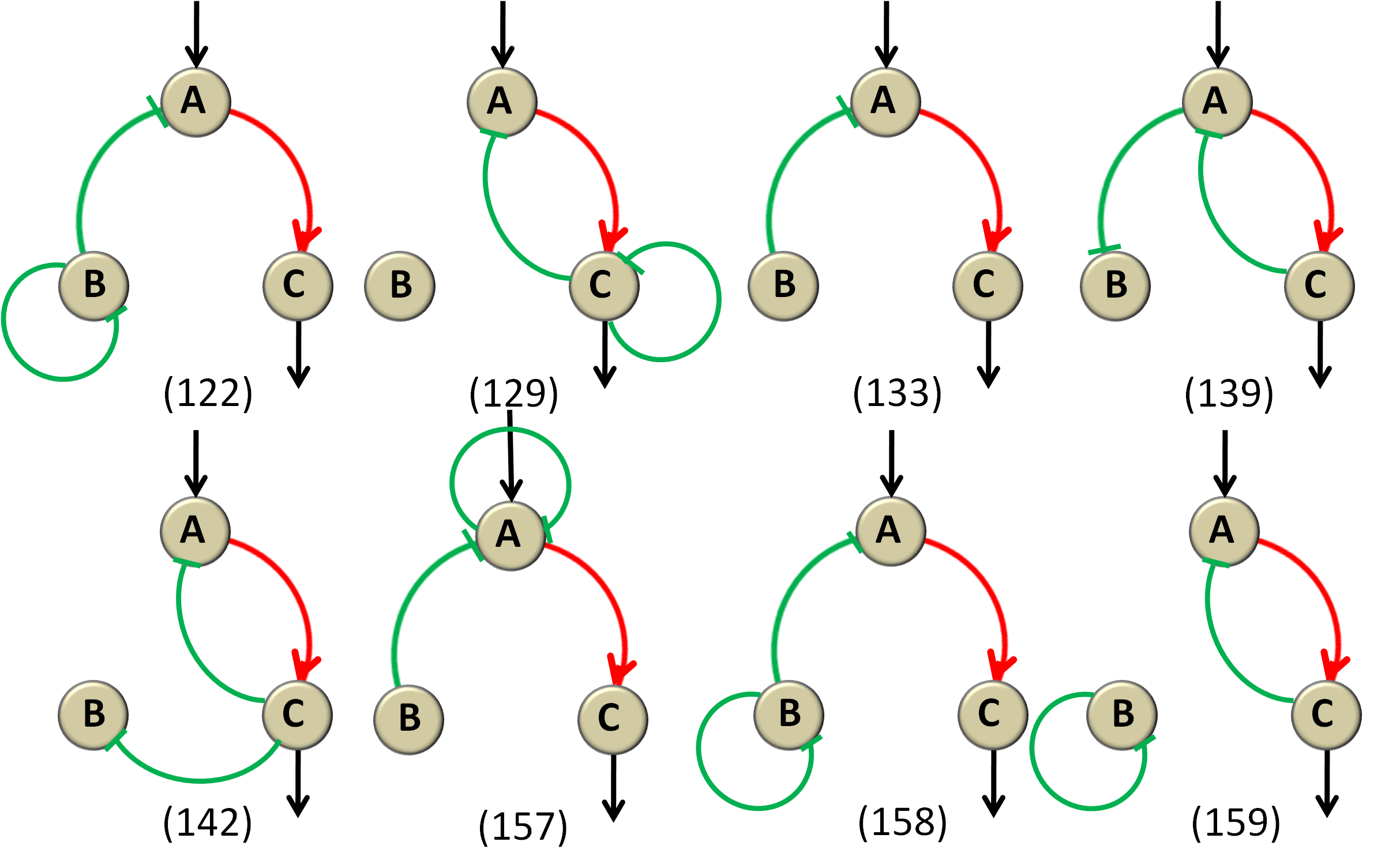
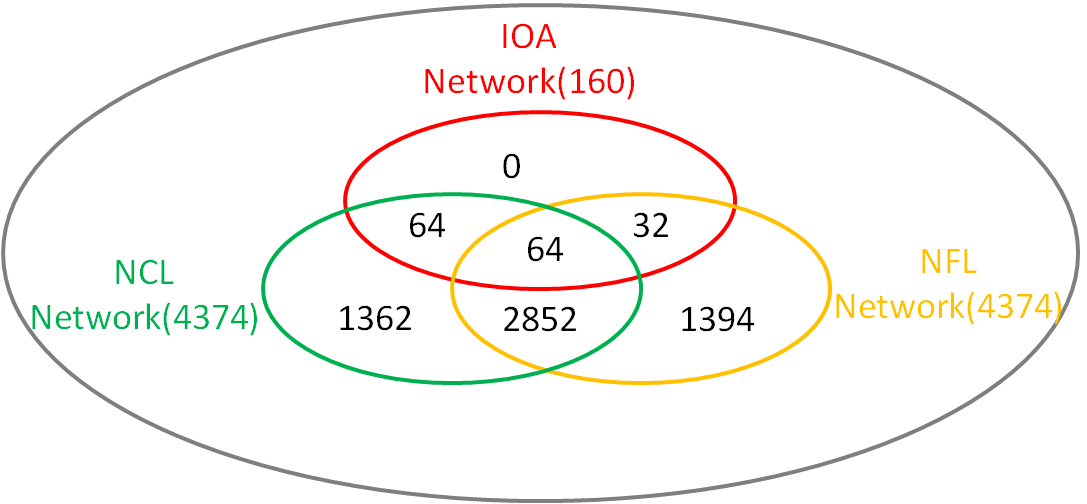
The above analyses focused on minimal( less than or equal to 3 links) three-node networks and identified simple topologies that are sufficient for IOA function, also unraveling the mechanism that the topologies work. But whether the topologies are necessary for the IOA function is not understood yet. In other words, are the identified minimal topologies the foundation of all possible networks, or are there more complex higher-order solutions that do not contain these minimal topologies? To answer the questions above, we analyze the first 160 topologies (Q>705) that are well capable of the IOA function.(Figure 12)
Figure 12 Analysis of the first 160 networks We count all the NCLs and NFLs and also the IOA networks, and discover that all of the IOA networks can be classified into NCL/NFL/the combination of the two. And there are more IOA functional network featured in NCL than those characterized with NFL.
Analysis of these robust topologies shows that they are overrepresented with NCL and NFL. All 160 topologies contain at least one NCL or NFL motif ( or both ). These results indicate that at least one of these motifs is necessary for IOA function.
Supplementarily, the NCL average Q value(AQV)of all 19683 topologies is 17.14 while the NFL AQV is only 9.36, which again indicate that the NCL is more robust than NFL that have drew conclusion in the minimal topology analysis.
[TOP]
Motif Combinations that Improve IOA
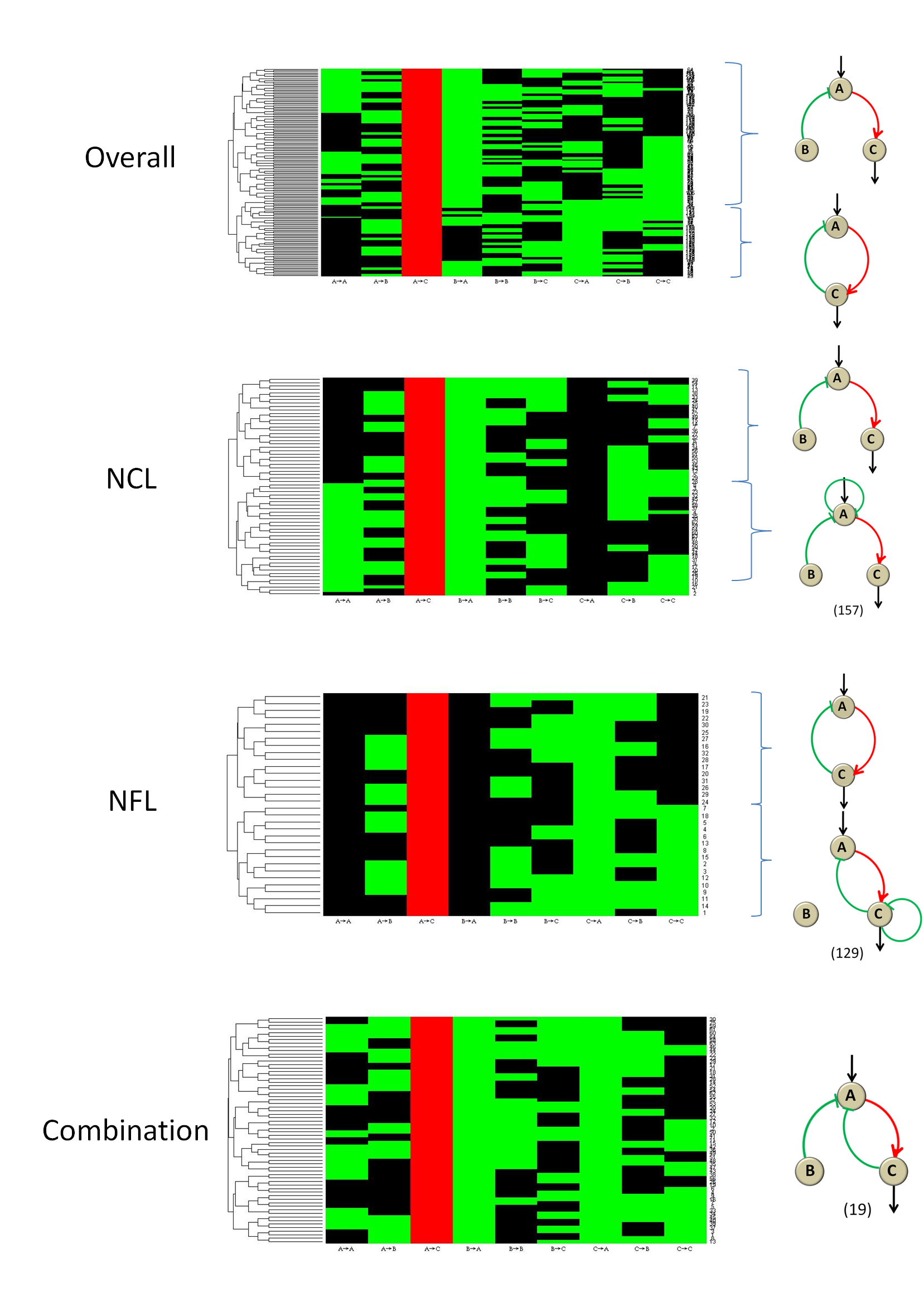
To investigate what additional features can improve the functional performance in some more complex and more robust networks than minimal topologies, we clustered the first 160 networks and then cluster them respectively in three categories: NCL, NFL and the combination of the two. (Figure 13)
Figure 13 The clustergrams of the networksWe use the clustergram command in matlab to get the additional features of the functional networks. The nine vertical rectangle bar stand for nine links in Figure 2 which are, respectively, from A to A, from A to B, from A to C, from B to A, from B to B, from B to C, from C to A, from C to B, from C to C. And red stands for activation, green for repression and black for no regulation. The topologies on the right are corresponding minimal topologies that is shown in the clustergrams on the left.
The results clearly indicate that apart from the link from A to C, there should be no positive regulation, and the NFL topology hates the link from A to A, while the combination topologies show no additional tendency.
[TOP]
Summary
In all, by exhaustively searching all network and analyzing the results, we draw the conclusion that NCL meets our need in application well, and we get the proper parameter range for practice.
[TOP]
 "
"