Team:Peking/Modeling

From 2010.igem.org

(Difference between revisions)
(→Introduction)
(→Introduction)
 
(39 intermediate revisions not shown)
Line 18: Line 18:
</html>
</html>
=Introduction=
=Introduction=
-
<html>
+
The biological systems are full of noises, and the response of bioreporters can be represented by a Hill Function. Noises will be significantly amplified and the output detected will be invalid at the ends of dose response curve.(Figure 1(a)) Therefore, The detection is limited at a narrow range. In order to solve the problem, we seek to transform the Hill Function curve to a straight line. As Figure 1(a) shows, the noise is reducted, and the sensitivity and detectable-range-characteristic of biosensors will be significantly improved.  <br><br>
-
<font color=#000000><font face="Verdana">
+
Aimed at finding a genetic circuit that can perform the transformation, a simple and universal one for practice convenience, we adopted the process of [[Team:Peking/Notebook/Vocabulary#Reverse engineering|Reverse engineering]] which in our work means to enumerate all possible networks and analyzed whether they function well, thus getting the right topology. In details, we first express the target functionalities in quantitative characters and set numerical standards according to our expectations, next define the network for simplest circuit search and derive equations precisely describing it, then calculate the characters using the equations and compare them with standards, then further analyze the comparison results and find the simplest functional network. Finally, to fully understand it and provide enough information for application, we analyze the mechanism and the parameter preferences, as well as exploring whether the very circuit is necessary for performing the function well.
-
We adopted the process of Reverse Engineering which in our work means to enumerate all possible network topologies and analyzed whether they fit the objection function or not, thus getting the right topology.
+
<br><br>
-
<br>
+
Here we name our target functionality as Input-Output Alignment(IOA). In order to define IOA precisely for need of calculation, we considered most important characters of IOA and adopted Pearson Correlation Coefficient r to represent Input-Output Linear Relationship in the overall search work ( when r>0.99 we consider the network topology having the IOA function ), and also, regulated two levels for the initial and ultimate output concentration for the second character – the output range in further search work.(Figure 1(b))
-
<br>
+
<br><br>
-
Here we chose the object function as Input-Output Alignment. In order to define IOA precisely for need of calculation, we considered most important characters of IOA and adopted Pearson Correlation Coefficient r to represent Input-Output Linear Relationship in the overall search work ( when r>0.99 we consider the network topology having the IOA function ), and also, regulated two levels for the initial and ultimate output concentration for the second character – the output range in further search work.(Figure 1)
+
<br>
<br>
 +
[[Image:Intro2.png|center|600px]]
<br>
<br>
-
<img src="https://static.igem.org/mediawiki/2010/9/98/Target_function.jpg" align=middle width="450">
 
<br>
<br>
-
<br>
+
<html>
-
<b><font size=1.5>Figure 1 Factors for selection of IOA network topologies.</b> r is the Pearson Correlation Coefficient and the output range is HIGHLEVEL minus LOWLEVEL.</font>
+
<font size=1.5><b>Figure 1</b> (a) The transformation reducts noises and make output more recognizable.(b)Factors for selection of IOA network topologies. r is the Pearson Correlation Coefficient and the output range is HIGHLEVEL minus LOWLEVEL.</font>  
-
</font></font>
+
</html>
</html>
=Calculating Process=
=Calculating Process=
<html>
<html>
-
<font size=3><font color=#000000><font face="Times New Roman">
 
In this part, we will demostrate our calculating process in three sections--Network enumeration, Equations set up and network topologies’ analysis.
In this part, we will demostrate our calculating process in three sections--Network enumeration, Equations set up and network topologies’ analysis.
<br>
<br>
-
<br>
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
<a href="https://2010.igem.org/Team:Peking/Modeling/CalculationProcess">== Learn more ==</a>
<a href="https://2010.igem.org/Team:Peking/Modeling/CalculationProcess">== Learn more ==</a>
-
</font></font></font>
+
 
</html>
</html>
=Analyses and Results=
=Analyses and Results=
<html>
<html>
-
<font size=3><font color=#000000><font face="Times New Roman">
+
Here we analyzed the results we obtained and found the final right topology.
-
As we search for proper network in two ways: linear and semilog, this part is divided into two sections -- linear and semilog.
+
<br>
<br>
-
 
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
-
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
+
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
<a href="https://2010.igem.org/Team:Peking/Modeling/Analysis">== Learn more ==</a>
<a href="https://2010.igem.org/Team:Peking/Modeling/Analysis">== Learn more ==</a>
 +
</html>
 +
 +
=Advanced Model=
 +
<html>
 +
When the range of input is very large, the IOA networks no longer meet out needs and so we tried to find one semilog-linear topology in this section.
 +
<br>
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
-
</font></font></font>
+
<a href="https://2010.igem.org/Team:Peking/Modeling/Advanced_Model">== Learn more ==</a>
</html>
</html>
=References=
=References=
<html>
<html>
-
 
+
1 Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K. & Walter, P. (2008). Molecular Biology of the Cell (Garland, New York).<br>
-
<font size=3><font color=#000000><font face="Times New Roman">
+
2 Nicolas E. Buchler, Ulrich Gerland, Terence Hwa (2005). Nonlinear protein degradation and the function of genetic circuits, PNAS 102, 9559-9564.<br>
-
1 Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K. & Walter, P. (2002)Molecular Biology of the Cell (Garland, New York).<br>
+
3 John D. Helmann, Barry T. Ballard, Christopher T. Walsh (1998). The MerR Metalloregulatory Protein Binds Mercuric Ion as a Tricoordinate, Metal-Bridged Dimer. Science 247, 946-948.<br>
-
2 Nicolas E. Buchler, Ulrich Gerland, Terence Hwa, Nonlinear protein degradation and the function of genetic circuits[J],PNAS,2005,102(27),9559-9564.<br>
+
4 Diana. M, Ralston and Thomas V. O Halloran (1990). Ultrasensitivity and heavy-metal selectivity of the allosterically modulated MerR transcription complex. PNAS 87, 3846-3850.<br>
-
3 John D. Helmann, Barry T. Ballard, Christopher T. Walsh, The MerR Metalloregulatory Protein Binds Mercuric Ion as a Tricoordinate, Metal-Bridged Dimer[J], Science, 1998, 247, 946-948.<br>
+
5 Uri Alon (2007). An Introduction to Systems Biology—Design Principles of Biological Circuits[M], Chapman&Hall/CRC.
-
4 Diana. M, Ralston and Thomas V. O Halloran, Ultrasensitivity and heavy-metal selectivity of the allosterically modulated MerR transcription complex[J], PNAS, 1990, 87, 3846-3850.<br>
+
<br>
-
5 Uri Alon, An Introduction to Systems Biology—Design Principles of Biological Circuits[J], Chapman&Hall/CRC,2007.
+
6 Wickner, S., Maurizi, M. R. & Gottesman, S.(1999). Posttranslational Quality Control: Folding, Refolding, and Degrading Proteins. Science 286, 1888–1893.<br>
 +
7 W. Ma, A. Trusina, H. El-Samad, W.A. Lim, C. Tang (2009). Defining network topologies that can achieve biochemical adaptation. Cell 138, 760–773.<br>
 +
<br>
 +
<br>
 +
<b>Download the model part materials</b>
 +
<html>
 +
<br>
 +
<a href="https://static.igem.org/mediawiki/2010/7/73/PKU_Model_Part_One.pdf"><font color=000000><img src="https://static.igem.org/mediawiki/2010/9/91/PKU_Adobe_Reader_Logo.jpg" width=20><b><i>PART ONE</i></b></font></a>
 +
<br>
 +
<a href="https://static.igem.org/mediawiki/2010/b/bc/Wiki_semilog.pdf"><font color=000000><img src="https://static.igem.org/mediawiki/2010/9/91/PKU_Adobe_Reader_Logo.jpg" width=20><b><i>PART TWO</i></b></font></a>
 +
<br>
<br>
<br>
-
6 W. Ma, A. Trusina, H. El-Samad, W.A. Lim, C. Tang. Defining network topologies that can achieve biochemical adaptation[J]. Cell. 2009, 138:760–773.<br>
 
-
</font></font></font>
+
Any problem, please contact with <b>Zhenzhen Yin</b><i> evamail.pku AT gmail.com </i>Or <b>Yuheng Lu</b> <i>lgdeer AT gmail.com</i>
 +
<b>For more clear pictures, please click on it.</b>
 +
</html>
 +
 
 +
 
 +
 
<html>
<html>
Line 82: Line 100:
<a href="#top"><img src="https://static.igem.org/mediawiki/2010/8/87/Top.png" width="100px" height="75px"alt="go back to top"></a>
<a href="#top"><img src="https://static.igem.org/mediawiki/2010/8/87/Top.png" width="100px" height="75px"alt="go back to top"></a>
</div>
</div>
 +
</html>

Latest revision as of 02:22, 28 October 2010

Better visual effects via FireFox ~~~




   Modeling Home

Introduction

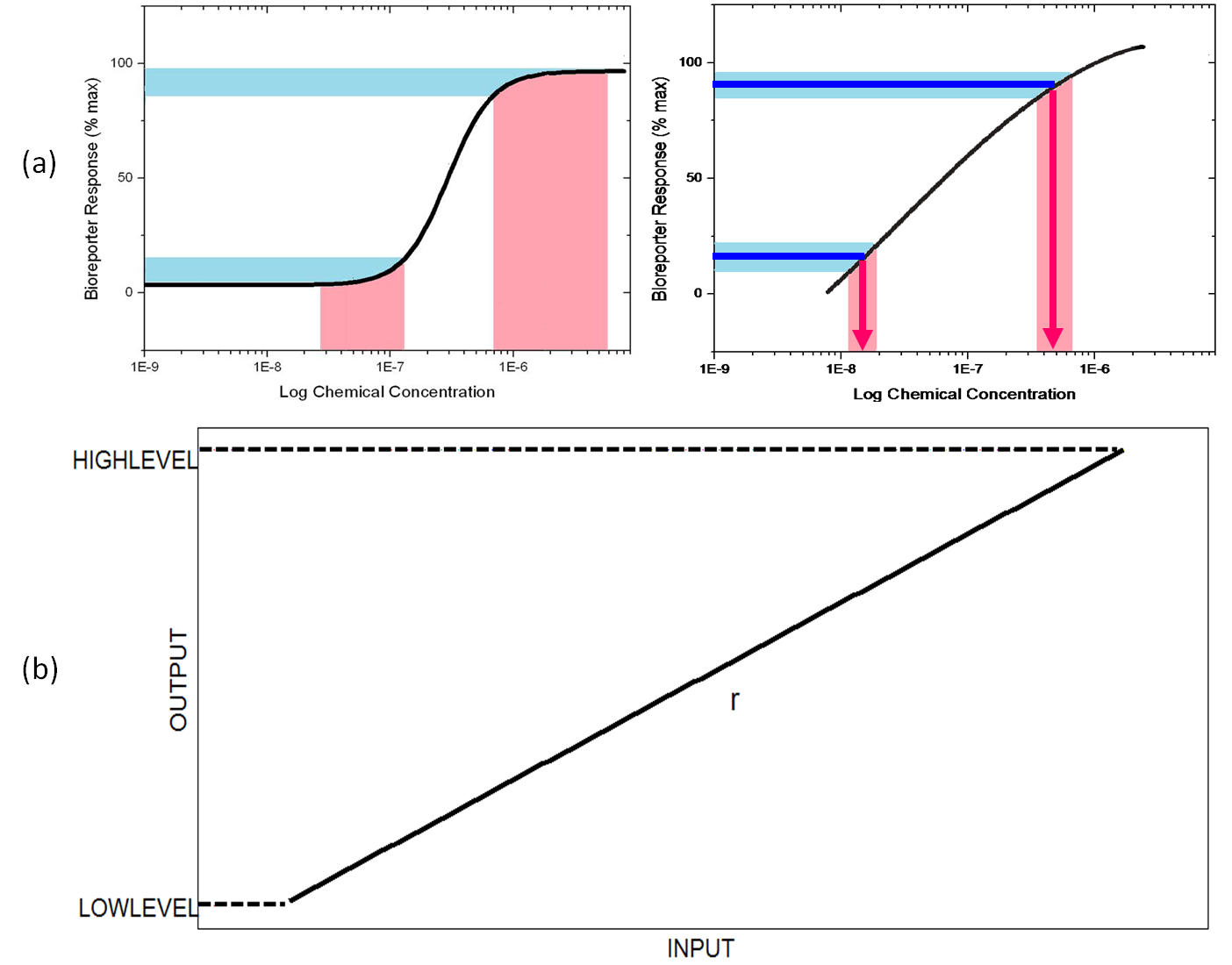
The biological systems are full of noises, and the response of bioreporters can be represented by a Hill Function. Noises will be significantly amplified and the output detected will be invalid at the ends of dose response curve.(Figure 1(a)) Therefore, The detection is limited at a narrow range. In order to solve the problem, we seek to transform the Hill Function curve to a straight line. As Figure 1(a) shows, the noise is reducted, and the sensitivity and detectable-range-characteristic of biosensors will be significantly improved.

Aimed at finding a genetic circuit that can perform the transformation, a simple and universal one for practice convenience, we adopted the process of Reverse engineering which in our work means to enumerate all possible networks and analyzed whether they function well, thus getting the right topology. In details, we first express the target functionalities in quantitative characters and set numerical standards according to our expectations, next define the network for simplest circuit search and derive equations precisely describing it, then calculate the characters using the equations and compare them with standards, then further analyze the comparison results and find the simplest functional network. Finally, to fully understand it and provide enough information for application, we analyze the mechanism and the parameter preferences, as well as exploring whether the very circuit is necessary for performing the function well.

Here we name our target functionality as Input-Output Alignment(IOA). In order to define IOA precisely for need of calculation, we considered most important characters of IOA and adopted Pearson Correlation Coefficient r to represent Input-Output Linear Relationship in the overall search work ( when r>0.99 we consider the network topology having the IOA function ), and also, regulated two levels for the initial and ultimate output concentration for the second character – the output range in further search work.(Figure 1(b))


Intro2.png



Figure 1 (a) The transformation reducts noises and make output more recognizable.(b)Factors for selection of IOA network topologies. r is the Pearson Correlation Coefficient and the output range is HIGHLEVEL minus LOWLEVEL.

Calculating Process

In this part, we will demostrate our calculating process in three sections--Network enumeration, Equations set up and network topologies’ analysis.
                                                                                                                                 == Learn more ==

Analyses and Results

Here we analyzed the results we obtained and found the final right topology.
                                                                                                                                 == Learn more ==

Advanced Model

When the range of input is very large, the IOA networks no longer meet out needs and so we tried to find one semilog-linear topology in this section.
                                                                                                                                 == Learn more ==

References

1 Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K. & Walter, P. (2008). Molecular Biology of the Cell (Garland, New York).
2 Nicolas E. Buchler, Ulrich Gerland, Terence Hwa (2005). Nonlinear protein degradation and the function of genetic circuits, PNAS 102, 9559-9564.
3 John D. Helmann, Barry T. Ballard, Christopher T. Walsh (1998). The MerR Metalloregulatory Protein Binds Mercuric Ion as a Tricoordinate, Metal-Bridged Dimer. Science 247, 946-948.
4 Diana. M, Ralston and Thomas V. O Halloran (1990). Ultrasensitivity and heavy-metal selectivity of the allosterically modulated MerR transcription complex. PNAS 87, 3846-3850.
5 Uri Alon (2007). An Introduction to Systems Biology—Design Principles of Biological Circuits[M], Chapman&Hall/CRC.
6 Wickner, S., Maurizi, M. R. & Gottesman, S.(1999). Posttranslational Quality Control: Folding, Refolding, and Degrading Proteins. Science 286, 1888–1893.
7 W. Ma, A. Trusina, H. El-Samad, W.A. Lim, C. Tang (2009). Defining network topologies that can achieve biochemical adaptation. Cell 138, 760–773.


Download the model part materials
PART ONE
PART TWO

Any problem, please contact with Zhenzhen Yin evamail.pku AT gmail.com Or Yuheng Lu lgdeer AT gmail.com For more clear pictures, please click on it.



go back to top

Retrieved from "http://2010.igem.org/Team:Peking/Modeling"