Team:USTC Software/Simulation
From 2010.igem.org
(→Chain Sorting and Weighting Scheme) |
(→Introduction) |
||
| (18 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Team:USTC_Software/Header}} | {{Team:USTC_Software/Header}} | ||
| - | + | =Introduction= | |
| - | We design and develop a software tool, ''iGame'', which supports database written in ''MoDeL'' format, to perform task of automatic modeling. Actually, automatic modeling is a database-dependent network-searching-and-developing process from the initial conditions. Besides the database, users are required to provide initial environment condition, such as initial plasmids with biobrick parts. ''iGame'' will generate the network of the biological system in ''SBML'' standard. Please refer to [https://2010.igem.org/Team:USTC_Software/User_Interface user interface] to know more about input and output of ''iGame''. | + | <br/> |
| + | We design and develop a software tool, ''iGame'', which supports database written in ''MoDeL'' format, to perform task of automatic modeling. Actually, automatic modeling is a database-dependent network-searching-and-developing process from the initial conditions. Besides the database, users are required to provide initial environment condition, such as initial plasmids with biobrick parts. ''iGame'' will generate the network of the biological system in ''SBML'' standard. Please refer to [https://2010.igem.org/Team:USTC_Software/<font size="5">''User_Interface user interface''</font>] to know more about input and output of ''iGame''. | ||
<font size="+1">'''Algorithms for automatic modeling will be shown in the following sections'''</font>. An overview is as follow: | <font size="+1">'''Algorithms for automatic modeling will be shown in the following sections'''</font>. An overview is as follow: | ||
| Line 11: | Line 12: | ||
*Section <font color="red">''Generation of products based on reaction templates''</font> describes the ''mix-trim-split'' method to generate products. | *Section <font color="red">''Generation of products based on reaction templates''</font> describes the ''mix-trim-split'' method to generate products. | ||
---- | ---- | ||
| + | <br/> | ||
| - | + | =Algorithm flow chart= | |
{| | {| | ||
| Line 39: | Line 41: | ||
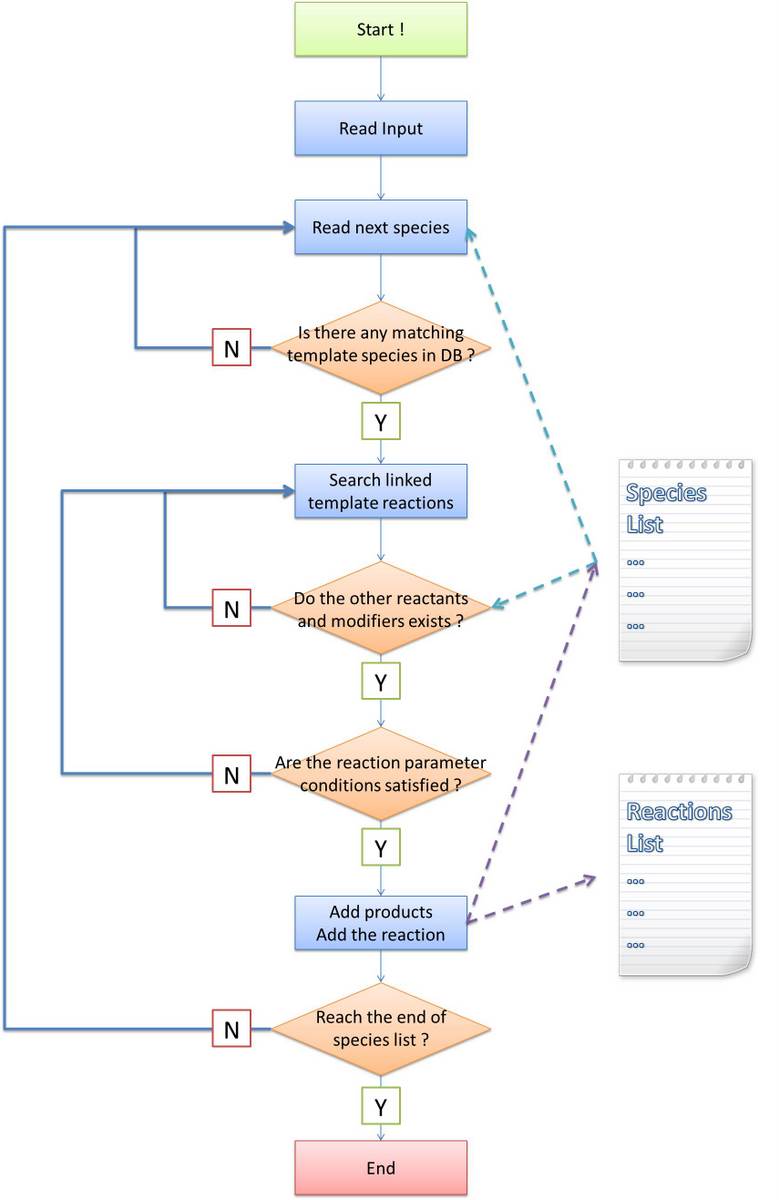
|[[Image:Ustcs Core workflow.jpg|thumb|300px|Figure 1: Algorithm Flow Chart]] | |[[Image:Ustcs Core workflow.jpg|thumb|300px|Figure 1: Algorithm Flow Chart]] | ||
| - | |||
|} | |} | ||
| - | + | ---- | |
| - | + | <br/> | |
| + | =Special reactions and volume strategy= | ||
| + | <br/> | ||
Transcription and translation reactions are not supported by ''MoDeL'' reaction definitions; they are handled specially in the core program. We use pseudo first-order reaction to model both transcription and translation reactions. The rate constant k is the value of ''forwardPromoterEfficiency''/''reversePromoterEfficiency'' for transcriptions and ''forwardRbsEfficiency''/''reverseRbsEfficiency'' for translations defined for each part in the database. It means number of mRNAs per DNA per second for transcriptions and number of proteins per mRNA per second for translations. A transcription will not end at a terminator with termination efficiency less than 100% (values are stored in attribute ''forwardTerminatorEfficiency''/''reverseTerminatorEfficiency''): RNA polymerase will pass over and continue transcription. For translation reactions, the prerequisite condition is that the part next to RBS along the 5' to 3' direction must have non-zero attribute value ''forwardStartCodon''/''reverseStartCodon''. Opposite to transcriptions, translation reactions would stop if one part with non-zero attribute value ''forwardStopCodon''/''reverseStopCodon'' is encountered. | Transcription and translation reactions are not supported by ''MoDeL'' reaction definitions; they are handled specially in the core program. We use pseudo first-order reaction to model both transcription and translation reactions. The rate constant k is the value of ''forwardPromoterEfficiency''/''reversePromoterEfficiency'' for transcriptions and ''forwardRbsEfficiency''/''reverseRbsEfficiency'' for translations defined for each part in the database. It means number of mRNAs per DNA per second for transcriptions and number of proteins per mRNA per second for translations. A transcription will not end at a terminator with termination efficiency less than 100% (values are stored in attribute ''forwardTerminatorEfficiency''/''reverseTerminatorEfficiency''): RNA polymerase will pass over and continue transcription. For translation reactions, the prerequisite condition is that the part next to RBS along the 5' to 3' direction must have non-zero attribute value ''forwardStartCodon''/''reverseStartCodon''. Opposite to transcriptions, translation reactions would stop if one part with non-zero attribute value ''forwardStopCodon''/''reverseStopCodon'' is encountered. | ||
| - | Volume strategy is a special method to solve problems introduced by diffusion reactions. Consider a transport reaction S1->S2 in which the species S1 is moved from the first compartment with volume V1, to the second with volume V2. The | + | Volume strategy is a special method to solve problems introduced by diffusion reactions. Consider a transport reaction S1->S2 in which the species S1 is moved from the first compartment with volume V1, to the second with volume V2. The rate constant is k but the rate law is not k*[S1]*V1, because the concentration conversion is needed. The correct expression is N*k*[S1]*V1. The volume strategy just uses N*V1 instead of V1 as the volume of the first compartment. To have a general definition, the volume of a compartment is defined as V*N1*N2, where: |
| - | + | *V is the volume of the compartment itself; | |
| - | + | *N1 is the number of compartments located in its outside compartment; | |
| + | *N2 is the total number of its outside compartment | ||
| + | ---- | ||
| + | <br/> | ||
| + | =Chain Sorting and Weighting Scheme= | ||
| + | <br/> | ||
Chains in our ''Chain-Node'' model should not have any order since there are no natural ways to sort them. One chain is not | Chains in our ''Chain-Node'' model should not have any order since there are no natural ways to sort them. One chain is not | ||
preferred to another, since in a complex of multiple chains, which are connected via binding interaction of binding bites on their own, all chains are equivalent. However, a chain-sorting program is a prerequisite for implementations of many other functions, such as comparison of two ''Chain-Node'' structures, or pattern matching of template species to those in the system. | preferred to another, since in a complex of multiple chains, which are connected via binding interaction of binding bites on their own, all chains are equivalent. However, a chain-sorting program is a prerequisite for implementations of many other functions, such as comparison of two ''Chain-Node'' structures, or pattern matching of template species to those in the system. | ||
| Line 55: | Line 63: | ||
If all chains are different in the first stage of sorting, we have already obtain the unique order of the chain list. However, it is not always so: equal chains in the above sorting may be equivalent or not. It is due to the assumption that two bound parts are taken as equal if both have same ''partReference''and ''partType'' attribute values. Though the above sorting strategy takes binding positions into consideration, it ignores the binding details of those parts: the details are hidden in the nodes of all trees. Hence, similar to the chain sorting, we need to find another strategy to sort nodes as well as trees. Our weighting scheme will be first introduced below. | If all chains are different in the first stage of sorting, we have already obtain the unique order of the chain list. However, it is not always so: equal chains in the above sorting may be equivalent or not. It is due to the assumption that two bound parts are taken as equal if both have same ''partReference''and ''partType'' attribute values. Though the above sorting strategy takes binding positions into consideration, it ignores the binding details of those parts: the details are hidden in the nodes of all trees. Hence, similar to the chain sorting, we need to find another strategy to sort nodes as well as trees. Our weighting scheme will be first introduced below. | ||
| - | Assume the chains are sorted already. Each part will be assigned a weight based on its position in the chain list. The weight of the jth part on the ith chain is (i,j). For example, the first part on the first chain posses a weight (0,0) (in ''C'' style, counting number from zero). After assignment of parts' weight, we turn to weights of the nodes in trees. Since leaf nodes in trees are actually the representation of parts in bound state on chains, the weight of each leaf node could be inherited from the weight of its corresponding part. For parent node, its weight equals to the maximum of weights of all its children nodes (we define a weight (i, j) is greater than another (i',j') if i < i' or i = i' while j < j'). The recursive definition of nodes' weight of trees makes it possible to sort all children | + | Assume the chains are sorted already. Each part will be assigned a weight based on its position in the chain list. The weight of the jth part on the ith chain is (i,j). For example, the first part on the first chain posses a weight (0,0) (in ''C'' style, counting number from zero). After assignment of parts' weight, we turn to weights of the nodes in trees. Since leaf nodes in trees are actually the representation of parts in bound state on chains, the weight of each leaf node could be inherited from the weight of its corresponding part. For parent node, its weight equals to the maximum of weights of all its children nodes (we define a weight (i, j) is greater than another (i',j') if i < i' or i = i' while j < j'). The recursive definition of nodes' weight of trees makes it possible to sort all children of each node, which is a prerequisite for generating Huffman codes (see below). And then the tree order in the forest could be uniquely determined by sorting the root node of each tree. |
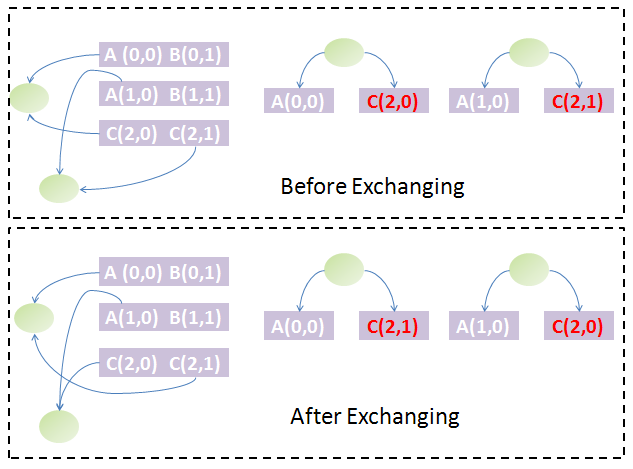
[[Image:USTCs_Chainsorting1.png|400px|thumb| Exchange of the first and second chain. The tree structures are different before and after exchange: the two chains are not equivalent.]] | [[Image:USTCs_Chainsorting1.png|400px|thumb| Exchange of the first and second chain. The tree structures are different before and after exchange: the two chains are not equivalent.]] | ||
Back to the question above, if two chains are equal in the first stage sorting, which should be arranged in front of the other? The answer could be obtained by exchanging them. The exchange will change the parts' weight on both chains and thus the weight of some nodes of the trees and subsequently the tree and forest structure. If the forest structure is not changed, the two chains are equivalent, which means that it makes no difference to arrange either chain in front of the other. If the forest structure has changed, we must find some ways to determine which tree structure is preferred and based on this to arrange them. We know each tree could be uniquely converted to a binary tree by taking the first child of each node as the left child and its siblings as its right child. The Huffman algorithm is used to generate the Huffman code of each node in the binary tree. Since the Huffman code of each node represents its path to the root node, we can restore the tree structure from the Huffman codes of all leaf nodes. Hence, the Huffman codes of leaf nodes could uniquely determine a tree structure. With help of Huffman codes, it is simple to compare the forest structure after and before exchange of both chains. | Back to the question above, if two chains are equal in the first stage sorting, which should be arranged in front of the other? The answer could be obtained by exchanging them. The exchange will change the parts' weight on both chains and thus the weight of some nodes of the trees and subsequently the tree and forest structure. If the forest structure is not changed, the two chains are equivalent, which means that it makes no difference to arrange either chain in front of the other. If the forest structure has changed, we must find some ways to determine which tree structure is preferred and based on this to arrange them. We know each tree could be uniquely converted to a binary tree by taking the first child of each node as the left child and its siblings as its right child. The Huffman algorithm is used to generate the Huffman code of each node in the binary tree. Since the Huffman code of each node represents its path to the root node, we can restore the tree structure from the Huffman codes of all leaf nodes. Hence, the Huffman codes of leaf nodes could uniquely determine a tree structure. With help of Huffman codes, it is simple to compare the forest structure after and before exchange of both chains. | ||
| - | To go further, we must define the preference of each forest structure due to exchange of chains: compare each node of the first tree by their Huffman codes and weights in the same way as strings and if equal, compare the next until difference appears or to the end of either forest. If one is less than another, it has higher priority. With this definition, the order of those equal chains in the first-stage sorting is determined by the one which generates the forest strucuture with highest priority among all possibilities. By performing this algorithm for all | + | To go further, we must define the preference of each forest structure due to exchange of chains: compare each node of the first tree by their Huffman codes and weights in the same way as comparison of strings and if equal, compare the next until difference appears or to the end of either forest. If one is less than another, it has higher priority. With this definition, the order of those equal chains in the first-stage sorting is determined by the one which generates the forest strucuture with highest priority among all possibilities. By performing this algorithm for all groups of equal chains obtained from the first-stage sorting, we could find both the unique order of the chains and the groups of equivalent chains (exchange of the order fo several chains in the same equivalent group will not change the forest structure). The figure illustrates this idea graphically. |
It is easy to compare two structures with help of chain sorting. We only need to compare first the chain list in order, chain by chain, and if equal, compare both associated forest structures. If two structures are same, the comparison must be equal since chains and trees are all in their unique order. If the comparison is equal, they must be the same structures since we could uniquely generate a Chain-Node structure from the chains as well as its associated forest structure. | It is easy to compare two structures with help of chain sorting. We only need to compare first the chain list in order, chain by chain, and if equal, compare both associated forest structures. If two structures are same, the comparison must be equal since chains and trees are all in their unique order. If the comparison is equal, they must be the same structures since we could uniquely generate a Chain-Node structure from the chains as well as its associated forest structure. | ||
| - | + | ---- | |
| - | + | <br/> | |
| - | < | + | =Structural pattern match of template species= |
| + | <br/> | ||
| + | '''We assume that if a combination of species in the species list could be structurally matched to reactants and modifiers templates defined within a reaction, they are possible to react with each other in the way as the reaction template describes'''. Hence, it is important to find such matchings between species in the species list and template ones defined in the database. We will first give the basic idea and then some modifications. | ||
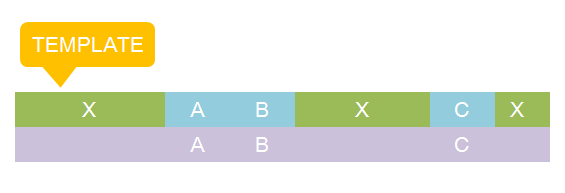
[[Image:USTCs_ChainMatching.png|400px|thumb| Blocks of ''ST'' and ''NST'' part on a template chain]] | [[Image:USTCs_ChainMatching.png|400px|thumb| Blocks of ''ST'' and ''NST'' part on a template chain]] | ||
[[Image:USTCs_ChainMatching2.png|400px|thumb| Combinations of ''NST'' block matchings form a region restriction for ''ST'' part blocks]] | [[Image:USTCs_ChainMatching2.png|400px|thumb| Combinations of ''NST'' block matchings form a region restriction for ''ST'' part blocks]] | ||
[[Image:USTCs_ChainMatching3.png|400px|thumb| The template ''ST'' block contains 3 ''ANY'' parts. If the first ''ANY'' part is matched A and B, the task is reduced to match the next 2 ''ANY'' parts to C, D, E, F, and G. All matchings could be found by recursively performing this algorithm.]] | [[Image:USTCs_ChainMatching3.png|400px|thumb| The template ''ST'' block contains 3 ''ANY'' parts. If the first ''ANY'' part is matched A and B, the task is reduced to match the next 2 ''ANY'' parts to C, D, E, F, and G. All matchings could be found by recursively performing this algorithm.]] | ||
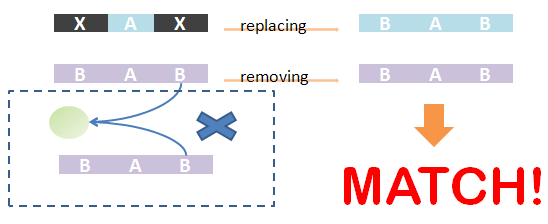
| - | [[Image: | + | [[Image:USTCs_chainMatching4.png|400px|thumb| Removing unmatched chains and associated trees of the species. It should have same structure with template species after replacing ''ST'' part with matchings if it has the same structural pattern with the template one.]] |
| - | The basic idea is simple. We first consider the structural pattern matching between one chain and a chain template. There are two kind of parts on a chain template: ''substituent''-type part (''ST'') and non-''substituent''-type part (''NST''). The whole template chain could be separated into blocks of ''ST'' parts and ''NST'' parts. Then we could break down the task to the matching of each small block. For each ''NST'' type block, we find all its matching regions on the chain to be matched | + | The basic idea is simple. We first consider the structural pattern matching between one chain and a chain template. There are two kind of parts on a chain template: ''substituent''-type part (''ST'') and non-''substituent''-type part (''NST''). The whole template chain could be separated into blocks of ''ST'' parts and ''NST'' parts. Then we could break down the task to the matching of each small block. For each ''NST'' type block, we find all its matching regions on the chain to be matched and there may be more than one regions. Each of the combinations of all ''NST'' blocks forms a ''NST'' frame and restricts the matching regions of ''ST'' blocks. Therefore, the task is reduced to find matchings of each ''ST'' part block within a restricted region on the chain to be matched. At the present version of ''MoDeL'', there are 6 ''ST'' part: ''ANY'', ''ANYUB'', ''NZ'', ''NZUB'', ''ONE'' and ''ONEUB''. A general algorithm for all 6 type part is designed and we will illustrate this via an example. Consider a ''ST'' block with all ''ANY'' type parts (we use ''X'' to indicate ''ANY'' type part in the figures). We find matchings of the first part of the block. There may be many possible matchings because part of type ''ANY'' implies arbitrary matching of parts on one chain in ''MoDeL'' definitions. For each matching found, we deal with the next, and do the same thing recursively until the end of the template or matching fails. An easy example is shown in the figure to illustrate this simple idea. |
| - | After all possible matchings for each chain in the template have been found, we could choose any one from each to form a combination. | + | After all possible matchings for each chain in the template have been found, we could choose any one from each to form a combination. In each combination, matchings of different chains should not be the same. For example, there are two chains in the template, T1 and T2, and three chains, C1, C2 and C3 in the species. If T1 has one matching to C1 and one to C2 and T2 has one to C2 and one to C3, the possible matchings are (T1,T2)->(C1, C2), (T1,T2)->(C1,C3) and (T1,T2)->(T2,T3). (T1,T2)->(C2,C2) is not allowed. The general matching relations could be written as (n1,n2,n3...)->(m1,m2,m3...), where (n1,n2,n3...) represents chains in the template and (m1,m2,m3...) represents the chains matched in the species for (n1,n2,n3...) respectively. However, it is only part of the matching relation because details, such as the matching positions of parts in the template, are ignored. The next question is: how to validate each matching? |
| - | As defined in | + | As defined in ''Chain-Node'' model, details of distribution of binding are stored in the forest. Matching of chains could not solely determine the overall match -- whether the template and the species have the same structural pattern. However, it is not easy to compare tree structure directly. We designed an algorithm to do this based on the principle: '''If the template and species have the same structural pattern, it must be possible to isolate the template from the species after replacing the ''ST'' part with its matchings'''. We first replace the ''ST'' part of the template with its matchings in the species. And then, we remove the chains which are not matched and the associated trees -- containing leaf nodes whose corresponding parts are on those chains. If the species after removing has the same ''Chain-Node'' structure with the template after replacing, the template and the species have the same structural pattern and in brief, the template could be matched to the species. We also illustrate this idea in figures. |
| - | However, there is one problem of this algorithm. Consider a LacI dimer template, whose | + | However, there is one problem of this algorithm. Consider a LacI dimer template, whose ''Chain-Node'' model has two chains with one part on each and one tree with 2 leaf nodes. And there is also a LacI dimer species, it has the same structural pattern with the template. The matching should be (T1,T2)->(C1,C2) and (T1,T2)->(C2,C1) according to the algorithm described above. However, there is indeed one matching since the two matchings are the same. The underlying reason is that the two chains of the template are equivalent: it makes no difference to the tree structure (Huffman code of each node) if they are exchanged. Hence, several equivalent chains should be matched to a certain set of chains in the species only once. |
| - | + | ||
| - | = | + | The algorithm of species matching is of the most importance since it provides technical support for structure-based description of species and reactions. It costs most of the running time. We will try to increase the efficiency of the codes of this part. |
| - | + | ||
| + | <br style="clear:both;"> | ||
| + | ---- | ||
| + | <br/> | ||
| + | =Generation of products based on reaction templates= | ||
| + | <br/> | ||
| + | Within ''MoDeL'' definitions, product templates are composed of both ''ST'' parts and ''NST'' parts. The ''ST'' parts are all transfered from reactants or modifiers. A transfer table is defined in each reaction template to label where does each ''ST'' part comes from and goes to. It seems to be very easy to generate ''Chain-Node'' structure of products from reactants and mod modifiers based on the transfer table. However, it doesn't. | ||
| - | Consider first a template reaction with one reactant, A-B, where A and B are both ''NST'' parts. If it could be digested by a certain enzyme, the products should be A and B. In the real biological system, if there is a species with structure C-A-B-C, where the first part C and the last C binds to form a tree node. If we try to digest the A-B bond, the species would not be split into two pieces as expected because the two products | + | Consider first a template reaction with one reactant, X-A-B-Y, where A and B are both ''NST'' parts and X and Y are both ''ST'' parts with type ''ANY''. If it could be digested by a certain enzyme, the products should be X-A and B-Y. In the real biological system, if there is a species with structure C-A-B-C, where the first part C and the last C binds to form a tree node. If we try to digest the A-B bond, the species would not be split into two pieces as expected because the two products are connected by the tree node. To generate the structure of products correctly, we design a three-step ''mix-trim-split'' algorithm to solve this problem. |
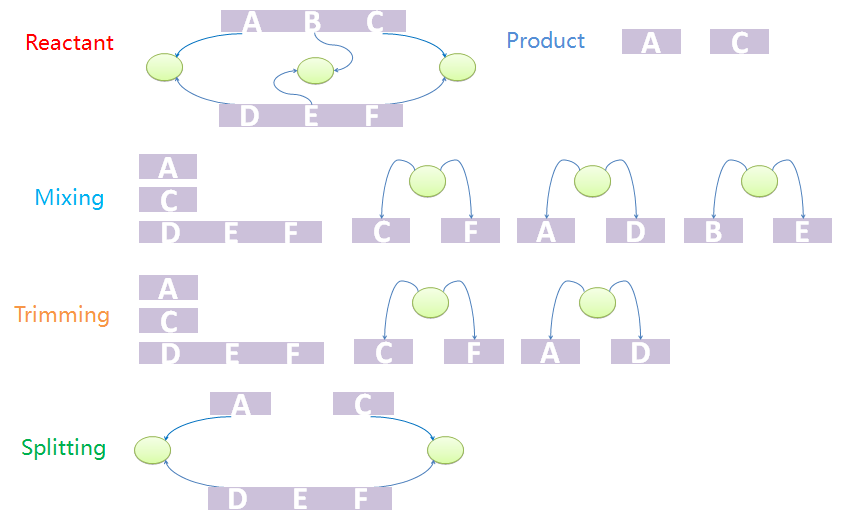
| - | [[Image:USTCs_Product.png|400px|thumb| Mixing, | + | [[Image:USTCs_Product.png|400px|thumb| Mixing, trimming and splitting: three-step algorithm to generate products.]] |
| - | The first step is to | + | The first step is to ''mix'' reactants and products. The mixture includes all chains of reactants except for those which are matched to the templates as well as all trees. It also includes all chains and trees of products. And now we have a mixed species with chains and trees from different sources. It is worth noting that chains and trees of modifiers will not be added into the mixture. The next step is to ''trim'' the trees. Trees with leaf nodes that are not defined in chains will be removed from the forest. The last step is to ''split'' the products out from the mixture. This is because the mixture may not be one standalone complex. For example, it may have two unbound and uncorrelated chains. In other words, some chains that are not connected with others via tree nodes should not be incorporated into other species. The final standalone split species are real products in the system. |
| - | We provide an example to illustrate the product-generating procedure. The reactant has two chains, A-B-C and D-E-F. A, B, C bind with D, E, F, respectively. The products are A and C. First we | + | We provide an example to illustrate the product-generating procedure. The reactant has two chains, A-B-C and D-E-F. A, B, C bind with D, E, F, respectively. The products are A and C. First we ''mix'' chains and trees. Chain A-B-C will not appear in the mixture. Since node B does not appear in mixed chains, tree with nodes B and E will be removed in the ''trim'' process. Because part C and F, A and D, are both bound to nodes, the final product should contain A and B both after ''split'' processing. |
| - | In the example above, there is only one product finally though two product templates are defined in database. | + | In the example above, there is only one product finally though two product templates are defined in database. What compartment does the product locate in if the two product templates locate in different compartments? A reasonable solution is to halve the quantities of the product and add it into both compartments. Another problem is that the corresponding reverse reaction would never be found because it fails to match two templates to only one species. The source of the two problems is essentially the same: how to describe intra-molecular reactions in framework of ''MoDeL'' language definitions. At present, it is not supported. However, supporting intra-molecular reactions is one of our future plans to refine our ''MoDeL'' language. |
Latest revision as of 18:29, 27 October 2010
Contents |
Introduction
We design and develop a software tool, iGame, which supports database written in MoDeL format, to perform task of automatic modeling. Actually, automatic modeling is a database-dependent network-searching-and-developing process from the initial conditions. Besides the database, users are required to provide initial environment condition, such as initial plasmids with biobrick parts. iGame will generate the network of the biological system in SBML standard. Please refer to User_Interface user interface to know more about input and output of iGame.
Algorithms for automatic modeling will be shown in the following sections. An overview is as follow:
- Section Algorithm flow chart gives an overall description of the general framework of our algorithms;
- Section Special reactions and volume strategy tells details about the methods and strategies our program utilizes to handle with some special reactions;
- Section Chain Sorting and Weighting Scheme provides details of sorting as well as weighting scheme and their functions;
- Section Structural pattern match of template species provides details of the core algorithm of iGame: how to find matchings between template species defined in database and species existed in the bio-system;
- Section Generation of products based on reaction templates describes the mix-trim-split method to generate products.
Algorithm flow chart
Before stating our own algorithm, we will first make an analysis about the difference and difficulty brought by introducing a new language system. The general algorithm idea is common: find out all species and reactions between them. Ignoring the efficiency of program, the most obvious method is doing the following recursively until no more species is generated:
Similar idea applies to our program. Some modifications must be made because in other software tools, reaction-searching is name-based. However, in our program, it is structure-based. Matching of species name is much easier than that of Chain-Node structure, which is featured as the most important part of our program. In addition, process of products generating is not as easy as just creating a new species with specific name, too. Their structures are required to be constructed under rules defined in MoDeL at the same time. The species matching and products generating modules are essential to implement our automatic modeling idea. To complete the final systemn network from initial conditions, we break up the task to several parts:
In the following, we will focus on the step (2), (3) and (5). Our algorithms are totally different with that of other software tools since we design them for the purpose of proving the feasibility of MoDeL for synthetic biology. They are kind of complicated because the complexity of biological systems require so. |
Special reactions and volume strategy
Transcription and translation reactions are not supported by MoDeL reaction definitions; they are handled specially in the core program. We use pseudo first-order reaction to model both transcription and translation reactions. The rate constant k is the value of forwardPromoterEfficiency/reversePromoterEfficiency for transcriptions and forwardRbsEfficiency/reverseRbsEfficiency for translations defined for each part in the database. It means number of mRNAs per DNA per second for transcriptions and number of proteins per mRNA per second for translations. A transcription will not end at a terminator with termination efficiency less than 100% (values are stored in attribute forwardTerminatorEfficiency/reverseTerminatorEfficiency): RNA polymerase will pass over and continue transcription. For translation reactions, the prerequisite condition is that the part next to RBS along the 5' to 3' direction must have non-zero attribute value forwardStartCodon/reverseStartCodon. Opposite to transcriptions, translation reactions would stop if one part with non-zero attribute value forwardStopCodon/reverseStopCodon is encountered.
Volume strategy is a special method to solve problems introduced by diffusion reactions. Consider a transport reaction S1->S2 in which the species S1 is moved from the first compartment with volume V1, to the second with volume V2. The rate constant is k but the rate law is not k*[S1]*V1, because the concentration conversion is needed. The correct expression is N*k*[S1]*V1. The volume strategy just uses N*V1 instead of V1 as the volume of the first compartment. To have a general definition, the volume of a compartment is defined as V*N1*N2, where:
- V is the volume of the compartment itself;
- N1 is the number of compartments located in its outside compartment;
- N2 is the total number of its outside compartment
Chain Sorting and Weighting Scheme
Chains in our Chain-Node model should not have any order since there are no natural ways to sort them. One chain is not
preferred to another, since in a complex of multiple chains, which are connected via binding interaction of binding bites on their own, all chains are equivalent. However, a chain-sorting program is a prerequisite for implementations of many other functions, such as comparison of two Chain-Node structures, or pattern matching of template species to those in the system.
Sorting is always performed under some rules. Since there are no natural options, we design one to generate the unique order for a list of chains. The rule we developed is something like that for comparing two strings: compare the first part of two chains by their partReference and partType in alphabet order and if equal, then compare the next until there are differences or to the end of either chain. At this stage, besides partReference and partType, two parts are considered equal if both are in bound states or not. There are some exceptions for DNA molecule: since dsDNA has both forward and reverse directions, comparison between its forward and reverse chain is also needed.
If all chains are different in the first stage of sorting, we have already obtain the unique order of the chain list. However, it is not always so: equal chains in the above sorting may be equivalent or not. It is due to the assumption that two bound parts are taken as equal if both have same partReferenceand partType attribute values. Though the above sorting strategy takes binding positions into consideration, it ignores the binding details of those parts: the details are hidden in the nodes of all trees. Hence, similar to the chain sorting, we need to find another strategy to sort nodes as well as trees. Our weighting scheme will be first introduced below.
Assume the chains are sorted already. Each part will be assigned a weight based on its position in the chain list. The weight of the jth part on the ith chain is (i,j). For example, the first part on the first chain posses a weight (0,0) (in C style, counting number from zero). After assignment of parts' weight, we turn to weights of the nodes in trees. Since leaf nodes in trees are actually the representation of parts in bound state on chains, the weight of each leaf node could be inherited from the weight of its corresponding part. For parent node, its weight equals to the maximum of weights of all its children nodes (we define a weight (i, j) is greater than another (i',j') if i < i' or i = i' while j < j'). The recursive definition of nodes' weight of trees makes it possible to sort all children of each node, which is a prerequisite for generating Huffman codes (see below). And then the tree order in the forest could be uniquely determined by sorting the root node of each tree.
Back to the question above, if two chains are equal in the first stage sorting, which should be arranged in front of the other? The answer could be obtained by exchanging them. The exchange will change the parts' weight on both chains and thus the weight of some nodes of the trees and subsequently the tree and forest structure. If the forest structure is not changed, the two chains are equivalent, which means that it makes no difference to arrange either chain in front of the other. If the forest structure has changed, we must find some ways to determine which tree structure is preferred and based on this to arrange them. We know each tree could be uniquely converted to a binary tree by taking the first child of each node as the left child and its siblings as its right child. The Huffman algorithm is used to generate the Huffman code of each node in the binary tree. Since the Huffman code of each node represents its path to the root node, we can restore the tree structure from the Huffman codes of all leaf nodes. Hence, the Huffman codes of leaf nodes could uniquely determine a tree structure. With help of Huffman codes, it is simple to compare the forest structure after and before exchange of both chains.
To go further, we must define the preference of each forest structure due to exchange of chains: compare each node of the first tree by their Huffman codes and weights in the same way as comparison of strings and if equal, compare the next until difference appears or to the end of either forest. If one is less than another, it has higher priority. With this definition, the order of those equal chains in the first-stage sorting is determined by the one which generates the forest strucuture with highest priority among all possibilities. By performing this algorithm for all groups of equal chains obtained from the first-stage sorting, we could find both the unique order of the chains and the groups of equivalent chains (exchange of the order fo several chains in the same equivalent group will not change the forest structure). The figure illustrates this idea graphically.
It is easy to compare two structures with help of chain sorting. We only need to compare first the chain list in order, chain by chain, and if equal, compare both associated forest structures. If two structures are same, the comparison must be equal since chains and trees are all in their unique order. If the comparison is equal, they must be the same structures since we could uniquely generate a Chain-Node structure from the chains as well as its associated forest structure.
Structural pattern match of template species
We assume that if a combination of species in the species list could be structurally matched to reactants and modifiers templates defined within a reaction, they are possible to react with each other in the way as the reaction template describes. Hence, it is important to find such matchings between species in the species list and template ones defined in the database. We will first give the basic idea and then some modifications.
The basic idea is simple. We first consider the structural pattern matching between one chain and a chain template. There are two kind of parts on a chain template: substituent-type part (ST) and non-substituent-type part (NST). The whole template chain could be separated into blocks of ST parts and NST parts. Then we could break down the task to the matching of each small block. For each NST type block, we find all its matching regions on the chain to be matched and there may be more than one regions. Each of the combinations of all NST blocks forms a NST frame and restricts the matching regions of ST blocks. Therefore, the task is reduced to find matchings of each ST part block within a restricted region on the chain to be matched. At the present version of MoDeL, there are 6 ST part: ANY, ANYUB, NZ, NZUB, ONE and ONEUB. A general algorithm for all 6 type part is designed and we will illustrate this via an example. Consider a ST block with all ANY type parts (we use X to indicate ANY type part in the figures). We find matchings of the first part of the block. There may be many possible matchings because part of type ANY implies arbitrary matching of parts on one chain in MoDeL definitions. For each matching found, we deal with the next, and do the same thing recursively until the end of the template or matching fails. An easy example is shown in the figure to illustrate this simple idea.
After all possible matchings for each chain in the template have been found, we could choose any one from each to form a combination. In each combination, matchings of different chains should not be the same. For example, there are two chains in the template, T1 and T2, and three chains, C1, C2 and C3 in the species. If T1 has one matching to C1 and one to C2 and T2 has one to C2 and one to C3, the possible matchings are (T1,T2)->(C1, C2), (T1,T2)->(C1,C3) and (T1,T2)->(T2,T3). (T1,T2)->(C2,C2) is not allowed. The general matching relations could be written as (n1,n2,n3...)->(m1,m2,m3...), where (n1,n2,n3...) represents chains in the template and (m1,m2,m3...) represents the chains matched in the species for (n1,n2,n3...) respectively. However, it is only part of the matching relation because details, such as the matching positions of parts in the template, are ignored. The next question is: how to validate each matching?
As defined in Chain-Node model, details of distribution of binding are stored in the forest. Matching of chains could not solely determine the overall match -- whether the template and the species have the same structural pattern. However, it is not easy to compare tree structure directly. We designed an algorithm to do this based on the principle: If the template and species have the same structural pattern, it must be possible to isolate the template from the species after replacing the ST part with its matchings. We first replace the ST part of the template with its matchings in the species. And then, we remove the chains which are not matched and the associated trees -- containing leaf nodes whose corresponding parts are on those chains. If the species after removing has the same Chain-Node structure with the template after replacing, the template and the species have the same structural pattern and in brief, the template could be matched to the species. We also illustrate this idea in figures.
However, there is one problem of this algorithm. Consider a LacI dimer template, whose Chain-Node model has two chains with one part on each and one tree with 2 leaf nodes. And there is also a LacI dimer species, it has the same structural pattern with the template. The matching should be (T1,T2)->(C1,C2) and (T1,T2)->(C2,C1) according to the algorithm described above. However, there is indeed one matching since the two matchings are the same. The underlying reason is that the two chains of the template are equivalent: it makes no difference to the tree structure (Huffman code of each node) if they are exchanged. Hence, several equivalent chains should be matched to a certain set of chains in the species only once.
The algorithm of species matching is of the most importance since it provides technical support for structure-based description of species and reactions. It costs most of the running time. We will try to increase the efficiency of the codes of this part.
Generation of products based on reaction templates
Within MoDeL definitions, product templates are composed of both ST parts and NST parts. The ST parts are all transfered from reactants or modifiers. A transfer table is defined in each reaction template to label where does each ST part comes from and goes to. It seems to be very easy to generate Chain-Node structure of products from reactants and mod modifiers based on the transfer table. However, it doesn't.
Consider first a template reaction with one reactant, X-A-B-Y, where A and B are both NST parts and X and Y are both ST parts with type ANY. If it could be digested by a certain enzyme, the products should be X-A and B-Y. In the real biological system, if there is a species with structure C-A-B-C, where the first part C and the last C binds to form a tree node. If we try to digest the A-B bond, the species would not be split into two pieces as expected because the two products are connected by the tree node. To generate the structure of products correctly, we design a three-step mix-trim-split algorithm to solve this problem.
The first step is to mix reactants and products. The mixture includes all chains of reactants except for those which are matched to the templates as well as all trees. It also includes all chains and trees of products. And now we have a mixed species with chains and trees from different sources. It is worth noting that chains and trees of modifiers will not be added into the mixture. The next step is to trim the trees. Trees with leaf nodes that are not defined in chains will be removed from the forest. The last step is to split the products out from the mixture. This is because the mixture may not be one standalone complex. For example, it may have two unbound and uncorrelated chains. In other words, some chains that are not connected with others via tree nodes should not be incorporated into other species. The final standalone split species are real products in the system.
We provide an example to illustrate the product-generating procedure. The reactant has two chains, A-B-C and D-E-F. A, B, C bind with D, E, F, respectively. The products are A and C. First we mix chains and trees. Chain A-B-C will not appear in the mixture. Since node B does not appear in mixed chains, tree with nodes B and E will be removed in the trim process. Because part C and F, A and D, are both bound to nodes, the final product should contain A and B both after split processing.
In the example above, there is only one product finally though two product templates are defined in database. What compartment does the product locate in if the two product templates locate in different compartments? A reasonable solution is to halve the quantities of the product and add it into both compartments. Another problem is that the corresponding reverse reaction would never be found because it fails to match two templates to only one species. The source of the two problems is essentially the same: how to describe intra-molecular reactions in framework of MoDeL language definitions. At present, it is not supported. However, supporting intra-molecular reactions is one of our future plans to refine our MoDeL language.
 "
"