Team:Imperial College London/Modelling/Protein Display/Detailed Description

From 2010.igem.org

(Difference between revisions)
m
m (Proof read)
Line 60: Line 60:
It was necessary to calculate the volume of the cell wall as we needed it for the calculation of concentrations in the enzymatic reaction.<br/>
It was necessary to calculate the volume of the cell wall as we needed it for the calculation of concentrations in the enzymatic reaction.<br/>
-
Volume of ''B. subtilis'' is 2.79μm<sup>3</sup> and the thickness of the cell wall is 35nm <a href="http://jb.asm.org/cgi/reprint/176/5/1413?ijkey=27dafbac7e23dee50390d3fe67d9d1bab0c6f48c">[5]</a>. In order to approximate the cell wall volume, assume that ''B. subtilis'' is a sphere - not a rod. Calculate the outer radius from the total volume: 0.874μm. Now subtract the thickness of the cell wall from the outer radius to determine the inner radius of the sphere: 0.839μm. The volume of the cell wall is equal to the difference between outer volume and the inner volume (calculated from the inner radius): <b>cell wall volume=0.32&times;10<sup>-15</sup>m<sup>3</sup></b>
+
Volume of <i>B. subtilis</i> is 2.79μm<sup>3</sup> and the thickness of the cell wall is 35nm <a href="http://jb.asm.org/cgi/reprint/176/5/1413?ijkey=27dafbac7e23dee50390d3fe67d9d1bab0c6f48c">[5]</a>. In order to approximate the cell wall volume, assume that <i>B. subtilis</i> is a sphere - not a rod. Calculate the outer radius from the total volume: 0.874μm. Now subtract the thickness of the cell wall from the outer radius to determine the inner radius of the sphere: 0.839μm. The volume of the cell wall is equal to the difference between outer volume and the inner volume (calculated from the inner radius): <b>cell wall volume=0.32&times;10<sup>-15</sup>m<sup>3</sup></b>
<h2>5. Control volume selection</h2>
<h2>5. Control volume selection</h2>
-
Note that the product of the enzymatic reaction, AIP, is allowed to diffuse outside the cell. Hence, it is important to take into account the cell boundaries. It is worth considering whether diffusion or fluid movements will play a significant role.
+
Note that the product of the enzymatic reaction, AIP, is allowed to diffuse outside the cell. Hence, it is important to determine the boundaries of the system. It is worth considering whether diffusion or fluid movements will play a significant role.
<br/>
<br/>
-
<p>Initially, we defined a control volume assuming that bacteria would grow in close colonies on the plate. We realized that our initial choice of control volume was not accurate, since our bacteria are meant to be used in suspension so we had to reconsider this issue.
+
<p>Initially, we defined a control volume assuming that bacteria would grow in close colonies on the plate. We realized that our initial choice of control volume was not accurate, since our bacteria are meant to be used in suspension so we had to reconsider this issue. If you wish to have a look at our initial working, click on the button below.
<br/></p>
<br/></p>
-
This control volume is considered to be wrong, but the details were kept for reference.<br/>
 
-
<br />
 
<div id="wrapper">
<div id="wrapper">
  <div class="accordionButton">Initial Choice of Control Volume</div>
  <div class="accordionButton">Initial Choice of Control Volume</div>
   <div class="accordionContent">
   <div class="accordionContent">
 +
This control volume is considered to be wrong, but the details were kept for reference.<br/>
<b>Control volume initial choice</b><br/>
<b>Control volume initial choice</b><br/>
Line 84: Line 83:
  |[[Image:IC_Outer_Volume.JPG|300px]]
  |[[Image:IC_Outer_Volume.JPG|300px]]
  |-
  |-
-
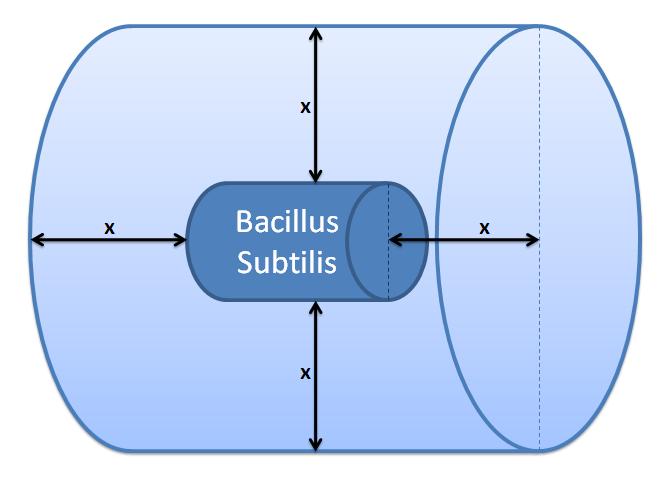
  |Control volume (Volume of B.sub to be excluded.<br/> x indicates the distance travelled by AIPs from<br/> the surface in time t).
+
  |Control volume (Volume of <i>B. subtilis</i> to be excluded.<br/> x indicates the distance travelled by AIPs from<br/> the surface in time t).
  |}
  |}
</div>
</div>
Line 128: Line 127:
<b>Choice of Control Volume allows simplifications</b><br/>
<b>Choice of Control Volume allows simplifications</b><br/>
<CENTER><img src="https://static.igem.org/mediawiki/2010/7/7c/Enz_react11.png"/> </CENTER>
<CENTER><img src="https://static.igem.org/mediawiki/2010/7/7c/Enz_react11.png"/> </CENTER>
-
Firstly, assume that the cells will be placed in the centre of the CV. Hence, after cleavage the protein will have an average distance of y/2 to travel in order to cross the boundary of the CV. This is calculated to happen within 0.2s. Even if the bacterium was not placed in the centre of the CV, the protein will travel from one end of the cube to the other in less than one second (~0.8s). Hence, it will take between 0.18 and 0.74s for the concentration of AIPs around the cell to be uniform. Noticing that these time values are not very small when molecular level is concerned, we decided that control volume is too big to give us a good approximation of what is happening.
+
Firstly, assume that the cells will be placed in the centre of the CV. Hence, after cleavage the protein will have an average distance of y/2 to travel in order to cross the boundary of the CV. This is calculated to happen within 0.2s. Even if the bacterium was not placed in the centre of the CV, the protein will travel from one end of the cube to the other in less than one second (~0.8s). Hence, it will take almost a second for the concentration of AIPs around the cell to be uniform. Noticing that this time value is not very small when molecular level is concerned, we decided that control volume is too big to give us a good approximation of what is happening.
<h2>6. Localised concentrations</h2>
<h2>6. Localised concentrations</h2>
Line 147: Line 146:
<li>c = 1.24&times;10<sup>-3</sup> mol/L. This is the concentration of protein that will be displayed on a single cell of B.sub.  
<li>c = 1.24&times;10<sup>-3</sup> mol/L. This is the concentration of protein that will be displayed on a single cell of B.sub.  
</ul>
</ul>
 +
 +
Hence, we can deduce that the final concentraion that the protein expression will tend to is: c = 1.24&times;10<sup>-3</sup> mol/dm<sup>3</sup> = c<sub>final</sub>. This value will be the initial concentration of protein that is cleaved by TEV. The simple production of protein by transcription and translation was incorporated into model using the following equation.
<br />
<br />
-
Hence, we can deduce that the final concentration that the protein expression will tend to is: c = 1.24&times;10<sup>-3</sup> mol/dm<sup>3</sup> = c<sub>final</sub>.
+
<CENTER><img src="https://static.igem.org/mediawiki/2010/d/d3/IC_Equation_3.png"/></CENTER>
-
<br /><br />
+
In the equation above: [p] = protein concentration, s = protein production rate, d = protein degradation rate<br/>
-
Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards c<sub>final</sub>. The degradation rate was kept constant (same as used in output amplification module), and the production rate was adjusted match the final concentration to be achieved.
+
<br />
<br />
-
Using a similar model to the simple production of Dioxygenase for the Output Amplification Model (<a href="https://2010.igem.org/Team:Imperial_College_London/Modelling/Output">Model preA</a>), we obtain the following graph:  
+
Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards c<sub>final</sub> according to the ODE below. The degradation rate was kept constant (same as used in output amplification module). This allowed us to generate the following data:
<br />
<br />
</html>
</html>

Revision as of 16:01, 27 October 2010

Modelling Overview | Detection Model | Signaling Model | Fast Response Model | Interactions
A major part of the project consisted of modelling each module. This enabled us to decide which ideas we should implement. Look at the Fast Response page for a great example of how modelling has made a major impact on our design!
Objectives | Description | Results | Constants | MATLAB Code
Detailed Description
This model consists of seven parts that had to be developed:
  1. Identification of all active and relevant elements of the isolated part of the system.
  2. Identification of interactions between the identified elements.
  3. Determining the threshold concentration of Auto Inducing Peptide (AIP) needed for activation of the receptor.
  4. Determining the volume of the cell wall.
  5. Defining a control volume around the bacterial cell (after cleavage, the surface protein will float around in the extracellular environment).
  6. Determining the importance of localised concentrations in a control volume.
  7. Determining the surface protein production to estimate the maximum abundance on the bacterial surface.

1. Elements of the system

  1. The surface protein consists of a cell wall binding domain, a linker and AIP (Auto Inducing Peptide). It is expressed by constitutive gene expression. It was assumed that the bacteria would be fully grown before carrying out the detection so the cell wall would be covered with as many surface proteins as the cell can maintain.
  2. Schistosoma elastase (enzyme released by the parasite) cleaves the AIP from the cell wall binding domain at the linker site. In the laboratory, we used TEV protease as we could not get hold of Schistosoma elastase, so the model was adjusted appropriately (TEV enzyme kinetic parameters were used).
  3. The ComD receptor is activated by a sufficiently high AIP concentration. Once activated, ComD signals into the cell to activate the colour response.

2. Interactions between elements

Apart from the proteins being expressed from genes, there was only one more chemical reaction identified in this part of the system. This is the cleavage of proteins, which is an enzymatic reaction:
    E+S <var>↔</var> ES <var>→</var>
  • Substrate (S) = Protein
  • Enzyme (E) = TEV (Protease)
  • Product (P) = Peptide

This enzymatic reaction can be rewritten as a set of ordinary differential equations (ODEs), which is of similar form to the 1-step amplification model.
This model is quite peculiar as we realised that its behaviour is not only dependent on time, but space as well. Namely, the cleavage reaction happens on the cell wall of the bacteria. However, AIP that has already been cleaved is allowed to diffuse in any direction. Since we were not sure how to model this scenario, we decided to determine the importance of localised concentrations in a control volume.

3. Threshold concentration of AIP

The optimal peptide concentration required to activate ComD is 10 ng/ml [1]. This is the threshold value for ComD activation. However, the minimum concentration of peptide to give a detectable activation is 0.5ng/ml.
The threshold for the minimal activation of the receptor is cth=4.4658×10-9 mol/L. Click on the button below to uncover the conversion from ng/ml to mol/L.
Converting 10 ng/ml to 4.4658×10-9 mol/L
  • The mass of a peptide is 2.24kDa = 3.7184×10-21g.
  • The number of molecules in one ml is 10ng/3.7184×10-21g = 2.6893×1012. In a litre, the number of molecules is 2.6893×1015molecules/L.
  • Dividing this value by Avogadro's constant gives the threshold concentration of cth=4.4658×10-9 mol/L.
  • The threshold for minimal activation of a receptor is 2.2329×10-10 mol/L.


4. Cell Wall Volume

It was necessary to calculate the volume of the cell wall as we needed it for the calculation of concentrations in the enzymatic reaction.
Volume of B. subtilis is 2.79μm3 and the thickness of the cell wall is 35nm [5]. In order to approximate the cell wall volume, assume that B. subtilis is a sphere - not a rod. Calculate the outer radius from the total volume: 0.874μm. Now subtract the thickness of the cell wall from the outer radius to determine the inner radius of the sphere: 0.839μm. The volume of the cell wall is equal to the difference between outer volume and the inner volume (calculated from the inner radius): cell wall volume=0.32×10-15m3

5. Control volume selection

Note that the product of the enzymatic reaction, AIP, is allowed to diffuse outside the cell. Hence, it is important to determine the boundaries of the system. It is worth considering whether diffusion or fluid movements will play a significant role.

Initially, we defined a control volume assuming that bacteria would grow in close colonies on the plate. We realized that our initial choice of control volume was not accurate, since our bacteria are meant to be used in suspension so we had to reconsider this issue. If you wish to have a look at our initial working, click on the button below.

Initial Choice of Control Volume
This control volume is considered to be wrong, but the details were kept for reference.
Control volume initial choice
The control volume: The inner boundary is determined by the bacterial cell (proteins after being displayed and cleaved cannot diffuse back into bacterium). The outer boundary is more time scale dependent. We have assumed that after mass cleavage of the display-proteins by TEV, many of these AIPs will bind to the receptors quite quickly (eg. 8 seconds). Our volume is determined by the distance that AIPs could travel outwards by diffusion within that short time. In this way, we are sure that the concentration of AIPs outside our control volume after a given time is approximately 0. This approach is not very accurate and can lead us to false negative conclusions (as in reality there will be a concentration gradient, with highest concentration on the cell wall).
IC Outer Volume.JPG
Control volume (Volume of B. subtilis to be excluded.
x indicates the distance travelled by AIPs from
the surface in time t).


Difussion distance was calculated using Fick's 1st Law: x=√2Dt, where: x - diffusion distance, D - diffusion constant, t - time of diffusion
Daverage = 10.7×10-11 m2s-1 for a protein in agarose gel for pH=5.6 [3]
t = 8s (arbitrarily chosen)
This gives: x = 4.14×10-5m
The control volume can be calculated by adding 2x to the length and the diamter of the cell.
This gives a control volume (CV) = 4.81×10-7m3




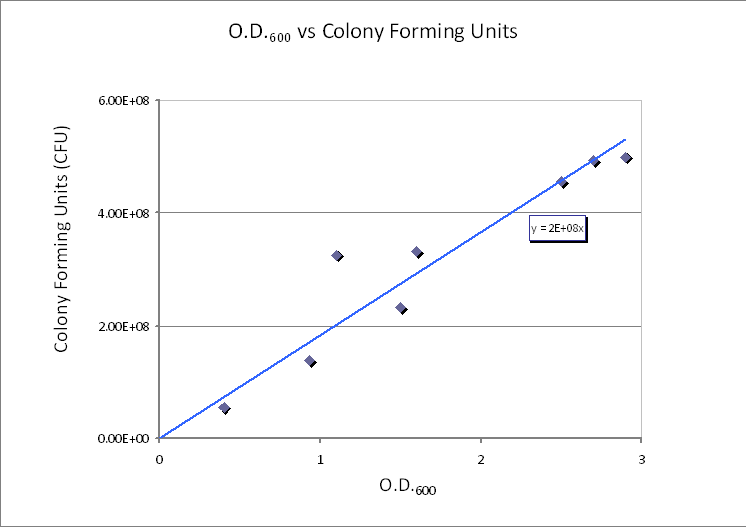
Using CFU to estimate the spacing between cells
CFU stands for Colony-forming unit. It is a measure of bacterial numbers. For liquids, CFU is measured per ml. We already have data of CFU/ml from the Imperial iGEM 2008 team, so we could use this data to estimate the number of cells in a given volume using a spectrometer at 600nm wavelength. The graph below is taken from the Imperial iGEM 2008 Wiki page [4].

IC Calibration-Dilution.PNG
CFU/ml vs. Optical Density at 600nm (OD600).


The graph shows values of CFU/ml for different optical densities. The range of CFU/ml is therefore between 0.5×108 - 5×108.
In this calculation, we assumed that only one cell will grow and become one colony (i.e. no more than one cell will form no more than one colony). Therefore, the maximum number of cells in 1ml of solution is 5×108. Taking the volume of 1 ml = 10-3 dm3 and dividing by the (maximum) number of cells in 1ml gives the average control volume (CV) around each cell: 2×10-12 dm3/cell. For simplicity, we choose the control volume to be cubic. Taking the third root of this value gives the length of each side of the control volume.

Side length of cubic Control volume is y = 1.26×10-4 dm = 1.26×10-5 m.

Choice of Control Volume allows simplifications
Firstly, assume that the cells will be placed in the centre of the CV. Hence, after cleavage the protein will have an average distance of y/2 to travel in order to cross the boundary of the CV. This is calculated to happen within 0.2s. Even if the bacterium was not placed in the centre of the CV, the protein will travel from one end of the cube to the other in less than one second (~0.8s). Hence, it will take almost a second for the concentration of AIPs around the cell to be uniform. Noticing that this time value is not very small when molecular level is concerned, we decided that control volume is too big to give us a good approximation of what is happening.

6. Localised concentrations

Since we failed to determine a control volume across which concentration of AIP could be assumed to be uniform, it was deduced that localised concentrations will play an important role in this model. Hence, we tried to come up with some kind of measure of localised concentrations. As the whole reaction happens at the wall and just the final product (AIP) floats freely around, we decided just to scale the AIP concentration by a factor after completion of reaction to simulate the loss of AIPs that diffuse away from cell surface.
It was arbitrarily chosen that 20% to 50% of AIPs will bind to receptors rather than diffuse away. There are several arguments that would suggest this kind of percentage:
  • AIPs being very close to the cell surface will have an equal probability of heading back towards the bacterium as diffusing away from it (since the cell is a lot bigger than the AIPs).
  • It is likely that there will be some chemical interactions between AIPs and the bacterium that could be attracting the AIPs to the host bacterium (e.g. electrostatic attraction could be possible).
The localised concentration coefficient scales the AIP concentrations at the very end - after the ODE equations have been solved.

7. Protein production

  • This paper mentions that each cell displays 2.4×105 peptides. [2]
  • 2.4×105 molecules = 2.4×105/6.02×1023 mol = 0.398671×10-18 mol
  • Volume of B.sub cell wall: 0.32×10-15m3
  • Concentration = [mol/L]
  • c = 1.24×10-3 mol/L. This is the concentration of protein that will be displayed on a single cell of B.sub.
Hence, we can deduce that the final concentraion that the protein expression will tend to is: c = 1.24×10-3 mol/dm3 = cfinal. This value will be the initial concentration of protein that is cleaved by TEV. The simple production of protein by transcription and translation was incorporated into model using the following equation.
In the equation above: [p] = protein concentration, s = protein production rate, d = protein degradation rate

Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards cfinal according to the ODE below. The degradation rate was kept constant (same as used in output amplification module). This allowed us to generate the following data:

IC Protein production.jpg
Production of protein by transcription and translation.


References

  1. Havarstein, L., Coomaraswamy, G. & Morrison, D. (1995) An unmodified heptadecapeptide pheromone induces competence for genetic transformation in Streptococcus pneumoniae. Proc. Natl. [Online] 92, 11140-11144. Available from: http://ukpmc.ac.uk/backend/ptpmcrender.cgi?accid=PMC40587&blobtype=pdf [Accessed 27th August 2010]
  2. Kobayashi, G. et al (2000) Accumulation of an artificial cell wall-binding lipase by Bacillus subtilis wprA and/or sigD mutants. FEMS Microbiology Letters. [Online] 188(2000), 165-169. Available from: http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09188.x/pdf [Accessed 27th August 2010]
  3. Gutenwik, J., Nilsson, B. & Axelsson, A. (2003) Determination of protein diffusion coefficients in agarose gel with a diffusion cell. Biochemical Engineering Journal. [Online] 19(2004), 1-7. Available from: http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6V5N-4B3MXDC-2-K&_cdi=5791&_user=217827&_pii=S1369703X03002377&_origin=search&_coverDate=07%2F01%2F2004&_sk=999809998&view=c&wchp=dGLzVtb-zSkzS&md5=c17d0e7320f03931006f9b1a10a438b9&ie=/sdarticle.pdf [Accessed August 20th 2010]
  4. Imperial College London (2008) Biofabricator Subtilis - Designer Genes. [Online] Available from: https://2008.igem.org/Imperial_College/18_September_2008 [Accessed 1st September 2010]
  5. Graham L. L. & Beverisge T. J. (1993) Structural Differentiation of the Bacillus subtilis 168 Cell Wall. Journal of Bacteriolofy. [Online] 5(1994), 1413-1420. Available from: http://jb.asm.org/cgi/reprint/176/5/1413?ijkey=27dafbac7e23dee50390d3fe67d9d1bab0c6f48c [Accessed October 26th 2010]

Retrieved from "http://2010.igem.org/Team:Imperial_College_London/Modelling/Protein_Display/Detailed_Description"