Team:Imperial College London/Modelling/Protein Display/Detailed Description
From 2010.igem.org
(Added the equations) |
(Rearranging) |
||
| Line 11: | Line 11: | ||
<li>Identification of all active and relevant elements of the isolated part of the system.</li> | <li>Identification of all active and relevant elements of the isolated part of the system.</li> | ||
<li>Identification of interactions between the identified elements.</li> | <li>Identification of interactions between the identified elements.</li> | ||
| - | <li>Identification of threshold concentration of auto inducing peptide (AIP) needed for activation of the receptor.</li> | + | <li>Identification of threshold concentration of auto inducing peptide (AIP) needed for activation of the receptor.</li> |
| + | <li>Determining the volume of cell wall.</li> | ||
<li>Defining a control volume around the bacterial cell (after cleavage, the surface protein will float around in the extracellular environment).</li> | <li>Defining a control volume around the bacterial cell (after cleavage, the surface protein will float around in the extracellular environment).</li> | ||
| + | <li>Determining the importance of localised concentrations in a Control Volume.</li> | ||
<li>Determining the surface protein production to estimate the maximum abundance on the bacterial surface.</li> | <li>Determining the surface protein production to estimate the maximum abundance on the bacterial surface.</li> | ||
</ol> | </ol> | ||
| Line 35: | Line 37: | ||
<CENTER><img src="https://static.igem.org/mediawiki/2010/9/9c/Enz_react10.png"/></CENTER> | <CENTER><img src="https://static.igem.org/mediawiki/2010/9/9c/Enz_react10.png"/></CENTER> | ||
| + | |||
| + | This model is quite peculiar as we realised that its behaviour is not only a function of time, but space as well. Namely, the cleavage reaction happens on the cell wall of bacteria. However, cleaved already AIP is allowed to diffuse is any direction. We were not sure how to model this scenario, so we decided to determine the importance of localised concentrations in a Control Volume. | ||
<h2>3. Threshold concentration of AIP</h2> | <h2>3. Threshold concentration of AIP</h2> | ||
| Line 53: | Line 57: | ||
</div> | </div> | ||
<br/><br/> | <br/><br/> | ||
| + | <h2>4. Cell Wall Volume</h2> | ||
| - | + | The volume of the cell wall was necessary to be calculated for calculation of concentrations in enzymatic reaction.<br/> | |
| - | + | Volume of B. subtilis is 2.79μm<sup>3</sup> and the thickness of cell wall is 35nm <a href="http://jb.asm.org/cgi/reprint/176/5/1413?ijkey=27dafbac7e23dee50390d3fe67d9d1bab0c6f48c">[5]</a>. In order to approximate the cell wall volume assume that B. subtilis is a sphere - not a rod. Calculate the outer radius from the total volume: 0.874μm. Now subtract the thickness of cell wall from outer radius to determine inner radius of the sphere: 0.839μm. The volume of cell wall equals to the difference between outer volume and the inner volume (calculated from inner radius): <b>cell wall volume=0.32×10<sup>-15</sup>m<sup>3</sup></b> | |
| - | + | ||
| - | + | ||
| + | <h2>5. Control volume selection</h2> | ||
| + | Note that product of the enzymatic reaction, AIP, is allowed to diffuse outside the cell. Hence, it is important to take into account the cell boundaries. It is worth considering whether diffusion or fluid movements will play a significant role. | ||
| + | <br/> | ||
| + | <p>Initially, we defined a control volume assuming that bacteria would grow in close colonies on the plate. We realized that our initial choice of control volume was not accurate, since our bacteria are meant to be used in suspension so we had to reconsider this issue. | ||
| + | <br/></p> | ||
This control volume is considered to be wrong, but the details were kept for reference.<br/> | This control volume is considered to be wrong, but the details were kept for reference.<br/> | ||
<br /> | <br /> | ||
| Line 65: | Line 73: | ||
<div class="accordionContent"> | <div class="accordionContent"> | ||
<b>Control volume initial choice</b><br/> | <b>Control volume initial choice</b><br/> | ||
| - | |||
The control volume: | The control volume: | ||
The inner boundary is determined by the bacterial cell (proteins after being displayed and cleaved cannot diffuse back into bacterium). The outer boundary is more time scale dependent. We have assumed that after mass cleavage of the display-proteins by TEV, many of these AIPs will bind to the receptors quite quickly (eg. 8 seconds). Our volume is determined by the distance that AIPs could travel outwards by diffusion within that short time. In this way, we are sure that the concentration of AIPs outside our control volume after a given time is approximately 0. | The inner boundary is determined by the bacterial cell (proteins after being displayed and cleaved cannot diffuse back into bacterium). The outer boundary is more time scale dependent. We have assumed that after mass cleavage of the display-proteins by TEV, many of these AIPs will bind to the receptors quite quickly (eg. 8 seconds). Our volume is determined by the distance that AIPs could travel outwards by diffusion within that short time. In this way, we are sure that the concentration of AIPs outside our control volume after a given time is approximately 0. | ||
| - | This approach is not very accurate and can lead us to false negative conclusions (as in reality there will be a concentration gradient, with highest | + | This approach is not very accurate and can lead us to false negative conclusions (as in reality there will be a concentration gradient, with highest concentration on the cell wall). |
<br /> | <br /> | ||
</html> | </html> | ||
| Line 96: | Line 103: | ||
</div> | </div> | ||
</div> | </div> | ||
| - | <br/><br/> | + | <br/><br/><br/> |
| - | |||
| - | |||
<b>Using CFU to estimate the spacing between cells</b><br/> | <b>Using CFU to estimate the spacing between cells</b><br/> | ||
CFU stands for Colony-forming unit. It is a measure of bacterial numbers. For liquids, CFU is measured per ml. | CFU stands for Colony-forming unit. It is a measure of bacterial numbers. For liquids, CFU is measured per ml. | ||
| Line 119: | Line 124: | ||
<br /> | <br /> | ||
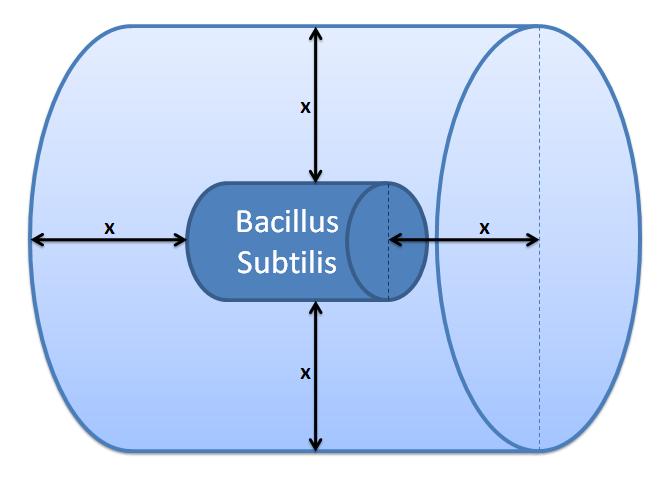
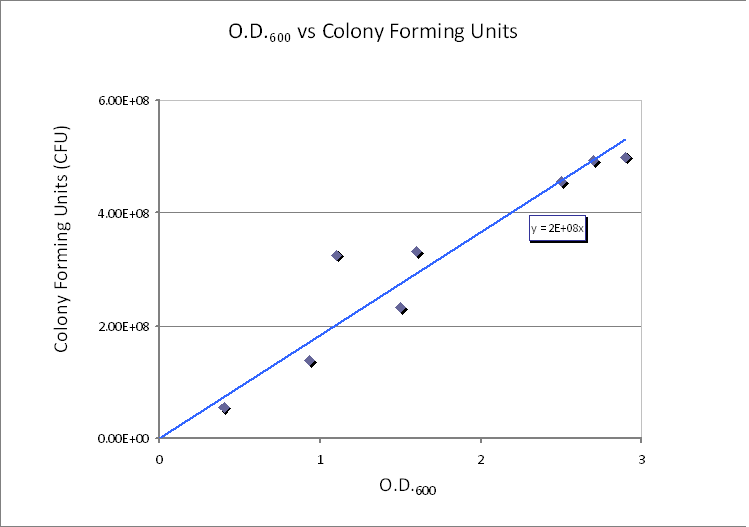
In this calculation, we assumed that only one cell will grow and become one colony (i.e. no more than one cell will form no more than one colony). Therefore, the maximum number of cells in 1ml of solution is 5×10<sup>8</sup>. Taking the volume of 1 ml = 10<sup>-3</sup> dm<sup>3</sup> and dividing by the (maximum) number of cells in 1ml gives the average control volume (CV) around each cell: 2×10<sup>-12</sup> dm<sup>3</sup>/cell. For simplicity, we choose the control volume to be cubic. Taking the third root of this value gives the length of each side of the control volume. | In this calculation, we assumed that only one cell will grow and become one colony (i.e. no more than one cell will form no more than one colony). Therefore, the maximum number of cells in 1ml of solution is 5×10<sup>8</sup>. Taking the volume of 1 ml = 10<sup>-3</sup> dm<sup>3</sup> and dividing by the (maximum) number of cells in 1ml gives the average control volume (CV) around each cell: 2×10<sup>-12</sup> dm<sup>3</sup>/cell. For simplicity, we choose the control volume to be cubic. Taking the third root of this value gives the length of each side of the control volume. | ||
| - | <p>Side length of | + | <p>Side length of cubic Control volume is y = 1.26×10<sup>-4</sup> dm = 1.26×10<sup>-5</sup> m.</p> |
<b>Choice of Control Volume allows simplifications</b><br/> | <b>Choice of Control Volume allows simplifications</b><br/> | ||
<CENTER><img src="https://static.igem.org/mediawiki/2010/7/7c/Enz_react11.png"/> </CENTER> | <CENTER><img src="https://static.igem.org/mediawiki/2010/7/7c/Enz_react11.png"/> </CENTER> | ||
<ul> | <ul> | ||
| - | <li>Firstly, assume that the cells will be placed in the centre of the CV. Hence, after cleavage the protein will have an average distance of y/2 to travel in order to cross the boundary of the CV | + | <li>Firstly, assume that the cells will be placed in the centre of the CV. Hence, after cleavage the protein will have an average distance of y/2 to travel in order to cross the boundary of the CV. Even if bacterium was not in the centre of CV and AIP had to diffuse across distance y, this is calculated using simplified 1 dimensional Fick's Law to happen within 0.01 ms. Hence, it will be almost instantaneous event for the concentration of AIPs around the cell to be uniform. Noticing that these time values are very small, we can approximate our model to have a uniform concentration across the volume. Since we are underestimating the value of AIP concentration right next to the cell's surface, we are overestimating the time required for the AIP concentration to reach the threshold level.</li> |
<li>We can neglect the diffusive fluxes across the CV border (see figure below). Assuming that adjacent cells are producing the peptide at the same rate and that the concentration of TEV is the same around the cell, then the fluxes should be of the same value giving a net flux of zero. Hence, we can neglect diffusion and have our model limited to one bacterium.</li> | <li>We can neglect the diffusive fluxes across the CV border (see figure below). Assuming that adjacent cells are producing the peptide at the same rate and that the concentration of TEV is the same around the cell, then the fluxes should be of the same value giving a net flux of zero. Hence, we can neglect diffusion and have our model limited to one bacterium.</li> | ||
</ul> | </ul> | ||
| Line 138: | Line 143: | ||
</div> | </div> | ||
<html> | <html> | ||
| - | |||
| - | |||
| - | |||
<br /> | <br /> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | <h2> | + | <h2>6. Localised concentrations</h2> |
| + | |||
| + | It was realised that for above choice of control volume the system would be unlikely to perform due to high concentration levels of TEV or Schistosoma proteases that would have been required. Hence, it was deduced that localised concentrations will play important role in this model. | ||
| + | <br/> | ||
| + | It was arbitrarily chosen that 20% to 50% of AIPs will bind to receptors rather than diffuse away. There is several arguments that would suggest this kind of percentage: | ||
| + | <ul><li> AIP being very close to cell surface will have equal chances of heading back towards bacterium as diffusing away from it as cell is way bigger than they are.</li> | ||
| + | <li>It is likely that there will be some chemical interactions between AIP and bacterium that could be attracting AIP to the host bacterium. Eg. electrostatic attraction is possible.</li> | ||
| + | </ul> | ||
| + | The percentage coefficient scales the AIP concentrations at the very end - after the ODE equations have been solved | ||
| + | |||
| + | <h2>7. Protein production</h2> | ||
<ul> | <ul> | ||
<li>The paper mentions that each cell displays 2.4×10<sup>5</sup> peptides. <a href="http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09188.x/pdf">[2]</a></li> | <li>The paper mentions that each cell displays 2.4×10<sup>5</sup> peptides. <a href="http://onlinelibrary.wiley.com/doi/10.1111/j.1574-6968.2000.tb09188.x/pdf">[2]</a></li> | ||
<li>2.4×10<sup>5</sup> molecules = 2.4×10<sup>5</sup>/6.02×10<sup>23</sup> mol = 0.398671×10<sup>-18</sup> mol</li> | <li>2.4×10<sup>5</sup> molecules = 2.4×10<sup>5</sup>/6.02×10<sup>23</sup> mol = 0.398671×10<sup>-18</sup> mol</li> | ||
| - | <li>Volume of B.sub: | + | <li>Volume of B.sub cell wall: 0.32×10<sup>-15</sup>m<sup>3</sup></li> |
<li>Concentration = [mol/L]</li> | <li>Concentration = [mol/L]</li> | ||
| - | <li>c = 1. | + | <li>c = 1.24×10<sup>-3</sup> mol/L. This is the concentration of protein that will be displayed on a single cell of B.sub. |
</ul> | </ul> | ||
<br /> | <br /> | ||
| - | Hence, we can deduce that the final concentration that the protein expression will tend to is: c = 1. | + | Hence, we can deduce that the final concentration that the protein expression will tend to is: c = 1.24×10<sup>-3</sup> mol/dm<sup>3</sup> = c<sub>final</sub>. |
<br /><br /> | <br /><br /> | ||
| - | Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards c<sub>final</sub>. | + | Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards c<sub>final</sub>. The degradation rate was kept constant (same as used in output amplification module), and the production rate was adjusted match the final concentration to be achieved. |
<br /> | <br /> | ||
Using a similar model to the simple production of Dioxygenase for the Output Amplification Model (<a href="https://2010.igem.org/Team:Imperial_College_London/Modelling/Output">Model preA</a>), we obtain the following graph: | Using a similar model to the simple production of Dioxygenase for the Output Amplification Model (<a href="https://2010.igem.org/Team:Imperial_College_London/Modelling/Output">Model preA</a>), we obtain the following graph: | ||
| Line 174: | Line 181: | ||
<html> | <html> | ||
<br /> | <br /> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<h2>References</h2> | <h2>References</h2> | ||
<ol> | <ol> | ||
| Line 200: | Line 188: | ||
<li>Gutenwik, J., Nilsson, B. & Axelsson, A. (2003) Determination of protein diffusion coefficients in agarose gel with a diffusion cell. Biochemical Engineering Journal. [Online] 19(2004), 1-7. Available from: http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6V5N-4B3MXDC-2-K&_cdi=5791&_user=217827&_pii=S1369703X03002377&_origin=search&_coverDate=07%2F01%2F2004&_sk=999809998&view=c&wchp=dGLzVtb-zSkzS&md5=c17d0e7320f03931006f9b1a10a438b9&ie=/sdarticle.pdf [Accessed August 20th 2010]</li> | <li>Gutenwik, J., Nilsson, B. & Axelsson, A. (2003) Determination of protein diffusion coefficients in agarose gel with a diffusion cell. Biochemical Engineering Journal. [Online] 19(2004), 1-7. Available from: http://www.sciencedirect.com/science?_ob=MImg&_imagekey=B6V5N-4B3MXDC-2-K&_cdi=5791&_user=217827&_pii=S1369703X03002377&_origin=search&_coverDate=07%2F01%2F2004&_sk=999809998&view=c&wchp=dGLzVtb-zSkzS&md5=c17d0e7320f03931006f9b1a10a438b9&ie=/sdarticle.pdf [Accessed August 20th 2010]</li> | ||
<li>Imperial College London (2008) Biofabricator Subtilis - Designer Genes. [Online] Available from: https://2008.igem.org/Imperial_College/18_September_2008 [Accessed 1st September 2010]</li> | <li>Imperial College London (2008) Biofabricator Subtilis - Designer Genes. [Online] Available from: https://2008.igem.org/Imperial_College/18_September_2008 [Accessed 1st September 2010]</li> | ||
| + | <li>Graham L. L. & Beverisge T. J. (1993) Structural Differentiation of the Bacillus subtilis 168 Cell Wall. Journal of Bacteriolofy. [Online] 5(1994), 1413-1420. Available from: http://jb.asm.org/cgi/reprint/176/5/1413?ijkey=27dafbac7e23dee50390d3fe67d9d1bab0c6f48c [Accessed October 26th 2010]</li> | ||
</ol> | </ol> | ||
</html> | </html> | ||
|} | |} | ||
Revision as of 16:51, 26 October 2010
| Modelling | Overview | Detection Model | Signaling Model | Fast Response Model | Interactions |
| A major part of the project consisted of modelling each module. This enabled us to decide which ideas we should implement. Look at the Fast Response page for a great example of how modelling has made a major impact on our design! | |
| Objectives | Description | Results | Constants | MATLAB Code |
| Detailed Description | ||
This model consists of 5 parts that had to be developed:
1. Elements of the system
2. Interactions between elementsApart from the proteins being expressed from genes, there was only one more chemical reaction identified in this part of the system. This is the cleavage of proteins, which is an enzymatic reaction:
 This enzymatic reaction can be rewritten as ordinary differential equations (ODEs), which is of similar form as the 1-step amplification model. However, most of the constants and initial concentrations are different.  3. Threshold concentration of AIPThe optimal peptide concentration required to activate ComD is 10 ng/ml [1]. This is the threshold value for ComD activation. However, the minimum concentration of peptide to give a detectable activation is 0.5ng/ml.The threshold for the minimal activation of the receptor is cth=4.4658×10-9 mol/L. Click on the button below to uncover the calculations. Converting 10 ng/ml to 4.4658×10-9 mol/L
4. Cell Wall VolumeThe volume of the cell wall was necessary to be calculated for calculation of concentrations in enzymatic reaction.Volume of B. subtilis is 2.79μm3 and the thickness of cell wall is 35nm [5]. In order to approximate the cell wall volume assume that B. subtilis is a sphere - not a rod. Calculate the outer radius from the total volume: 0.874μm. Now subtract the thickness of cell wall from outer radius to determine inner radius of the sphere: 0.839μm. The volume of cell wall equals to the difference between outer volume and the inner volume (calculated from inner radius): cell wall volume=0.32×10-15m3 5. Control volume selectionNote that product of the enzymatic reaction, AIP, is allowed to diffuse outside the cell. Hence, it is important to take into account the cell boundaries. It is worth considering whether diffusion or fluid movements will play a significant role.Initially, we defined a control volume assuming that bacteria would grow in close colonies on the plate. We realized that our initial choice of control volume was not accurate, since our bacteria are meant to be used in suspension so we had to reconsider this issue.
Initial Choice of Control Volume
Control volume initial choice
The control volume: The inner boundary is determined by the bacterial cell (proteins after being displayed and cleaved cannot diffuse back into bacterium). The outer boundary is more time scale dependent. We have assumed that after mass cleavage of the display-proteins by TEV, many of these AIPs will bind to the receptors quite quickly (eg. 8 seconds). Our volume is determined by the distance that AIPs could travel outwards by diffusion within that short time. In this way, we are sure that the concentration of AIPs outside our control volume after a given time is approximately 0. This approach is not very accurate and can lead us to false negative conclusions (as in reality there will be a concentration gradient, with highest concentration on the cell wall).
Using CFU to estimate the spacing between cells CFU stands for Colony-forming unit. It is a measure of bacterial numbers. For liquids, CFU is measured per ml. We already have data of CFU/ml from the Imperial iGEM 2008 team, so we could use this data to estimate the number of cells in a given volume using a spectrometer at 600nm wavelength. The graph below is taken from the Imperial iGEM 2008 Wiki page [4].
Side length of cubic Control volume is y = 1.26×10-4 dm = 1.26×10-5 m. Choice of Control Volume allows simplifications
6. Localised concentrationsIt was realised that for above choice of control volume the system would be unlikely to perform due to high concentration levels of TEV or Schistosoma proteases that would have been required. Hence, it was deduced that localised concentrations will play important role in this model.It was arbitrarily chosen that 20% to 50% of AIPs will bind to receptors rather than diffuse away. There is several arguments that would suggest this kind of percentage:
7. Protein production
Hence, we can deduce that the final concentration that the protein expression will tend to is: c = 1.24×10-3 mol/dm3 = cfinal. Therefore, we can model the protein production by transcription and translation and adjust the production constants so that the concentration will tend towards cfinal. The degradation rate was kept constant (same as used in output amplification module), and the production rate was adjusted match the final concentration to be achieved. Using a similar model to the simple production of Dioxygenase for the Output Amplification Model (Model preA), we obtain the following graph:
References
|
 "
"