From 2010.igem.org

Octrees

Overview

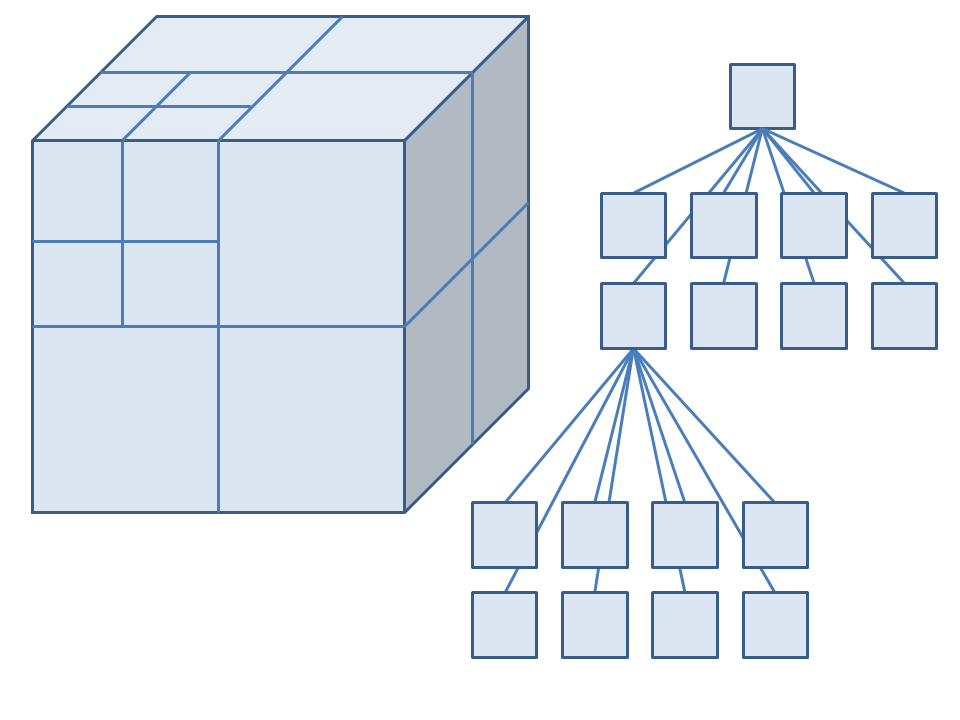
The octree is a tree type data structure. This a hierarchical data structure comprised of nested nodes. Each node has one parent and either eight or zero children. Nodes with zero children are called leaves. A node's children subdivide the volume of their parent into eight smaller volumes. Figure 1 shows how an octree partitions space into smaller and smaller volumes and how this can be represented by a tree data structure.

Fig. 1. Schematic illustration of how an octree subdividies in space (left) and how this is represented as a node and leaf data structure (right). In this example the highest resolution node is of depth 3.

Methods

Each node stores the quantity of chemical and the diffusivity constant for its field. Nodes know what depth they are inside the octree structure and which nodes are their neighbours. This is re-computed each time a node is split it is necessary to know who your neighbors are in order to compute the diffusion of chemicals through the field from one node to those spatially adjacent (i.e. not necessarily nodes of the same parent).

To be able to perform operations across an octree data structure it is necessary to use a traversal algorithm. This is an algorithm that visits each node. There are many different ways of doing this, the method used in BSim is the ‘full post-order’ traverse. This visits each node from deepest depth first, then the second deepest etcetera until it reaches the parent node.

PostOrderTraverse(Node)

{
    IF(Node != leaf){
        FOR(i=0:8){
        PostOrderTraverse(Node.subNodes[i])}
        VISIT(Node)
   }

}

Splitting the Octree

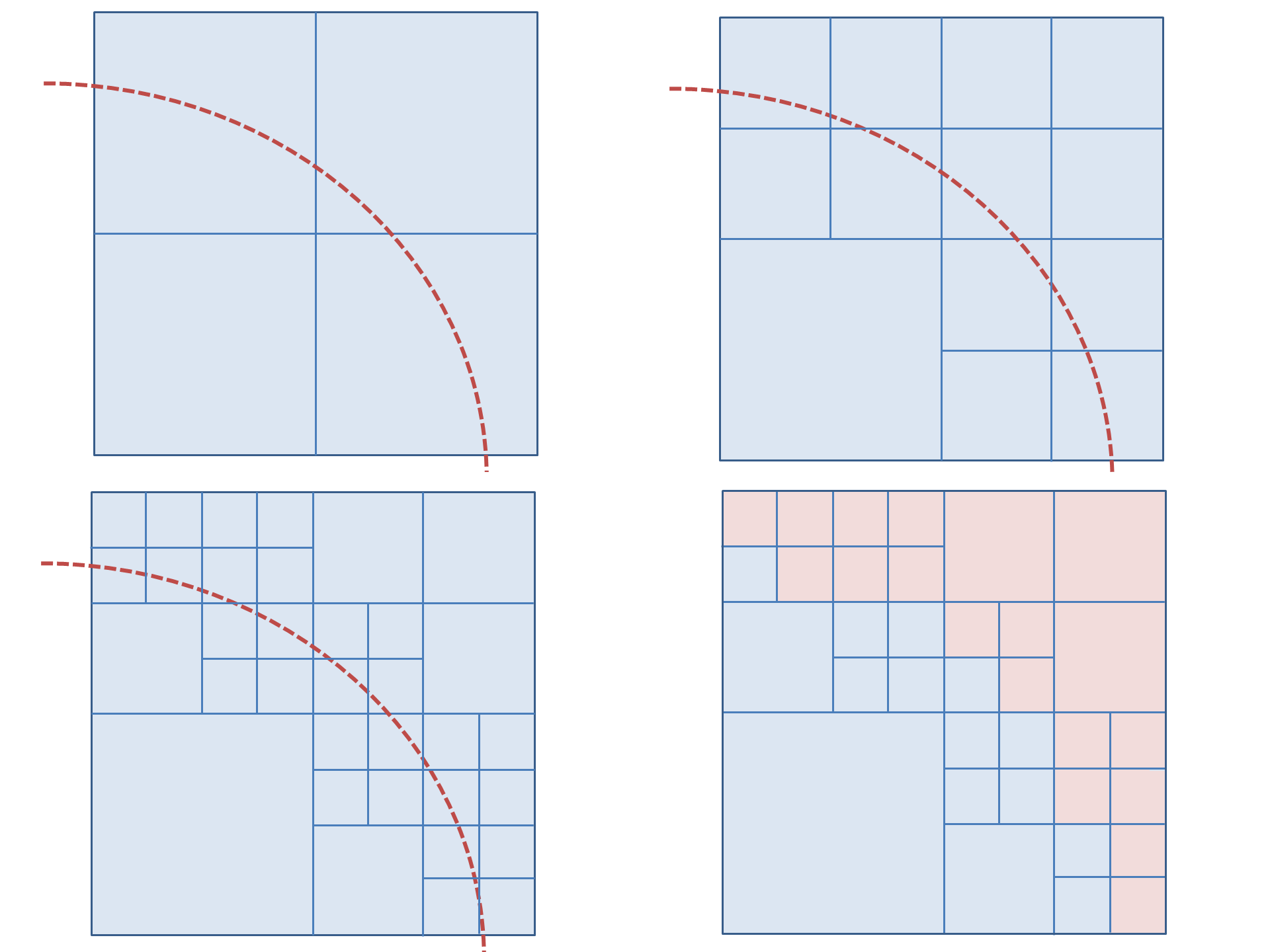
The octree data structure is used for holding and computing the chemical field because it is able to approximately represent fields of arbitrary shapes. This is done by splitting an octree from a parent node around a mesh shape. It is easier to explain in terms of the two dimensional quadtree,

Fig. 2. An example of quadtree partitioning, as the maximum depth increases, the partition more closely approximates the curve

This example has a maximum depth of three, the example of an octree partition in fig. 2 has a depth of 5. The maximum resolution increases exponentially with depth, a depth of 7 appears to be adequate for reasonably complex shapes, e.g. the mesh of a gel strand.

The algorithm for splitting the octree around a mesh is relatively simple. It uses the post order traverse function above to access each octree node from the bottom to the top. The following function would be in place of the ‘VISIT’ command:

FOR each Edge of Mesh{
   FOR each Edge of Node{
     IF(Node Edge is crossed by a Mesh Edge)
       Divide Node into SubNodes
     ELSE
       Check next Mesh Edge
   }
}

It is relatively inefficient, each edge of the octree is tested against each edge of the mesh. It could be optimised to try and exclude mesh edges that are extremely unlikely to cross the node edge. It would also be prudent to exclude mesh edges that are too far away from the node to intersect it, as this algorithm would require only addition and subtraction, whereas the collision detection algorithm operates with vector products.

An example of how an octree is split around a mesh in BSim can be seen in the video below. Here you can see how the octree structure looks at each stage of its generation. The maximum resolution increases from 1 at the start, to 8 in the final frame.