Team:St Andrews/project/modelling/model 3
From 2010.igem.org
(→Implementation) |
(→Implementation) |
||
| Line 71: | Line 71: | ||
[[Image:Snapshot 2010-10-26 12-43-47.jpg]] | [[Image:Snapshot 2010-10-26 12-43-47.jpg]] | ||
| + | |||
| + | From these plots we can clearly see that by increasing the HSL conversion rate we also decrease the bistability of the system and by increasing the HSL degradation rate we increase the bistability of the system. | ||
=Conclusions= | =Conclusions= | ||
Revision as of 11:47, 26 October 2010


Model 3: Pseudo Multi Cell One Dimension
Contents |
Theory & assumptions
The results produced from both of our previous models were unsatisfactory, since neither gave us quantifiable data from which experimental comparisons could be made, although the switching on was clearly visible in both. Therefore it was decided that in order to properly capture the mechanism of bistability it was essential to have some element of cell number, and as such we must simulate the growth of a cell colony rather than artificially increase the amount of HSL in our external environment. Several crucial elements were added to the model to incorporate this new outlook:
i. A new variable 'Number of cells' was added
ii. Two new functions which simulate cell growth and cell death
iii. A new paramter 'Volume'
The number of cells is set at the beginning of the simulation by the user. Based on a doubling time of 20 minutes, the variable is increased every increment by the cell growth function. In order to simulate the increase in HSL due to these new cells, each new cell is accompanied by an increase in HSL which is equal to that being contributed by the cells already present in the system. (VOLUME THING IN DIFFERENTIALS). Similarly we included a cell death function which decreases the number of cells at a halving rate of 20 minutes in tandem to the growth rate.
Results
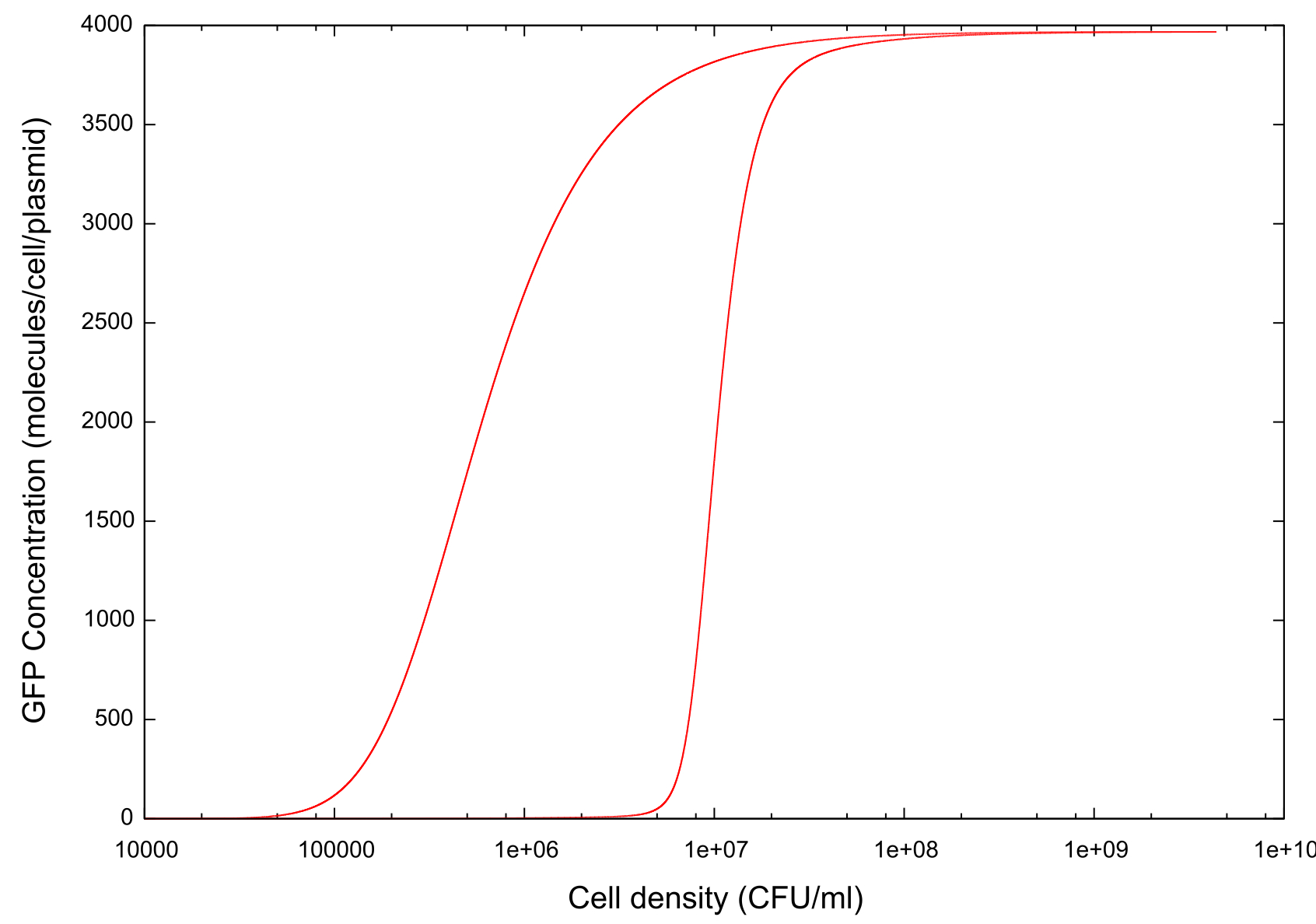
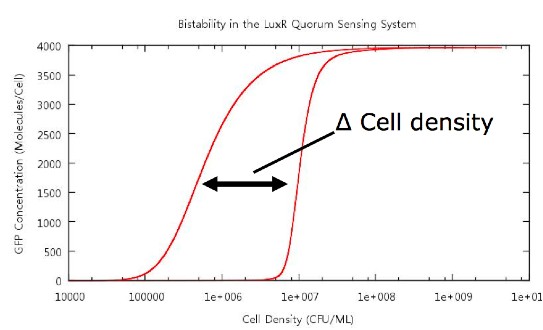
On running the model through the cell growth, stationary and cell death phases, the first example of ‘true bistability’ is produced, see figure . Since this model contains spatial dimensions we are able to determine a specific cell density at which the switch happens, and this is comparable to the value predicted by other models and by experimental evidence. There is also a clear difference between the switch-on and switch-off thresholds which we hypothesise is caused by…
Figure 1: Graph showing change in GFP concentration against cell density
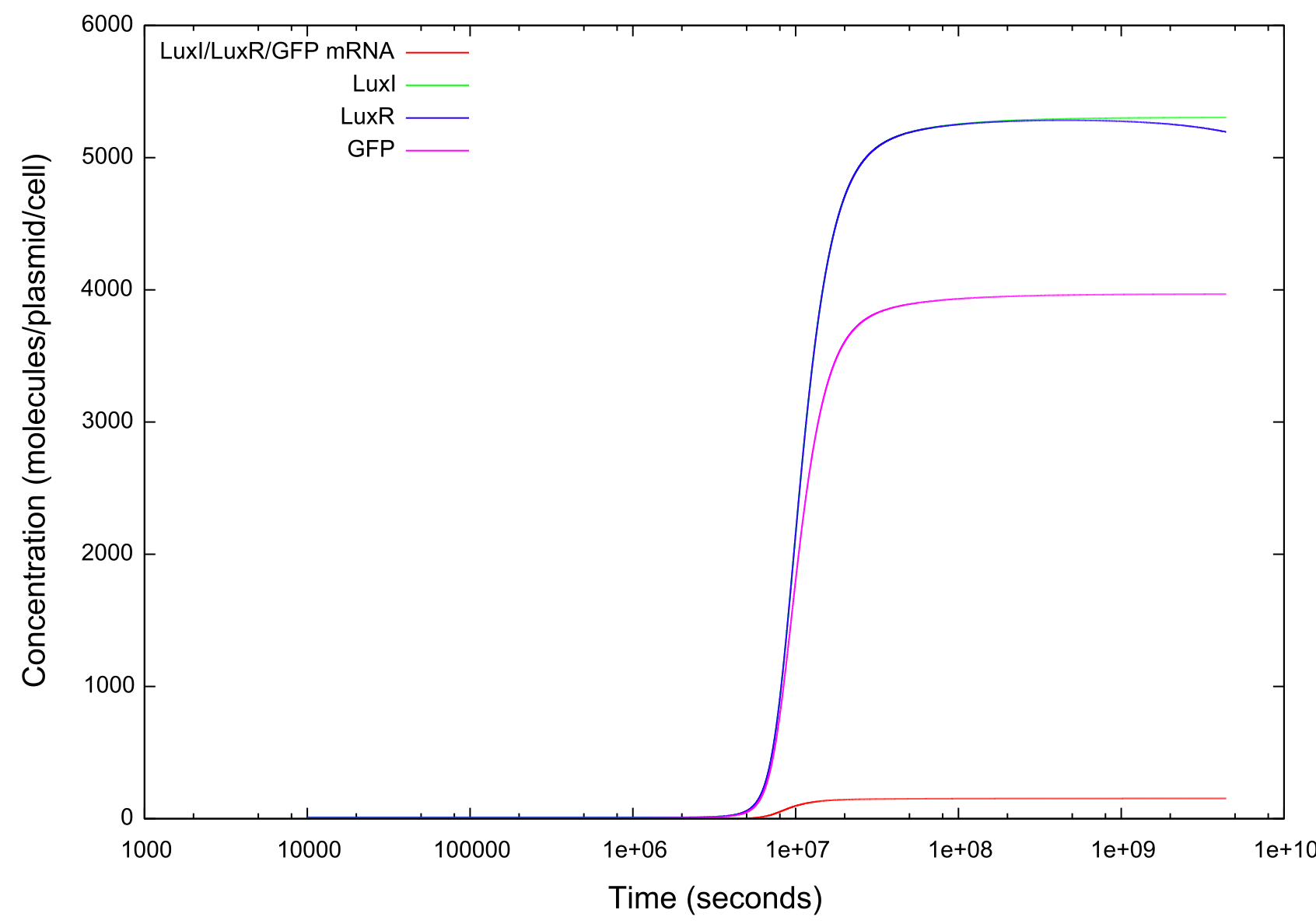
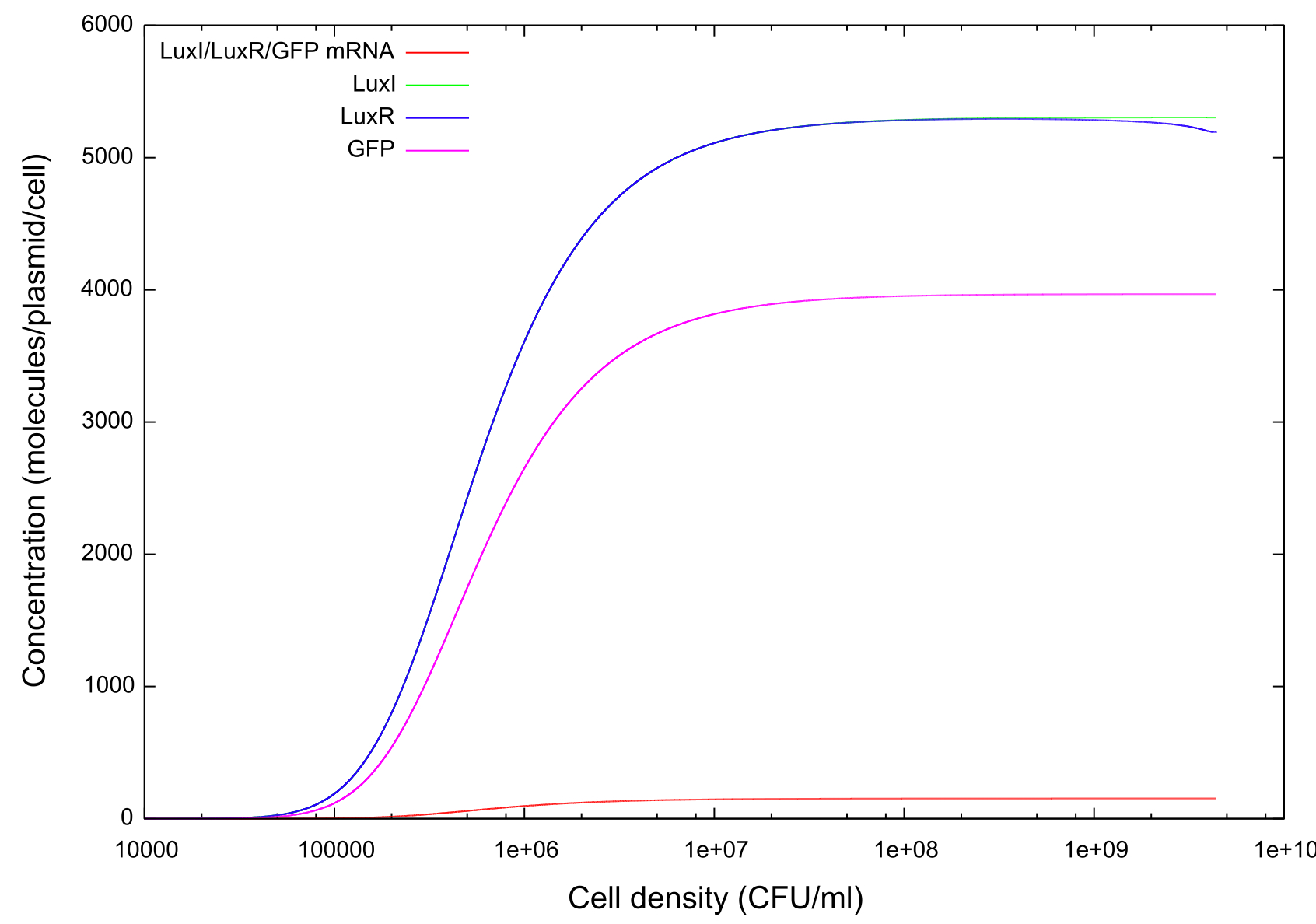
Info on HSL-LuxR concentration behaviour
Graph with up and down data?
Parameter Testing
The next stage in the development of our model was to probe which factors had an impact on the behaviour of the system and exactly what that impact was and what implications they have.
Measuring bistability
The key point which we wished to investigate was the bistability of our system, so in order to do this we had to develop a standard way in which we would measure the 'level' of bistability. The method decided upon was to take a reading of the cell density at a fixed value of GFP concentration during cell growth and similarly record the cell density at the same GFP concentration during cell death. Thus we would obtain a value Δ Cell density which gives us a useful quantity which we can use in our tests.
Testing our switch
We decided that there were some key parameters which we would like to test, which were the rates of:
- Association and dissociation
- HSL production and degradation
- LuxR degradation
- Promoter binding site strengths
Implementation
In order to test the level of bistability, we first needed to find the parameter range for which the system switched on. This was done by running our model many times with different values of the parameter we wished to investigate, and looking at for which values the system switched on by the final concentration of GFP. We could then operate only within the operating range of the switch and run our model many times within this range, looking at the value of ΔCell density and comparing for different parameter values.
HSL production & degradation
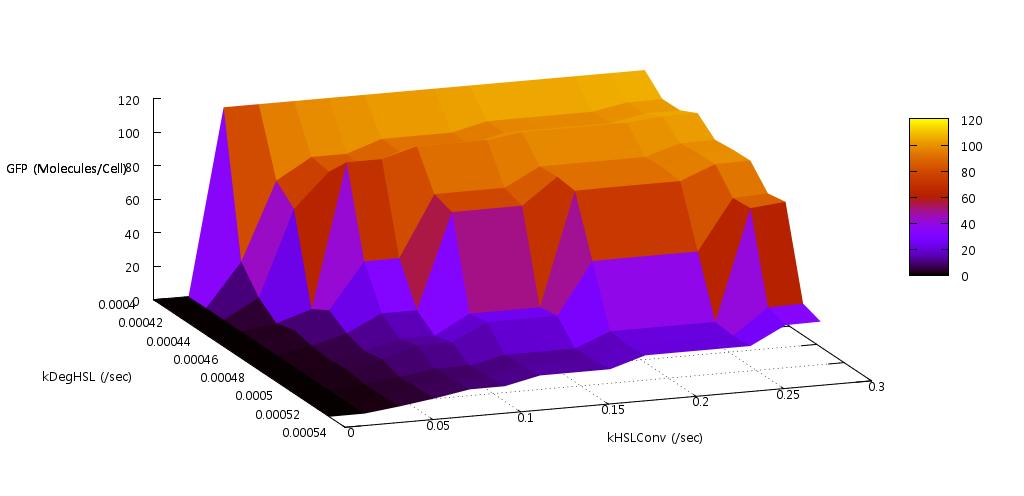
We reasoned that the rate at which HSL was both produced, and degraded within the system should have a significant effect on the bistability since this molecule is fundamental to the process of quorum sensing in E.coli. Indeed our initial tests found that if the conversion rate was too low, or the degradation rate too high, the system did not actually switch on (see figure ).
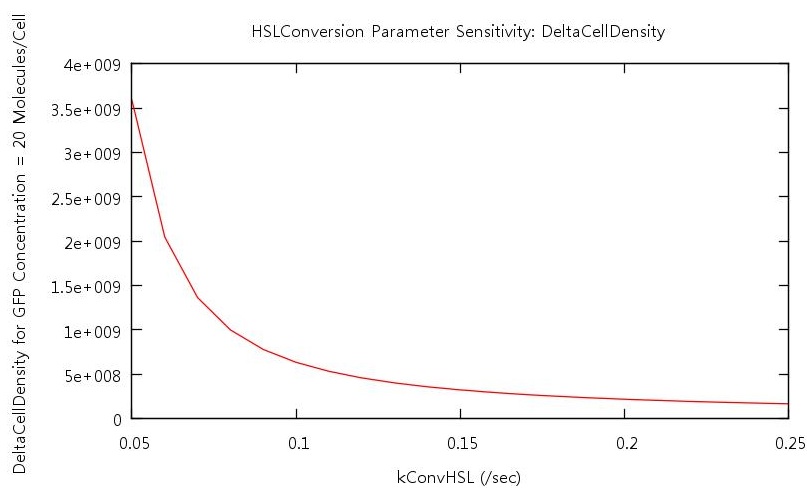
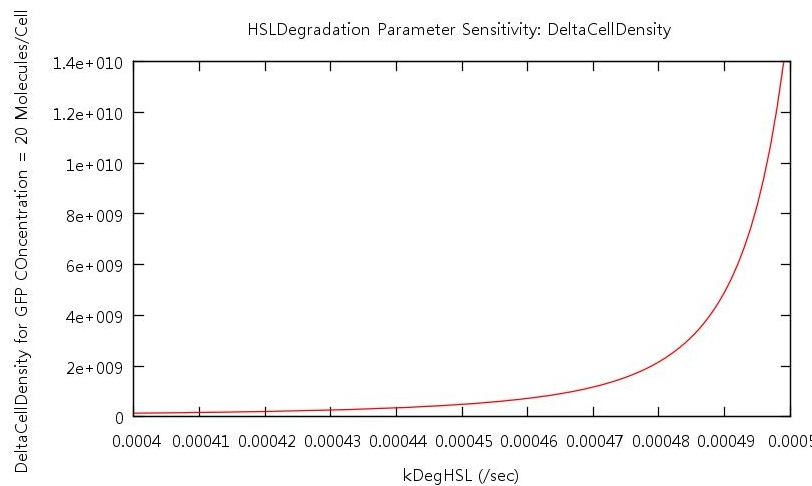
Our test indicated that our parameter test should be performed for values, 0.05 < kConvHSL < 0.25 and 0.0004 < kDegHSL < 0.0005. The results of these tests are shown below.
From these plots we can clearly see that by increasing the HSL conversion rate we also decrease the bistability of the system and by increasing the HSL degradation rate we increase the bistability of the system.
 "
"