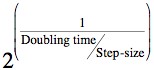Team:St Andrews/project/modelling/model 3/growthdeathfunctions
From 2010.igem.org


Cell Growth & Death Functions
Rather than artificially change the concentrations of HSL in the system, either by manually adding it or taking it away, we felt it would be more sensible and ultimately more biologically realistic to simulate the physical growth and subsequent death of a cell population. This was practically implemented in our code by creating two functions, "CellGrowth" and "CellDeath"
Cell Growth
Biologically we made the assumption that a population of E.coli cells will double every 20 minutes, which is accepted as a typical doubling time for that particular species. The function then simply takes the number of cells and multiplies it by a value determined by our doubling time and the step size chosen for the Runge-Kutta solver. So the formula for calculating the multiplication constant is:
void CellGrowth(double y[]){
y[9] *= 1.00001444067053;
}
Thus each time the function is called, the number of cells is multiplied by the output of this relationship, simulating the growth of a cell population over time.
Cell Death
Similarly we created a cell death function to simulate the decline in the number of cells within a population. While we had no reliable information on the death rate, it was assumed that a value equal to the growth rate would be a fair assumption. Thus the function "CellDeath" simply divides the number of cells by a constant depending on the step-size.
void CellDeath(double y[]){
y[9] /= 1.00001444067053;
}
The growth cycle
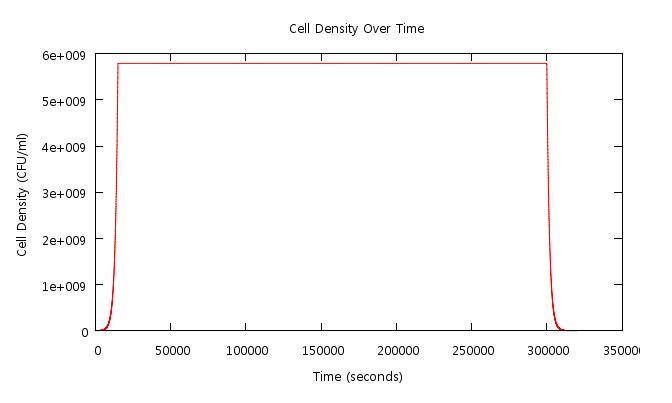
The only factor left to decide is for how long the cell growth and cell death phases should take place. In our models, we ran the growth phase for N increments, held the cells at a fixed number to allow concentrations to equilibrate, then ran the cell death phase until the system switched off again. Graphically this can be represented.
It should be noted that the plot is of cell density rather than cell number, since in this model an element of spatiality was introduced, which is explained here.
 "
"