Team:Peking/Modeling/Advanced Model
From 2010.igem.org
| Line 10: | Line 10: | ||
<br><br> | <br><br> | ||
<font size=6><font color=#585858><font face="Franklin Gothic Demi Cond"> Advanced Model</font></font></font> | <font size=6><font color=#585858><font face="Franklin Gothic Demi Cond"> Advanced Model</font></font></font> | ||
| - | <br><br> | + | <br><br><br> </html> |
| + | [[Team:Peking/Modeling|Modeling]] > [[Team:Peking/Modeling/Advanced_Model|Advanced Model]] <html> | ||
</div> | </div> | ||
Revision as of 11:19, 27 October 2010

As the IOA function still cannot work well to ensure the linear relationship when the input range spans several orders of magnitude, we search for semilog networks further using the same calculation and data-analyzing method. Semilog represents that the output and LOG(input) fit linear relationship, different from IOA in x axis in Figure 1.
Identifying Minimal Semilog Networks
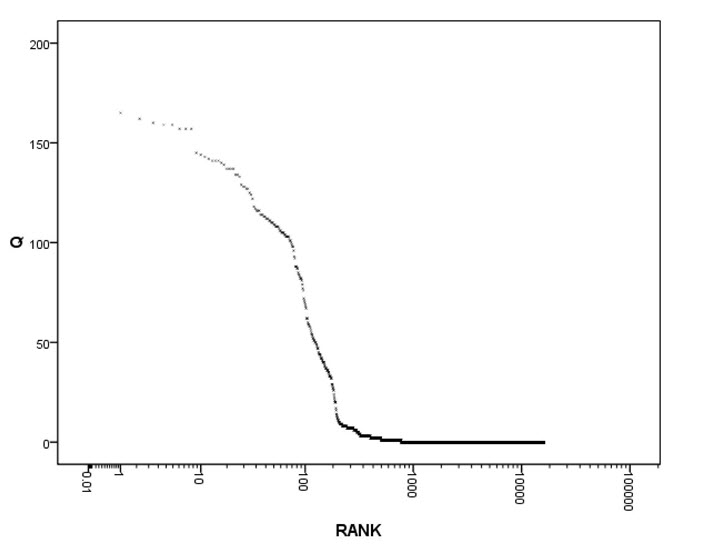
We again get the Q-Rank Figure. Topologies that have large Q value are still the minority.(Figure 14)
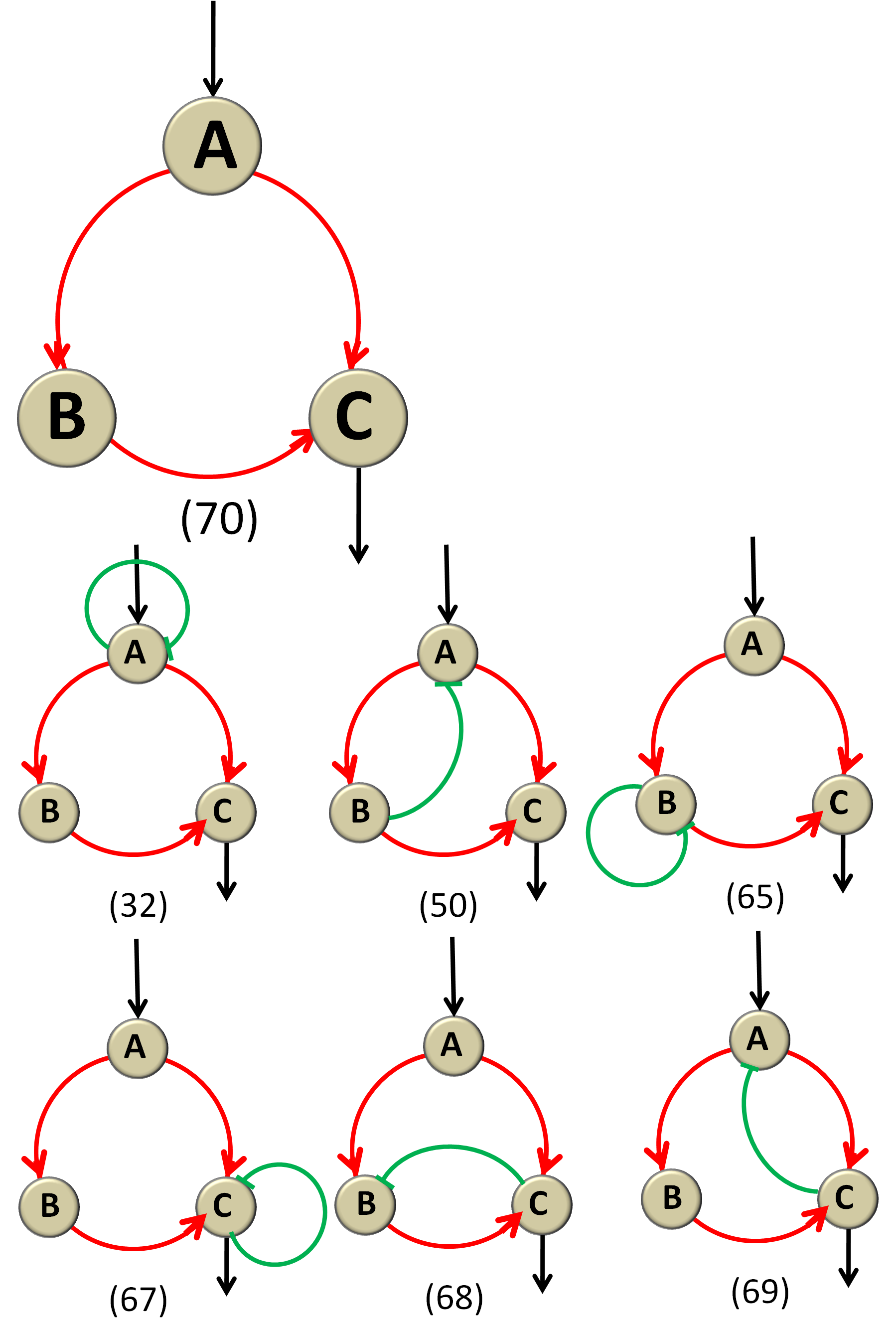
Listed in Figure 15 are all the simplest topologies whose Q value is above 100 that have 4 or less direct links between the three nodes. There are only one 3-link topology( as the 7th topology in Figure 15) out of all the 7 simplest topologies, and it has exactly the common features of the seven topologies: two positive controls from A node to respectively B node and C node, and one positive control from B to C. We call it the All Activated Network(AAN). The role of different nodes and links will be discussed in the next part.
Figure 14 The Q value network topologies SequenceWe sort in reverse sequence all the network topologies according to their Q value. X Axis is their ranks, while Y Axis is their corresponding Q values.
Figure 15 All Functional NetworksThe numbers below each network are their ranks. The bigger topology has 2 links while the other 6 networks have 3 links. In each network, the green arc with one short straight line at one end stands for repression from the start node to the end node and the red arc with one arrow at one end stands for activation.
[TOP]
Mechanisms of Minimal Semilog Networks and Key Parameters Analysis
In order to unravel the mechanism that AAN functions, we analysis the topology with the ODE equations, and we also get the key parameters in this part.
When the network reaches its steady state,
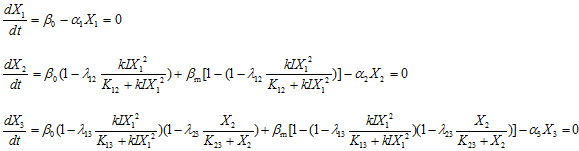
Solve the equations,
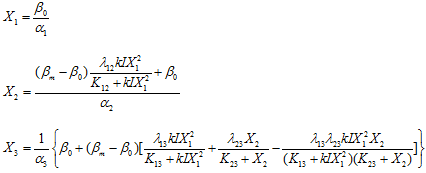
When![]() , there is
, there is
![]() ,so:
,so:
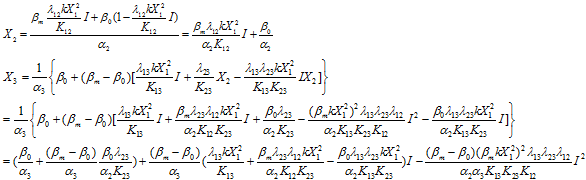
As to the object function![]() , we adopt the method of Taylor expansion
, we adopt the method of Taylor expansion
![]()
Then we can see that the transform of ![]() fits well with the transform of the object function.
fits well with the transform of the object function.
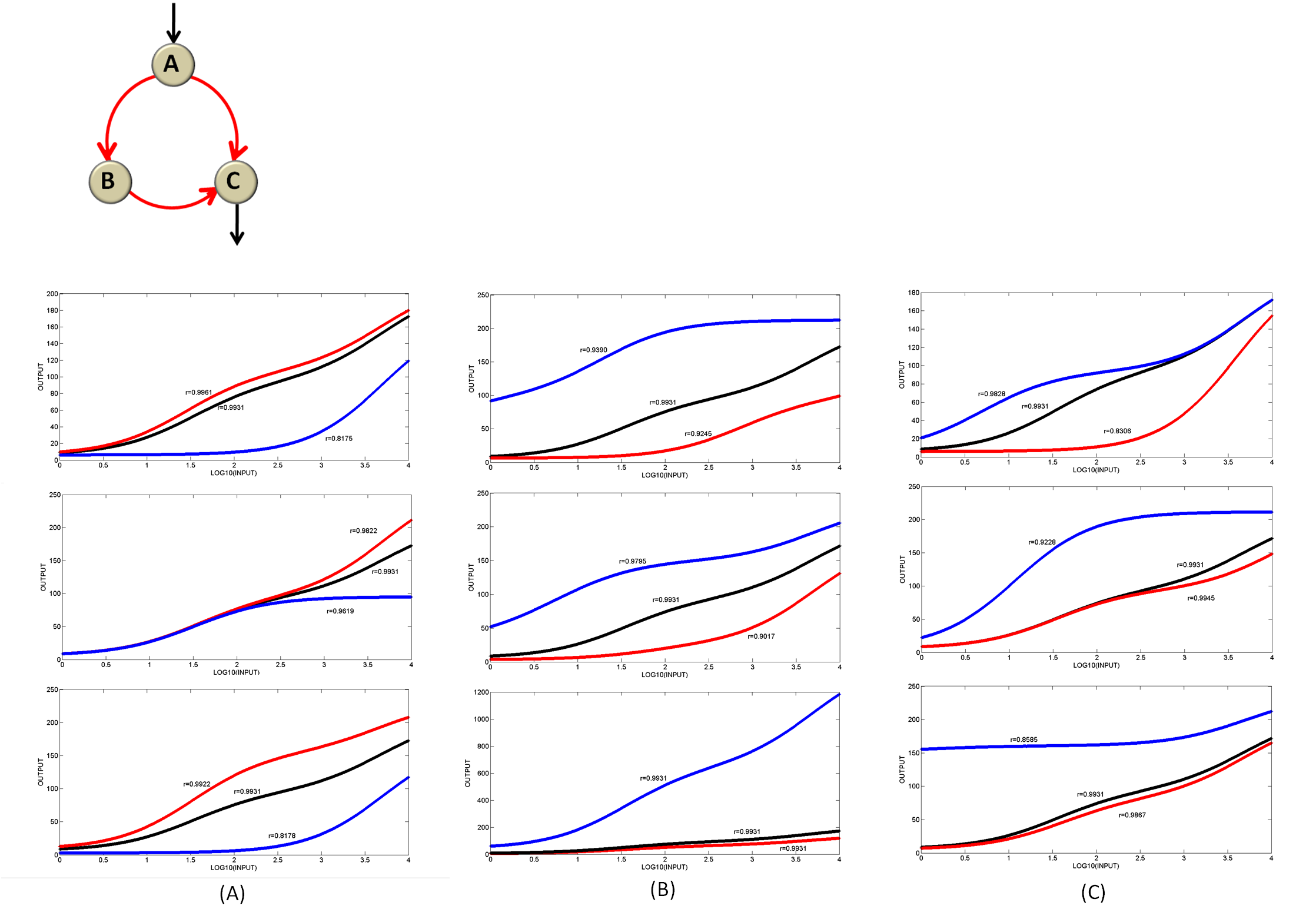
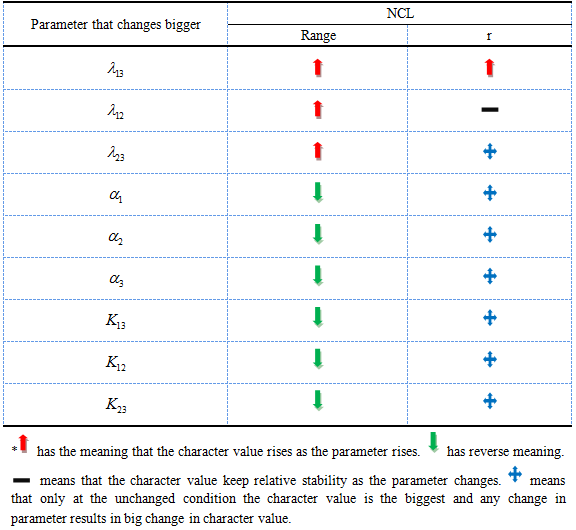
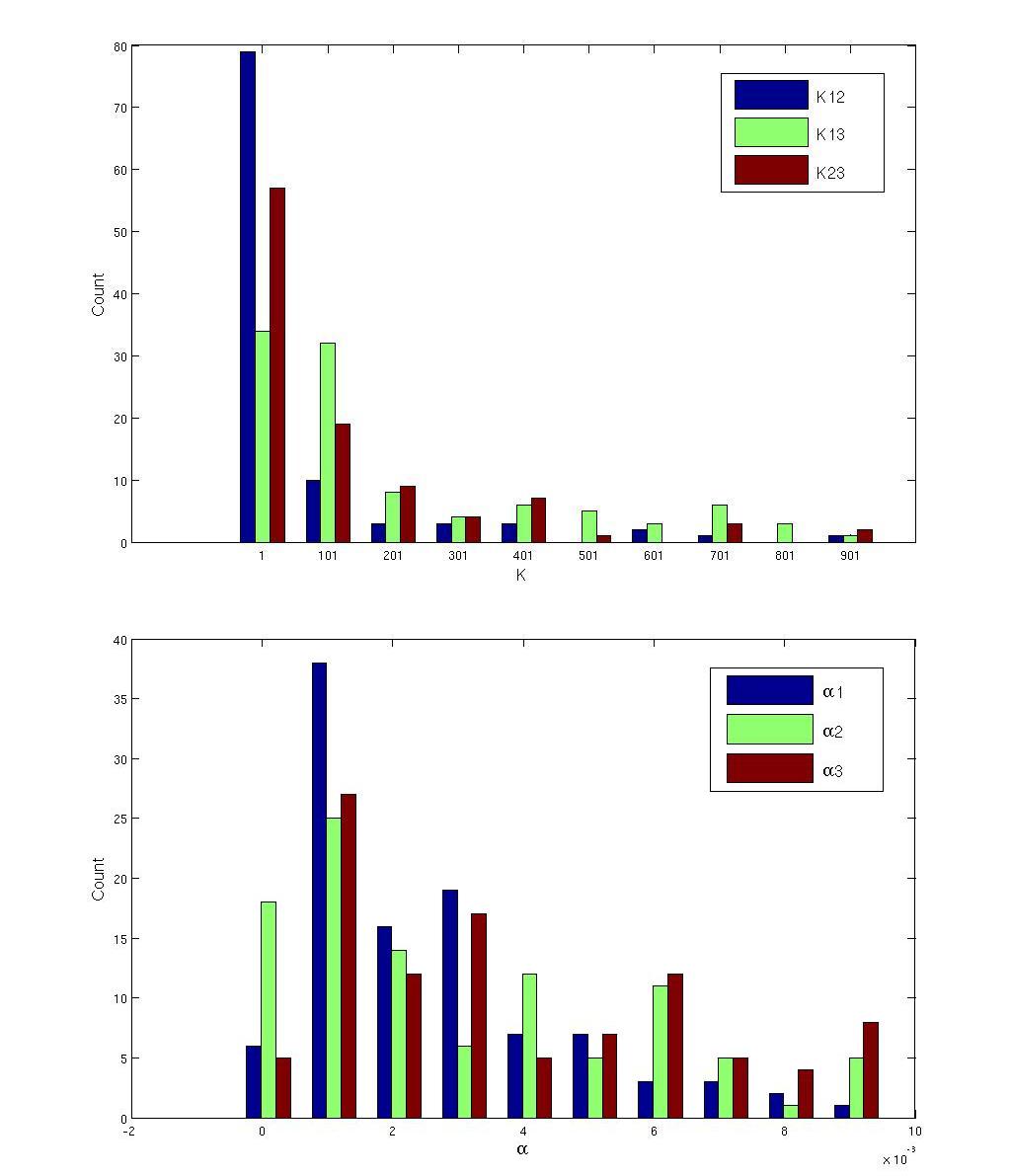
Known the reason why the topology is functional in the object function, we need to analysis for the most important parameter in order to provide theoretical support for practice (Figure 16). We also list the parameter changes in Table 3. Among the nine parameters, the essential parameter for the output range is not obvious and that for r is the same condition – we can only see that ![]() has no influence on r. Based on an overall consideration, we suggest that in practice a smaller
has no influence on r. Based on an overall consideration, we suggest that in practice a smaller ![]() , a larger
, a larger ![]() and a larger
and a larger ![]() should be adopted.
should be adopted.
Figure 16 Analysis for key parametersWe got all functional sets of parameters of AAN and selected randomly one set and processed it with Matlab to compare the differences once the parameters change. When analyzing one parameter, we only change this very parameter and keep others the same, and when we change the parameter to a lower level, we get the blue line, when to a higher level, we get the red line and the black line is for the unchanged parameter set. Each line has its Pearson Correlation Coefficient r marked in the figure. The X Axis is the concentration of Hg ion as INPUT whose range is 1 to 10000 nM, and the Y Axis is the concentration of node C with the unit of nM. (A) We analyze ![]()
![]()
![]() from top to bottom. (B) the degradation rate of node A , B and C, respectively,
from top to bottom. (B) the degradation rate of node A , B and C, respectively,![]()
![]()
![]() (C) The dissociation rate for each link:
(C) The dissociation rate for each link:![]()
![]()
![]() .
.
Table 3 The change of two important characters as the parameters rise
[TOP]
Parameters Tendency of the Semilog Networks
It can be seen from the distribution of K and α values that compared to networks with linear response curve, single parameter shows much less tendency. Instead, to establish a semi-log response curve may require the cooperation of multiple parameter values.
[TOP]
Analysis of All Possible Three-Node Networks
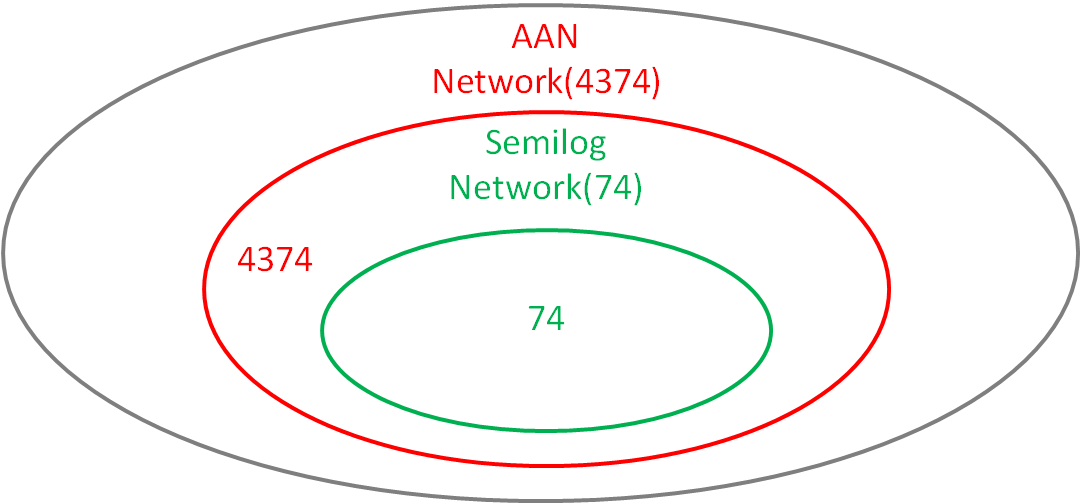
Again through the analyses above, we only know that AAN can be functional in Semilog function, but whether the topology is necessary among the more complex networks are still unknown, so we analysis all of the first 74 topologies (Q>100) that are well capable of the Semilog function.(Figure 18)
Figure 18 Analysis of the first 160 networks We count all ANNs and the Semilog networks whose Q value is above 100, and discover that all of the Semilog networks are make up of the ANN topology and the topologies contain it.
Analysis of these robust topologies shows that they all contain AAN, so that the very topology is necessary for Semilog function.
[TOP]
Motif Combinations that Improve Semilog Linear
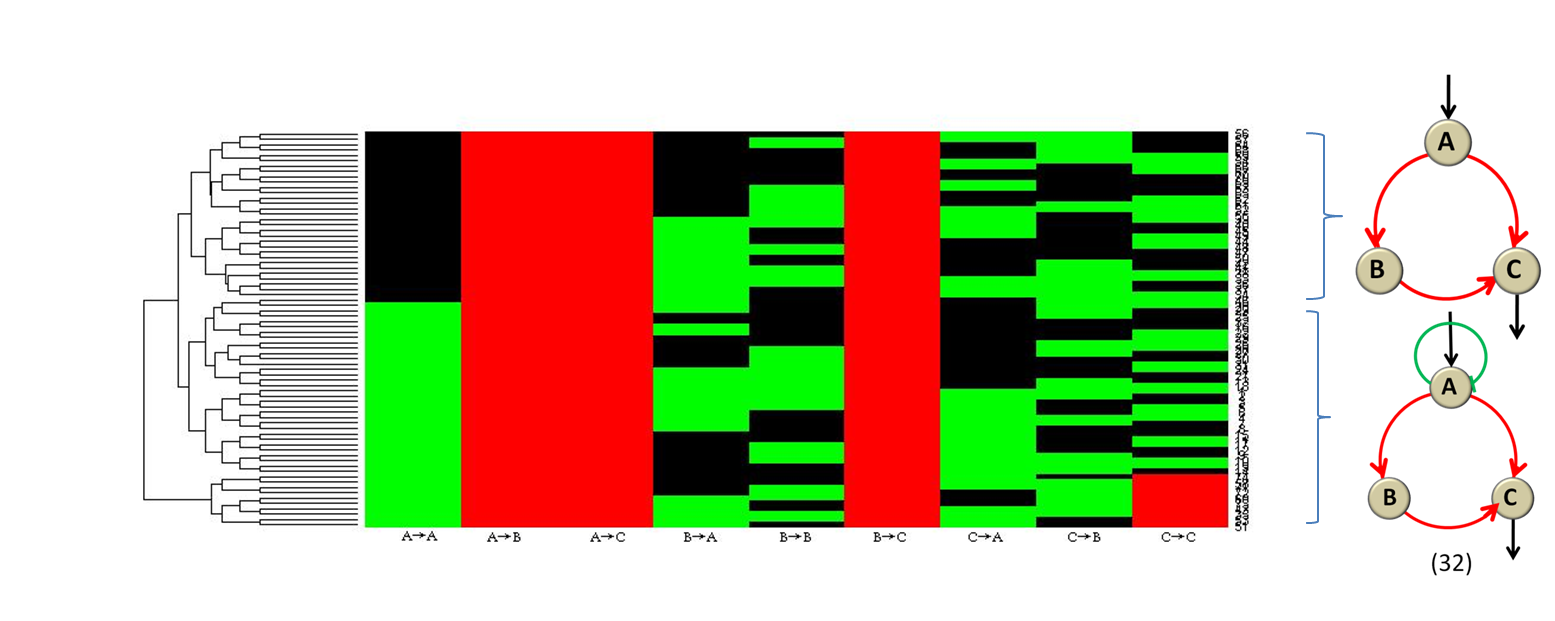
To investigate what additional features can improve the functional performance in some more complex and more robust networks than minimal topologies, we clustered the first 74 networks.(Figure 19)
Figure 19 The clustergrams of the networksWe use the clustergram command in matlab to get the additional features of the functional networks. The nine vertical rectangle bar stand for nine links in Figure 2 which are, respectively, from A to A, from A to B, from A to C, from B to A, from B to B, from B to C, from C to A, from C to B, from C to C. And red stands for activation, green for repression and black for no regulation. The topologies on the right are corresponding minimal topologies that is shown in the clustergrams on the left.
The results clearly indicate that apart from the link from A to B, from A to C, from B to C, and from C to C, there should be no positive regulation.
[TOP]
Advandced Part Summary
Hence, we finally get the practical form of genetic circuits that can be adopted by our wetlab part. And the mechaism and parameter preferences are understood to some extent. And part of the bioreporter wetlab was designed according to the results our modeling got. What's more, using the same calculation and analysing method as shown above, we can search for more functional genetic circuits further on, apart from Linear and Semilog Linear. So the designation of wetlab is theoretically supported.
[TOP]
 "
"