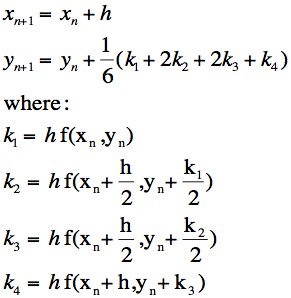Team:St Andrews/project/modelling/models/RK4
Foruth Order Runge-Kutta Method
Introduction
Our method of solving differential equations is based on Fourth Order Runge-Kutta Method. This technique is the most widely used way of numerically solving differential equations and various methods of implementation were looked at. Most of our coding has been based on the work of Aberdeen 2009 iGEM team who used the same method in their modelling. We would like to thank the team for their work and making it available to others like us for future use.
Mathematical basis
While the strict mathematical derivation of the Runge-Kutta method is available( see [http://www.ss.ncu.edu.tw/~lyu/lecture_files_en/lyu_NSSP_Notes/Lyu_NSSP_AppendixC.pdf here for details] ), we omit it here and instead give a brief explanation of the principles behind the technique.
There are several key formulae in the 4th Order Runge-Kutta algorithm, which are:
The iteration of the x-values is done very simply adding a fixed step-size (h) at each iteration, thus resulting in a constant increase in the x-value according to the value of h chosen for a particular purpose.
The y-value iteration contains a much more elegant set of relationships. It should be clear to you that the y-iteration formula is in fact a weighted average of the four value k values, k1, k2, k3 and k4. Even at a first glance it should also be apparent that a 'weight' of 2/6 is given to k2 and k3 while a smaller weighting of 1/6 is attributed to k1 and k2. What then do these k-value correspond to geometrically?
Look first at k1. It is equal to the function f(xn,yn) multiplied by the step-size h, which is just the Euler prediction for Δy. It is the vertical distance from the previous point to the next Euler predicted point.
Then consider ksub>2</sub>. It should be noted that the x-value at which the function is being evaluated is half-way across the prediction interval and the y-value consists of the current y-value plus half of the Euler predicted Δy.
 "
"