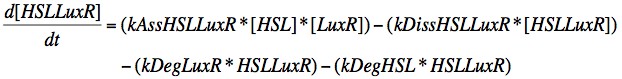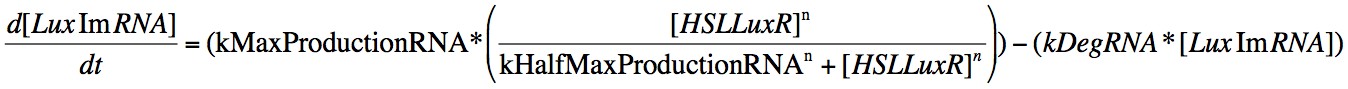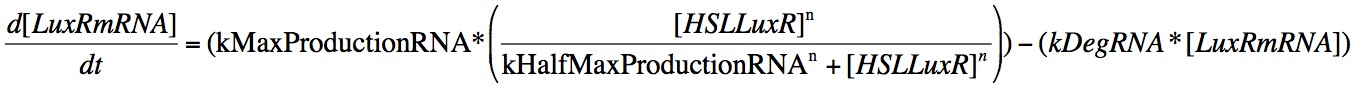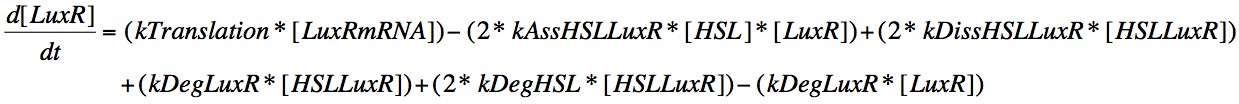Team:St Andrews/project/modelling
Modelling
Contents |
Introduction
Hello and welcome to the St. Andrews iGEM 2010 modelling pages. Here we present our work completed throughout the 2010 summer, the methodology behind our various models, and some of the conclusions we drew from those pieces of work.
Under the Hood
All our models are based upon a series of ordinary differential equations (ODEs) each of which have been derived from either prior research papers or our own research. These equations are solved computationally via the forth order Runge-Kutta method - the classical iterative method of approximating numerical ODEs. Seeking full control of the implementation of our model we decided against the use of mathematical packages and instead decided upon using a full fledged programming language to develop our models. Initially we decided upon GNU R, a programming language and environment for statistical computing. While R allowed for the rapid development of our initial models it was found that R lacked the fine grain control and the raw machine efficiency that we so required. A key problem that we encountered was that the majority of ODE solver libraries available for R were not in fact written in R, instead they were written in FORTRAN and C and the R component of the library meerly passed data to and from the external program. This was problematic as it did not allow us to access and modify the ODE solving algorithm which, in order to acquire the full set of data pertinent to any of or models and thus made future use of R infeasible. Instead we turned to C++, a far lower level language than R hoping for greater power of design. Being a compiled language (with a efficient compiler) C++ programs proved far faster than their R counterparts and offered a far finer degree of control. Initially we developed our own RK4 based ODE solver and put to work developing all our models as C++ programs. Output of the each of the models was processed and graphed using the gnuplot graphing utility. The first step in developing a usable model of the behaviour of the bistable switch was to manufacture a working model of the LuxR quorum sensing circuit (See our animation for an overview of how the circuit works). Through discussions with the biologists, we were able to generate a circuit diagram which allowed us to better visualise the workings of the system and split it up into individual reactions which we could then assign differential equations to. Ongoing testing of the model, in conjunction with further insights into the biology led to tweaking and adjustments, leading to further models with added degrees of complexity and greater realism. Our ultimate goal is to create a model accurately predicting the results of adding samples of our engineered E.coli into the human gut in the event of a cholera infection.
What we used
In line with the nature of iGEM all of the software used in development of our models was Free software. We wish to thank each of the following communities for producing such high quality software:
- [http://gcc.gnu.org/ GCC]
- [http://www.vim.org vim]
- [http://www.gnuplot.info gnuplot]
- [http://www.codeblocks.org/ Code::Blocks]
License
Similarly, in a continuing commitment to Free Software, all of our models are released under the [http://www.gnu.org/licenses/gpl.html GNU General Public License Version 3]. If you would like to view the code for our software it is available in the downloads page.
Components
Our project can be divided into two main components: the engineering of a bistable switch into the LuxR quorum sensing system, and the integration of CqsA (the biosynthetic enzyme present in the cholera system) into the LuxR circuit. The aim of the modeling side of the project was to treat these two tasks independently and on their completion construct a combined model. However, this initial aim was proved to be almost impossible due to the lack of rate constants for the cholera system, which has only been understood in its full complexity relatively recently [1]. In order to reach a compromise, we have built a number of qualitatively accurate models for the bistable LuxR system, and outlined a framework of differential equations for the cholera system which are correct at the time of writing, and which requires more rate constants to be of further use. The work done on the bistable switch included an investigation into why exactly such a configuration of genes exhibits hysteretic behavior, and what parameters are of importance in determining the “level” of bistability of the system.
The LuxR System
The LuxR quorum sensing system is common among the vibrio family, and the lux system of the luminescent bacterium V. Fischeri has been studied in great detail. This gave us a plentiful supply of scientific papers and review articles on which to base our understanding of the system. The LuxR system is underpinned by three quorum sensing molecules, those being the signalling molecule HSL; the HSL synthase LuxI and the transcriptional regulator LuxR. HSL may be generated in the cell by two means, either diffusion through the cell membrane from the external environment or being produced within the cell. Throughout the development of our models we considered a number of ways of trying to replicate this, and the details of these differenent techniques can be found in further sections. Whilst in the cell it may bind to LuxR, and two HSL molecules form a tetramer with two complementary LuxR molecules to form a complex which can then activate the lux operon. In the wild-type, this operon contains the genes coding for LuxI and those ultimately responsible for GFP production, with the luxR gene being located upstream and being constitutively produced. However, in our re-engineered operon the luxR gene lies downstream of the lux operon, thus its expression is also promoted. Hence once the promoter is activated, there is an increased production of LuxI, LuxR and also of GFP, which can therefore be used as an indicator of the promoter activity within the cell. Once transcription has been completed, the LuxI catalyses the production of more HSL from resources within the cell (which we have assumed exist in a sufficiently high concentration that they can be considered infinite). This may leave the cell due to a concentration gradient if the cell density in the medium is low, or otherwise will be used again in the loop, causing a positive feedback effect which will cause a high increase in the concentration of HSL. In this way the single bacterium can communicate with those surrounding it in order to evaluate whether it exists in sufficient numbers to overcome the immune system.
Differential Equations
In order to capture this behaviour mathematically, we developed a system of 8 differential equations which together encapsulate the main behaviour of the LuxR circuit. Each equation represents the change in concentration of either a molecule or piece of mRNA with time, and all are first order.
Eqn. 1: The HSL-LuxR complex is broken apart when either HSL or LuxR degrades, or it may naturally dissociate at a rate kDissHSLLuxR. It is prodcued by the association of HSL and LuxR at a rate kAssHSLLuxR.
Eqn. 3: The production of LuxRmRNA is promoted by the HSL-LuxR complex. We model this behaviour using a Hill function controlled by the parameters kMaxProductionRNA and kHalfMaxProductionRNA.
Eqn. 5 : LuxI is translated from the mRNA at a reate kTranslation and degrades at a rate kDegRNA
Eqn. 6: LuxR is translated from its mRNA at a constant rate, kTranslation. It can also increase due to the dissociation of the HSL-LuxR complex or the degradation of the HSL or LuxR within the complex, which will result in those molecules which didn't degrade being included in the concentration present in the cell.
Eqn. 7: The GFP concentration is our primary indicator of activation of the quorum circuit. Similarly to LuxI it is produced from its respective mRNA at the rate kTranslation and degrades at a rate kDegGFP.
The above equations form the backbone of our model and are the framework on which all of our further work is based.
Our next issue was then to develop a method of simulating a change from low to high cell density in order to see if our model displayed the bistability that was theoreticaly predicted.
The Models
Over the course of the project, our model has evolved through various stages of operability and complexity. These can be split into four key stages of development, the culmination of which being our finalised model of the LuxR quorum sensing network. Each model has its own set of assumptions and theoretical foundation which was either reaffirmed or dispelled as our understanding of the biology behind the system became more complete. However we present our methodology and our results for all of our models in order to allow the interested party to better understand the reasoning behind our work and follow the logic that brought us to our final conclusions.
The four models are labelled:
Model 2: Single Cell With Loop
Model 3: Psuedo Multi Cell One Dimension
Model 4: Psuedo Multi Cell Two Dimensions
Parameters
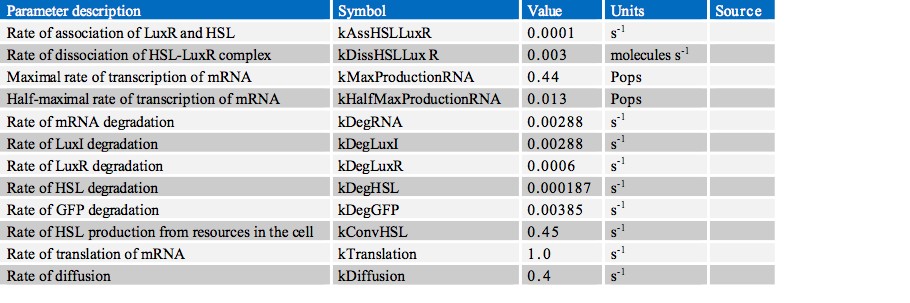
In finding the parameters for our model we searched through a great number of scientific papers in order to collate the various pieces of data which we required. Ultimately however, the most useful resource in our search proved to be the previous work done by other iGEM teams, notably Aberdeen’s Pico Plumber project of 2009. A comprehensive list of all rate constants used is given in the table below:
References
[1] Goryachev, A.B., D.J. Toh and T. Lee. “System analysis of a quorum sensing network: Design constraints imposed by the functional requirements, network topology and kinetic constant.” BioSystems 2006 83, 178-187
[2] Aberdeen 2009, "Parameters" iGEM wiki, <https://2009.igem.org/Team:Aberdeen_Scotland/parameters>
[3] Alon, Uri. “An Introduction to Systems Biology Design Principles of Biological Circiuts.” London: Chapman & Hall/CRC, 2007
[4] Subhayu Basu; “A synthetic multicellular system for programmed pattern formation.” Nature April 2005: 434, 1130-1134
[5]
 "
"