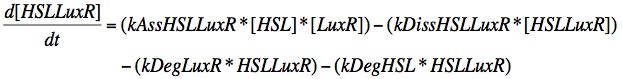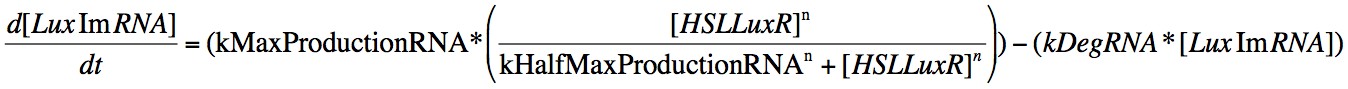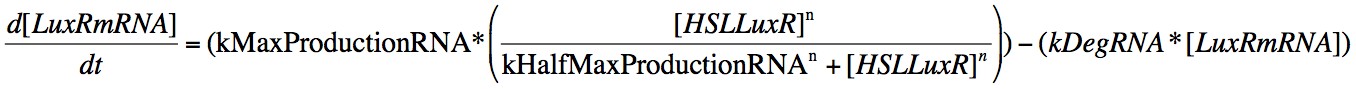Team:St Andrews/project/modelling
Modelling
Contents |
Introduction
Hello and welcome to the St. Andrews iGEM 2010 modelling pages. Here we present our work completed throughout the 2010/2011 summer, the methodology behind our various models, and some of the conclusions we drew from those pieces of work.
Under the Hood
All our models are based upon a series of ordinary differential equations (ODEs) each of which have been derived from either prior research papers or our own research. These equations are solved computationally via the forth order Runge-Kutta method - the classical iterative method of approximating numerical ODEs. Seeking full control of the implementation of our model we decided against the use of mathematical packages and instead decided upon using a full fledged programming language to develop our models. Initially we decided upon GNU R, a programming language and environment for statistical computing. While R allowed for the rapid development of our initial models it was found that R lacked the fine grain control and the raw machine efficiency that we so required. A key problem that we encountered was that the majority of ODE solver libraries available for R were not in fact written in R, instead they were written in FORTRAN and C and the R component of the library meerly passed data to and from the external program. This was problematic as it did not allow us to access and modify the ODE solving algorithm which, in order to acquire the full set of data pertinent to any of or models and thus made future use of R infeasible. Instead we turned to C++, a far lower level language than R hoping for greater power of design. Being a compiled language (with a efficient compiler) C++ programs proved far faster than their R counterparts and offered a far finer degree of control. Initially we developed our own RK4 based ODE solver and put to work developing all our models as C++ programs. Output of the each of the models was processed and graphed using the gnuplot graphing utility. The first step in developing a usable model of the behaviour of the bistable switch was to manufacture a working model of the LuxR quorum sensing circuit (See our animation for an overview of how the circuit works). Through discussions with the biologists, we were able to generate a circuit diagram which allowed us to better visualise the workings of the system and split it up into individual reactions which we could then assign differential equations to. Ongoing testing of the model, in conjunction with further insights into the biology led to tweaking and adjustments, leading to further models with added degrees of complexity and greater realism. Our ultimate goal is to create a model accurately predicting the results of adding samples of our engineered E.coli into the human gut in the event of a cholera infection.
What we used
In line with the nature of iGEM all of the software used in development of our models was Free software. We wish to thank each of the following communities for producing such high quality software:
- [http://gcc.gnu.org/ GCC]
- [http://www.vim.org vim]
- [http://www.gnuplot.info gnuplot]
- [http://www.codeblocks.org/ Code::Blocks]
License
Similarly, in a continuing commitment to Free Software, all of our models are released under the [http://www.gnu.org/licenses/gpl.html GNU General Public License Version 3].
Components
Our project can be divided into two main components: the engineering of a bistable switch into the LuxR quorum sensing system, and the integration of CqsA (the biosynthetic enzyme present in the cholera system) into the LuxR circuit. The aim of the modeling side of the project was to treat these two tasks independently and on their completion construct a combined model. However, this initial aim was proved to be almost impossible due to the lack of rate constants for the cholera system, which has only been understood in its full complexity relatively recently [1]. In order to reach a compromise, we have built a number of qualitatively accurate models for the bistable LuxR system, and outlined a framework of differential equations for the cholera system which are correct at the time of writing, and which requires more rate constants to be of further use. The work done on the bistable switch included an investigation into why exactly such a configuration of genes exhibits hysteretic behavior, and what parameters are of importance in determining the “level” of bistability of the system.
The LuxR System
The LuxR quorum sensing system is common among the vibrio family, and the lux system of the luminescent bacterium V. Fischeri has been studied in great detail. This gave us a plentiful supply of scientific papers and review articles on which to base our understanding of the system. The LuxR system is underpinned by three quorum sensing molecules, those being the signalling molecule HSL; the HSL synthase LuxI and the transcriptional regulator LuxR. HSL may be generated in the cell by two means, either diffusion through the cell membrane from the external environment or being produced within the cell. Throughout the development of our models we considered a number of ways of trying to replicate this, and the details of these differenent techniques can be found in further sections. Whilst in the cell it may bind to LuxR, and two HSL molecules form a tetramer with two complementary LuxR molecules to form a complex which can then activate the lux operon. In the wild-type, this operon contains the genes coding for LuxI and those ultimately responsible for GFP production, with the luxR gene being located upstream and being constitutively produced. However, in our re-engineered operon the luxR gene lies downstream of the lux operon, thus its expression is also promoted. Hence once the promoter is activated, there is an increased production of LuxI, LuxR and also of GFP, which can therefore be used as an indicator of the promoter activity within the cell. Once transcription has been completed, the LuxI catalyses the production of more HSL from resources within the cell (which we have assumed exist in a sufficiently high concentration that they can be considered infinite). This may leave the cell due to a concentration gradient if the cell density in the medium is low, or otherwise will be used again in the loop, causing a positive feedback effect which will cause a high increase in the concentration of HSL. In this way the single bacterium can communicate with those surrounding it in order to evaluate whether it exists in sufficient numbers to overcome the immune system.
Differential Equations
In order to capture this behaviour mathematically, we developed a system of 8 differential equations which together encapsulate the main behaviour of the LuxR circuit. Each equation represents the change in concentration of either a molecule or piece of mRNA with time, and all are first order.
Eqn. 2: The HSL-LuxR complex is broken apart when either HSL or LuxR degrades, or it may naturally dissociate at a rate kDissHSLLuxR. It is prodcued by the association of HSL and LuxR at a rate kAssHSLLuxR.
Eqn. 3: The production of LuxRmRNA is promoted by the HSL-LuxR complex. We model this behaviour using a Hill function controlled by the parameters kMaxProductionRNA and kHalfMaxProductionRNA.
Eqn. 6 : LuxI is translated from the mRNA at a reate kTranslation and degrades at a rate kDegRNA
Eqn. 7: LuxR is translated from its mRNA at a constant rate, kTranslation. It can also increase due to the dissociation of the HSL-LuxR complex or the degradation of the HSL or LuxR within the complex, which will result in those molecules which didn't degrade being included in the concentration present in the cell.
Eqn. 8: The GFP concentration is our primary indicator of activation of the quorum circuit. Similarly to LuxI it is produced from its respective mRNA at the rate kTranslation and degrades at a rate kDegGFP.
The above equations form the backbone of our model and are the framework on which all of our further work is based.
Our next issue was then to develop a method of simulating a change from low to high cell density in order to see if our model displayed the bistability that was theoreticaly predicted.
The Models
Method 1: No feedback loop
The first method we attempted was to put the user in control of the change in HSL within the cell, and take any HSL produced and remove it from the system entirely. In this fashion a gradual increase in cell density was simulated by a linear “ramp up” of the HSL in the cell; a gradual decrease (presumably due to cell death) was simulated by a linear “ramp down” in HSL. The activation of the cell was measured by plotting the GFP concentration.
Method 2: Feedback loop
Our second model introduced the concept of an external environment into which the HSL could diffuse into. This was assumed to be of infinite volume and thus the concentration of HSL in this region would always be zero, regardless of the quantity of HSL leaving the cell. In order to implement this modification we produced a new differential to desrcibe the change in HSL. (display equation).
The creation of HSL is dictated by kConv, which is associated with the ability of LuxI to catalyse the conversion of resources into HSL. The concentration is reduced by the association with LuxR and by natural degredation. It is also affected by the degredation of molecules in the HSL-LuxR complex in the same way that LuxR is. We also introduce a diffusion term which accounts for HSL diffusing out of the cell due to a concentration gradient between the cell and the external environment.
Method 3: Cell Growth and death
The results produced from both of our previous models were unsatisfactory, since neither gave us quantifiable data from which experimental comparisons could be made, although the switching on was clearly visible in both. Therefore it was decided that in order to properly capture the mechanism of bistability it was essential to have some element of cell number, and as such we must simulate the growth of a cell colony rather than artificially increase the amount of HSL in our external environment. Several crucial elements were added to the model to incorporate this new outlook:
i. A new variable 'Number of cells' was added
ii. Two new functions which simulate cell growth and cell death
iii. A new paramter 'Volume'
The number of cells is set at the beginning of the simulation by the user. Based on a doubling time of 20 minutes, the variable is increased every increment by the cell growth function. In order to simulate the increase in HSL due to these new cells, each new cell is accompanied by an increase in HSL which is equal to that being contributed by the cells already present in the system. (VOLUME THING IN DIFFERENTIALS). Similarly we included a cell death function which decreases the number of cells at a halving rate of 20 minutes in tandem to the growth rate.
Parameters
In finding the parameters for our model we searched through a great number of scientific papers in order to collate the various pieces of data which we required. Ultimately however, the most useful resource in our search proved to be the previous work done by other iGEM teams, notably Aberdeen’s Pico Plumber project of 2009. A comprehensive list of all rate constants used is given in the table below.
Results
Model 1
In order to simulate the effect of the cell colony growing in number we first set the change in HSL concentration to a fixed value and ran the model until a steady state was reached. It can be clearly seen from figure . that the level of GFP in the cell reaches a point where the concentration starts to sharply increase before a plateau is reached and there is no further activity. This is the switch-on, where the cell has moved from a down-regulated to an up-regulated state and starts to produce greater amounts of HSL, LuxR, LuxI and GFP.
The final values of all the molecules are RNAs are then substituted into the model as the initial values for the next run and the HSL is reduced at a fixed rate, producing the data shown in figure . It can be seen that the up-regulation is maintained for a much lower HSL threshold than when the first run. In fact, the cell never fully returns to a down-regulated state again. After trying to achieve this through decreasing the rate at which the HSL is taken away and increasing the number of increments for which the model is run, it was decided that our model simply did not produce the behaviour we were looking for. Figure shows how the concentrations of the various molecules and the mRNAs changes over the transition from down- to up-regulated states. The model predicts low concentrations of the HSL-LuxR complex which is theoretically predicted, but in general the results were unsatisfactory as to drawing any real conclusions about the causes or otherwise of the bistability.
Model 2
The switching on behaviour produced by this model is shown in figure . This switching on can be interpreted as the cell turning itself on due to the HSL it produces not diffusing out of the cell at a high enough rate. Therefore there is a considerable concentration of HSL remaining in the cell to maintain the feedback loop and produce more HSL. Thus regardless of the initial concentrations our cell always switches on. This does not match with the true biological scenario at all. Quorum sensing is designed such that cells will only become up-regulated when present at a certain critical cell density. Therefore the suggestion made by our results that a single cell can self-activate undermines this principle entirely.
Model 3
On running the model through the cell growth, stationary and cell death phases, the first example of ‘true bistability’ is produced, see figure . Since this model contains spatial dimensions we are able to determine a specific cell density at which the switch happens, and this is comparable to the value predicted by other models and by experimental evidence. There is also a clear difference between the switch-on and switch-off thresholds which we hypothesise is caused by…
 "
"