From 2010.igem.org

Revision as of 09:32, 21 October 2010 by Anita (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

Department of Bioengineering

Division of Molecular Biosciences

Temporary sub-menu:

Objectives; Detailed Description; Parameters & Constants; Results & Conclusion;Download MatLab Files;

Output Amplification Model

Detailed Description

1. Model based on Law of Mass Action

During a meeting with our advisors, it was noted that our initial models (which had assumed that our system obeyed Michaelis-Menten kinetics) were wrong as the assumptions made by Michaelis-Menten approximation were not obeyed by our system. Click on the button below to learn more about our models based on Michaelis-Menten kinetics.

Abandoned Initial Attempts

Model based on Michaelis Menten Kinetics

HIV1

File:Slide2.JPG At each stage of amplification a distinct protease is being used	Equations <math>\dot{m}=k_{to} - d_{to}m\,\!</math> <math>\dot{p_h} = k_hm - d_hp_h</math> <math>\dot{p_t} = k_tp_h - d_tp_t</math> <math>\dot{p_g} = k_gp_t - d_gp_g</math>	Parameters <math>k_{to}\mbox{...transcription rate of HIV1}</math> <math>d_{to}\mbox{...degradation rate of mRNA coding for HIV1}</math> <math>k_h\mbox{...translation rate of HIV1}</math> <math>d_h\mbox{...degradation rate of HIV1}</math> <math>k_t\mbox{...production rate of TEV by HIV1}</math> <math>d_t\mbox{...degradation rate of TEV}</math> <math>k_g\mbox{...production rate of GFP by TEB}</math> <math>d_g\mbox{...degradation rate of GFP}</math>

TEV

File:TEV.jpg TEV is used at both stages of amplification	Equations <math>\dot{m} = k_{to} - d_{to}m</math> <math>\dot{p_t} = k_tm - d_tp_t</math> <math>\dot{p_{ts}} = k_{ts}p_t - d_{ts}p_{ts}</math> <math>\dot{p_g} = k_{g1}p_t + k_{g2}p_{ts} - d_gp_g</math>	Parameters <math>k_{to}\mbox{...rate of transcription by TEV}</math> <math>d_{to}\mbox{...degradation rate of mRNA coding for TEV}</math> <math>k_t\mbox{...rate of translation of TEV}</math> <math>d_t\mbox{...degradation rate of TEV}</math> <math>k_{ts}\mbox{...rate of production (fusion) of split TEV}</math> <math>d_{ts}\mbox{...degradation rate of split TEV}</math> <math>k_{g1}\mbox{...rate of production of GFP by full TEV}</math> <math>k_{g2}\mbox{...rate of production of GFP by split TEV}</math> <math>d_g\mbox{...degradation rate of GFP}</math>

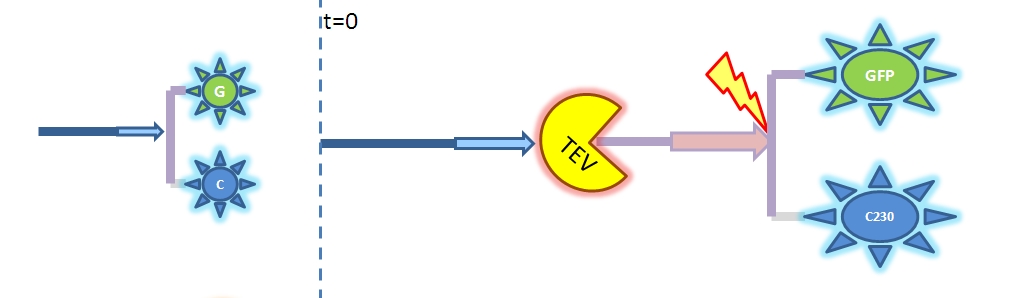
Improved Model which accounts for enzyme reactions

TEV

File:TEV.jpg TEV is used at both stages of amplification	Equations 1. Production of TEV from transcription <math>\dot{p_t} = s_t - d_tp_t</math> <math>s_t = \dfrac{k_tk_{to}}{d_{to}}</math> 2. Production of split TEV from transcription <math>\dot{p_{st}} = s_{st} - d_{st}p_{st}</math> 3. Production of split GFP from transcription <math>\dot{p_{sg}} = s_{sg} - d_{sg}p_{sg}</math> 4. Production of fused split TEV catalysed by TEV (1) <math>\dot{p_{ts}} = \dfrac{V_{max,t}[p_{st}]}{K_{m,ts} + [p_{st}]} - d_{ts}p_{ts}</math> 5. Production of GFP catalysed by TEV (1) and fused split TEV (4) <math>\dot{p_g} = \dfrac{V_{max,tg}[p_{sg}]}{K_{m,tg} + [p_{sg}]} + \dfrac{V_{max,tsg}[p_{sg}]}{K_{m,tsg} + [p_{sg}]} - d_gp_g</math>

Implementation in Matlab
The Matlab code for the different stages of amplification and diagrams can be found [http://www.openwetware.org/wiki/Image:Modelling.docx here].

Kinetic constants

Constants for the Protein Display Model

	GFP	split GFP	TEV	split TEV
K_m and k_cat	-	K_m = 0.061; k_cat = 0.16; [1]	40% of value for TEV	-
Half-life or degradation rate	Half-life in B.sub approximately 1.5 hours	-	-	Half-life shorter than GFP
Production rate in B.sub	-	-	-	-

Conclusion

We were not able to obtain all the necessary constants. Hence, we decided to make educated guesses about possible relative values between the constants as well as varying them and observing the change in output.

As the result, we concluded that the amplification happens at each amplification level proposed. The magnitude of amplification varies depending on the constants. There is not much difference between using TEV or HIV1.

References

Kapust R. et al (2001) Tobacco etch virus protease: mechanism of autolysis and rational design of stable mutants with wild-type catalytic proficiency. Protein Engineering. [Online] 14(12), 993-1000. Available from: http://peds.oxfordjournals.org/cgi/reprint/14/12/993 [Accessed 28th July 2010]

In order to be able to use Michaelis Menten kinetics, there a lot of assumptions that have to be made. A few of these assumptions were not met by our system:

Vmax is proportional to the overall concentration of the enzyme.

Since we are continuously producing enzyme, Vmax will change. Therefore the conservation E₀ = E + E_S does not hold for our system.

Substrate >> Enzyme

We are producing both substrate and enzyme, so we have approximately the same amount of substrate and enzyme.

Enzyme affinity to the substrate has to be high.

Therefore, the model above is not representative of the enzymatic reaction. As we cannot use the Michaelis-Menten model we will have to solve from first principle (which involves writing down all of the biochemical equations and solving for these in Matlab).

Change of output

During our literature research, we came across a better output, so we abandoned the idea of using GFP as an output. Instead, we are using catechol. An enzyme, dioxygenase, will be acting on the catechol, which will then result in a coloured output. Catechol will be added to the bacteria manually (i.e. the bacteria will not produce catechol). Hence, in our models dioxygenase will be treated as an output as this enzyme is the only activator of catechol in our system. This means that the change of catechol into its colourful form is dependent on the dioxygenase concentration.

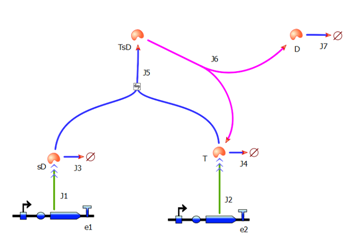
2. Model preA: Simple production of dioxygenase

Transcription and translation
(simple production) of dioxygenase.

This model includes transcription and translation of the dioxygenase. It does not involve any amplification steps. It is our control model against which we will be comparing the results of other models.

3. Model A: Activation of Dioxygenase by TEV enzyme

1-step amplification.

This model consists of the basic enzymatic reaction:

Equations showing enzymatic reaction between TEV and split Dioxygenase

This is a simple enzymatic reaction, where TEV is the enzyme, Dioxygenase the product and split Dioxygenase the substrate. Choosing k₁, k₂, k₃ as reaction constants, the reaction can be rewritten in these four sub-equations:

PDEs describing the reaction presented above

These four equations were implemented in Matlab, using a built-in function (ode45) which solves ordinary differential equations.

Implementation in TinkerCell

Another approach to model the amplification module would be to implement it in a program such as TinkerCell (or CellDesigner). This would be useful to check whether the Matlab model works.

Model A implemented in TinkerCell.

4. Model B: Activation of Dioxygenase by TEV or activated split TEV enzyme

2-step amplification.

This version includes the following features:

2 amplification steps (TEV and split TEV)
Split TEV is specified to have a and b parts
TEVa is forbidden to interact with TEVa (though in reality there could be some affinity between the two). Same for the interaction between Tevb and Tevb
Both TEV and TEVs are allowed to activate dioxygenase
Dioxygenase is assumed to be active as a monomer
Activate split TEV (TEVs) is not allowed to activate sTEVa or sTEVb (this kind of interaction is accounted for in the next model version)
This model does not include any specific terms for time delays

5. Model C: Further improvements

This model has not been implemented because of the conclusions that we reached from Models A and B. It would include the following features:

activated split TEV (TEVs) is allowed to activate not only sD but sTEVa and sTEVb

Team:Imperial College London/Modelling/Output/Detailed Description