Team:SDU-Denmark/project-m
From 2010.igem.org
Physical Modelling
Motivation
One of the main ideas in the project is to control the flow induced by a bacterial coating inside a micro-tube. What we want to do in this part of the project is to study the mechanics of such a system, and how different parameters will affect it. One way to do this is to create a physical model that describes the most essential features of the system. Our work connected to the development of such a model is presented in the following. The basis for any model is an understanding of the physical system in question, therefore we will start with a short review of the hydrodynamic properties of flagella and the bacterial pumping system constructed by M. J. Kim and K. S. Breuer [1].
The real system
The "real" system that we want to model is a bacterial pump as described by M. J. Kim and K. S. Breuer [1]. This is in principle just a microscopic chamber with a flow channel 15µm deep, 200µm wide and 15mm long, covered on the inside by a layer of flagellated bacteria. The bacterial layer described by M. J. Kim and K. S. Breuer [1] is very dense and uniform, with a spacing between each bacterium of less that 1µm and 80% of the bacteria adhered to the surface as single bacteria. To get a better understanding of the origin of the flow created from the bacterial coating, it is important to understand the structure of the bacterial flagellum.
The bacterial flagellum consists of 3 major parts, a rotary motor complex, a hook and a filament. The first part creates the rotary motion of the flagellum and the second part serves as a flexible coupling between the torque creating part and the filament. For our model the filament is the most interesting part. This is responsible for the conversion of the rotary motion into a linear thrust. The filament is a self-assembling polymeric structure composed of flagellin protein subunits. These are arranged in a circular way to create a hollow helical structure, with a typical width of 120-250Å and a length of 10-15µm [2]. A bacterium as E. coli typically has around 10 flagella [3]. These filaments are able to adopt a wide range of conformations under the induced torque. Numeric studies [4-5] and empiric results [6] suggest that the conformation is strongly dependent on the hydrodynamic environment that surrounds the flagellum and its rotational direction. When several flagella rotates counterclockwise the flagella tends to bundle together in a single helix structure, due to the hydrodynamic interactions [4]. A phosphorylationcascade causes the flagella to turn clockwise at irregular intervals. This induces a sequence of deformations that changes the single helix structure of the flagella and unravels the bundle. This is known as tumble mode.
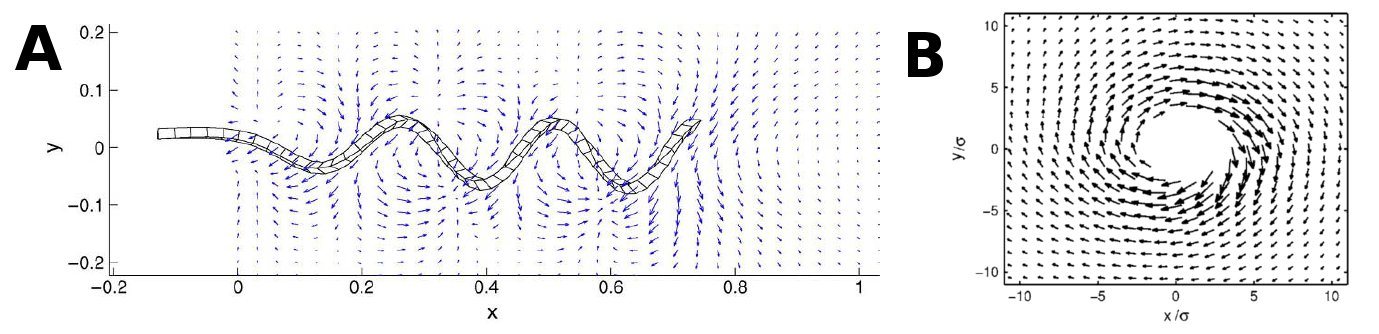
To be able to model the flow created by a bacterial coating of a tube it is essential to know what kind of flowfield a single flagellum/bundle will create. This has primarily been investigated by numerical approaches, where the flagella are modelled as semiflexible hookian systems. Several studies [4-5] suggests that the flow created from a single flagellum is highly non-uniform, but to some degree circular symmetric at the end of the flagellum (see figure 2 A and B, below). When the flagella bundle together Floresa, H. et al. [4] suggests that this symmetry becomes less clear and flow becomes even more complicated.
All these results refer to flagella moving freely in aqueous solution, the question is now, whether the same is true for bacteria stricking to the surface of a narrow tube? Turner, L. et al. [6] suggests that bacteria completely fixed to a surface will deviate from the bundel behavior, but it is unclear what happens if the fixation is more partial or if the bacteria are surrounded by a flow. To summarize we have to model a very dense system of elongated objects that each give rise to an unsymmetrical flow, which depends self-consistent of the total flow and gives rise to self-organization. This is indeed not a simple task, and quite a few simplifying assumptions have to be made. These will be startingpoint of the next part.
Description of model
A flagellum creates propulsion by spinning around in a helical shape. Since the flagella/flagellabundles, take on a helical shape, the most accurate thing to do would be to model them as such, but doing this would become quite advanced for even one flagellum, not to mention an entire system. Since we are limited in both time and computerpower, we will have to simplify the system a bit. One thing we can do is to consider all the flagella of a bacterium to form one bundle, even though doing so for a bacterium stuck to a wall is questionable. The overall result of this spinning bundle is that the flow moves in an almost straight line. This could be modelled as a pointforce on the tip of the flagellabundle pointing in the same direction as the bundle. The size of this force can be approximated by calculating the drag on a swimming bacterium. If the bacterium is considered almost spherical the drag force can be calculated by using the formula for Stokes flow past a sphere:
where η (=8.94•10-4 Pa•s for water) is the viscosity of the fluid in which the bacterium is swimming, r (=0.4•10-6 m) is the radius of the bacterium and v (=50•10-6 m/s) is the velocity of the swimming bacterium.
The dragforce and thereby the force created by the flagellabundle of one E. coli is
The system we are trying to model consists of a lot of bacteria stuck to a wall, but the part we are interested in is the flagellae and the forces they create. We therefore ignore the bodies of the bacteria, and instead consider the flagella as being stuck directly to the wall, with one end glued to the wall and the other pointing out into the fluid.
Next step is to figure out what kind of flowfield, such a pointforce creates. The flowfield created by a pointforce in a fluid with no walls or other obstructions near it can be calculated using the corresponding Green's function known as the stokeslet:
where the three indices on G represent the number of walls and their matrix-coordinates, h is the distance between the pointforce and the wall and r is the vector from the pointforce to where the flow is to be calculated.
If the pointforce is placed near a wall, modifications must be made since the flow velocity has to go to zero at the boundary (known as the no-slip condition). This is done by using the Oseen-Blake tensor. Simply described, the Oseen-Blake tensor creates a mirror image of our force on the other side of the wall, thus cancelling the flow near the wall (This is not a completely accurate description, but rather an intuitive one).
In our case the flagella are stuck to a wall, so we use the Oseen-Blake tensor.
Here R is the vector from the mirrorpoint of the force to the point where the flow is to be calculated.
The two formulas above are based on [8].
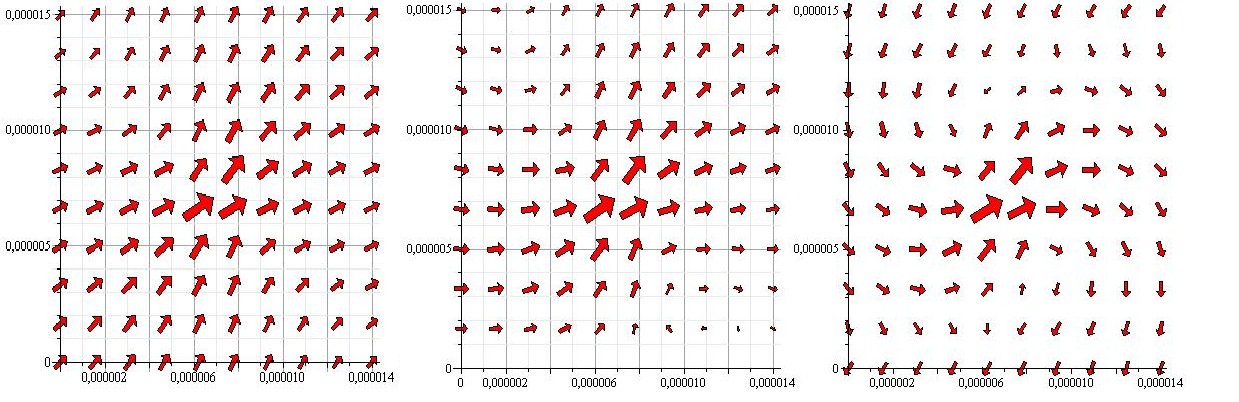
In our case the system we are trying to describe is a microtube. This means that the width of the tube is so small, that the forces created by the flagella are not only close to the wall to which the bacteria are stuck, but also close to the opposite wall. This presents an interesting problem. Since the Oseen-Blake tensor works by creating a mirrorpoint of the real force on the opposite side of the wall, we will need a mirrorpoint behind the other wall if we are to uphold the no-slip condition. But the mirror forces also affect the flow near the other wall. In order to cancel this effect one could create another mirrorforce, corresponding to each of the mirror forces, but of course these would obstruct each other to, requirering yet more mirror forces. In the end we decided to see how precise the system would be for one mirrorpoint behind each wall. This corresponds to taking the equation above and adding the three last terms once more, but with the mirrorvector corresponding to the other wall.
The flowfield corresponding to this is shown below.
As the above figures show, there is quite a difference depending on how many walls you take in to consideration. We decided to keep working with both the single-wall and the double-wall flowfields.
Flagella dynamics
The next thing to be considered was how the flagella depends on the fluid flow, i.e. if we place a bacterium at an angle θ with the wall will it remain at that angle or will it get pulled around by the flow in the tube, thus changing its position. The two extreme situations would be either that the flagella stick very hard to the surface and are therefore unaffected by the flow or that they stick very gently to the surface and that their angle depends completely on the flow. In order to create an intermediate situation, we could constrain each flagellum with a harmonic potential, pulling it toward a favored angle (connected to the initial orientation of the fagella when it stick to the surface). We believe the answer lies somewhere in between the two extremes, but that does not mean the extremes can't tell us anything. We therefore decided to create a model in which the flagella keeps still, and one where they are affected by the flow and a potential. The size of the potential can always be set to zero if we want to study the flagella without an affecting potential.
The basic idea then is that every flagella stuck to the surface creates their own flowfields. To get the entire flowfield we add together all the flowfields created by the individual flagella. In the case where the flagella are stationary the assumptions made so far actually shows the system. For flagella that are able to move it's a bit more tricky.
The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the spheres. An image, showing some of the vectors involved and the procedure we used is shown below.
First the fluid velocity at the given point is found. The method is the same whether there is 0, 1 or two walls, but the tensor used varies.
The dragforce created by the fluid on the bead is calculated using the same formula we used in chapter 3
Once we have the force we can use it to calculate the torque on the bead, we then summarize the torques of the individual beads to get the total torque
We then go to from the torque to the angular acceleration by dividing with the inertia. This is also where we introduce the potential, that we mentioned earlier
Now that we have the angular acceleration we can insert it into the equation of motion. This allows us to calculate the position of the flagella at the next timestep by using it's position at the current and at the previous timestep.
In the end this model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after that the two velocity never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of computerpower we decided that instead of force calculations we would simpy find the flowvelocity at the tip of the flagellum and convert that directly to the angular velocity of the flagellum.
A 2-D model of the system
In this chapter we will present our model a bit more precisely and present some of the results it has given us. The 2-D model consists of a one dimensional grid, to which flagella are attached. Each flagellum produces a force which creates a flow which pushes every other flagellum, and thus a dynamic system is created. To calculate how big the flow will be at a given point, a vector from the tip of the force-producing flagellum to the point where you wish to know the flow must be created. To know how a flagellum is affected by the flow, the flow at the tip of the flagellum must be calculated. Once you have this vector and the vector corresponding to the force. The flow can be calculated using stokeslet or the Oseen-Blake tensor, depending on whether there is a wall nearby. In our system there is a wall so we will be using the Oseen-Blake tensor. This means that we are also required to find a vector from the mirrorpoint of the force, to the point at which we wish to know the flow. After this it is a matter of summarizing over all the flagella to find the total flowfield. The situation (disregarding the mirrorpoint) is sketched in figure XX. The completely velocity controlled equation of motion then becomes(using the notation in figure XX): The best way to illustrate the result from this model is to see it in action, so here follows the time series of a system af size 20 (only the 4 flagella in the middel of the system is shown), where the elastic constant is zero:
It is clear that the flagella tends to lie down and stabilize in an almost flat position in this case. In the following figure we have made a lot of these runs, but with varying average start-angle
As the figure shows a very small deviation in the starting angle will cause a much bigger deviation in the end. The flagella in the systems used in this graph all lied down, but to which side the flagella went was highly dependent on the start konfiguration. When the mean angle was zero corresponding to a vertical flagellum it was pretty much 50-50, but when the start angles were pushed a bit to one side it had a tendency to shift the entire system in that direction. This tells us that if you can control the starting angle, it will go a long way towards creating a uniform flow.
A stationary 2-D model
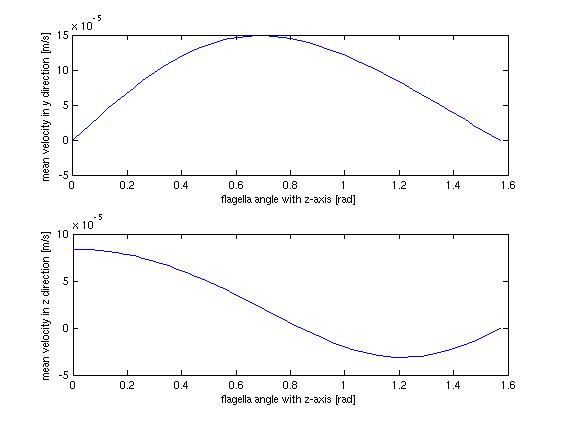
The stationary model, doesn't offer much when it comes to dynamics and interesting behavior, which shouldn't surprise anyone. It does however offer us the opportunity to investigate at which angle the flow in the direction of the tube is highest, which could be helpful when planning how to optimize the use of bacteria as a source of flow.
The above figure shows the average flow velocity as a function of the angle of the flagella. In the abov case only one wall is taken in to account. The one of most importance is the top-one which shows the flow velocity parallel to the tube. According to these figures we get the best velocity at an angle of around 0.7 rad or approximately 40 degrees, where the angle is measured from the axis perpendicular to the wall.
Model expansions
3-D
All programs we have written have been created for easy transfer from the 2-D model to a 3-D model. And we have made the adjustments needed in order for it to become 3-D, unfortunately we have not had time to check it for errors and to gain some results.
A flagella row on the other wall
In our model we settled for placing bacteria on one wall. During real-life application, flagella would most likely be placed on both walls. This is not something we have tried to implement in our model, though to do so should just be a matter of creating an extra grid an adapting the existing model a bit. If this was done it would go a long way towards improving the usability of the model
A better double-wall approximation
The double-wall approximation we made is a very rough approximation based on what you do when you have a single wall. The model could be improved alot by making a better approximation, though aside from simply creating more mirror-pints, we have not investigated how this could be done, but it would most likely be quite difficult.
References
1. Kim MJ, Breuer KS, [http://microfluidics.engin.brown.edu/Breuer_Papers/Journals/Small2008_Bacterial_Pump.pdf Microfluidic pump powered by self-organizing bacteria], Small 4, 111-118. (2007)
2. Berg HC, [http://www.annualreviews.org/eprint/cDJrS190m62mDRwHrlp9/full/10.1146/annurev.biochem.72.121801.161737 The rotary motor of bacterial flagella], Annu. Rev. Biochem. 72, 19-54. (2003)
3. Berg HC, E. coli in Motion, Springer, New York. (2004)
4. Floresa H, Lobatonb E, Méndez-Diezc S, Tlupovad S, Cortezd R, A study of bacterial flagellar bundling, Bulletin of Mathematical Biology 67 137–168. (2005)
5. Reicherta M, Stark H, Synchronization of rotating helices by hydrodynamic interactions, Eur. Phys. J. E 17, 493-500. (2005)
6. Turner L, Ryu WS, Berg HC, Real-Time Imaging of Fluorescent Flagellar Filaments, JOURNAL OF BACTERIOLOGY, 2793–2801. (2000)
7. http://commons.wikimedia.org/wiki/File:Flagellum_base_diagram.svg
8. Uchida N, Golestanian R, Synchronization and Collective Dynamics in A Carpet of Microfluidic Rotors. (2009)
We know what we expect from our system, but does the math agree?
Contents[hide] |
 "
"