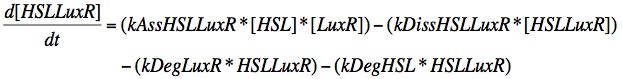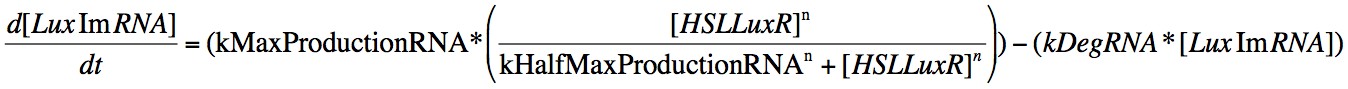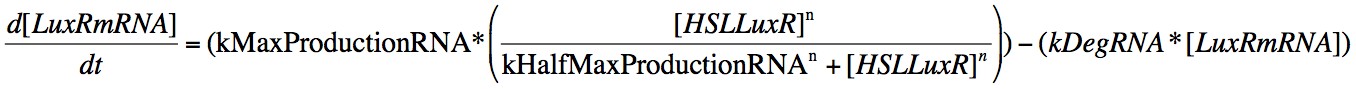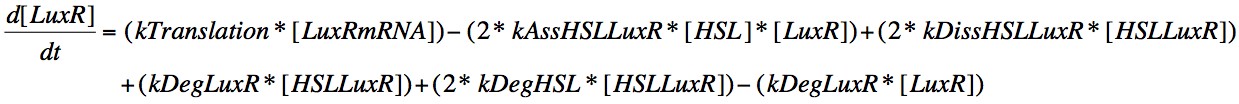Team:St Andrews/project/modelling/models/ODEs
Ordinary Differential Equations (ODEs)
Contents |
What is an ODE?
An ordinary differential equation (ODE) is a relation that contains functions of only one independent variable and one or more of their derivatives with respect to that variable. This is in contrast to a partial differential equation which can be defined, a relation involving an unknown function or functions of several independent variables and their partial derivatives with respect to those variables. Of course, in our work we are interested in how all the different components of our quorum sensing system change with time and so will use ODEs where the differentials are with respect to time (dt). Since we have a number of chemicals present at any one time in the system we require a differential equation to describe how each will change in time, thus we develop a system of interlocking ODEs which are all interconnected by shared variables.
Typical ODE elements
Since each chemical participates in different reactions and biological process, there will be great variation in the ODEs describing them. However there are several types of reaction which are common to most of the chemicals and these are discussed below
Natural degradation
Over time, the chemicals within a cell will degrade, whether this be due to use in other processes, being broken down by other chemicals, or simply breaking apart due to their natural instability. This results in a decrease in concentration over time and so is represented by a negative factor in our equations. The rate of degradation is proportional to the concentration of substance present and so in general the term is of the form:
Association
Two or more substances may come together and bind to create a new substance entirely. This process is know as association. The rate at which something associates will clearly be dependent not only upon the concentration of itself but of the other substances which it is associating with. Since a new substance is actually formed, association will be a positive contribution in some equations and negative in others. Typically it will be represented by the relationship:
Dissociation
The equations
In order to capture the behaviour behaviour mathematically, we developed a system of 8 differential equations which together encapsulate the main behaviour of the LuxR circuit. Each equation represents the change in concentration of either a molecule or piece of mRNA with time, and all are first order.
Eqn. 1: The HSL-LuxR complex is broken apart when either HSL or LuxR degrades, or it may naturally dissociate at a rate kDissHSLLuxR. It is prodcued by the association of HSL and LuxR at a rate kAssHSLLuxR.
Eqn. 3: The production of LuxRmRNA is promoted by the HSL-LuxR complex. We model this behaviour using a Hill function controlled by the parameters kMaxProductionRNA and kHalfMaxProductionRNA.
Eqn. 5 : LuxI is translated from the mRNA at a reate kTranslation and degrades at a rate kDegRNA
Eqn. 6: LuxR is translated from its mRNA at a constant rate, kTranslation. It can also increase due to the dissociation of the HSL-LuxR complex or the degradation of the HSL or LuxR within the complex, which will result in those molecules which didn't degrade being included in the concentration present in the cell.
Eqn. 7: The GFP concentration is our primary indicator of activation of the quorum circuit. Similarly to LuxI it is produced from its respective mRNA at the rate kTranslation and degrades at a rate kDegGFP.
The above equations form the backbone of our model and are the framework on which all of our further work is based.
Our next issue was then to develop a method of simulating a change from low to high cell density in order to see if our model displayed the bistability that was theoreticaly predicted.
 "
"