Modeling of binding site efficiency

shRNA binding sites

As the title of our project states, “DNA is not enough”. There are several upper-level regulation systems in superior organisms. Our main idea was using miRNA to tune down the expression of genes, having tissue-specific, exactly tuned gene therapy as objective.

miRNA are non-coding regulatory RNAs functioning as post-transcriptional gene silencers. After they are processed, they are usually 22 nucleotides long and they usually bind to the 3’UTR region of the mRNA (although they can also bind to the ORF or to the 5'UTR), forcing the mRNA into degradation or just repressing translation.

In vegetal organisms, miRNA usually bind to the mRNA with extensive complementarity. In animals, interactions are more inexact, creating a lot of uncertainty in the in silico prediction of targets.

The seed of the miRNA is usually defined as the region centered in the nucleotides 2-7 in the 5’ end of the miRNA, and it usually requires extensive pairing. (For the sake of simplicity, we extended slightly the term seed to include the nucleotides 1-8.)

Outside the seed, the existence of supplemental pairing (at least 3 contiguous nucleotides and centered in nucleotides 13-16 of the miRNA) stabilizes the bound complex and increases the efficacy of the binding site.

Binding sites with a high local AU density around the binding site have proven to be more effective (possibly because of the destabilization of the mRNA secondary structure around the site).

The position of the binding site not in the middle of the 3’UTR but either at the end or 15 nt after the stop codon increases the efficacy of repression. IS THE FOLLOWING REALLY NECESSARY? I DON'T THINK I CAN MANAGE TO EVER FIT THE TOPIC HERE... About the mechanistics of the repression, it has been shown that the repressive effect is much higher when the binding site for the miRNA is in the first 15 nt of the 3'UTR. This would match the hypothesis.... BLA BLA BLA

Targetscan Scores Jan ????

miBSdesigner

Very early we realized that having a binding site designer was crucial to complete the computational approach to our project: miBSdesigner is an easy-to-use application to create in silico binding sites for any given miRNA. By using our device, the user will be able to generate binding sites with several different properties.

Input

The user has to input a name for the miRNA to name the primers. The miRNA sequence must be 22 nucleotides long and has to be input in direction 5’ to 3’ (both DNA and RNA sequences are admitted and any extra characters will be removed from the sequence). The user can also enter a spacer inert sequence if he needs to place the binding site further along in the 3’UTR region (it is recommended that the binding site is at least 15 nucleotides away from the stop codon).Initially the user can choose between a perfect binding site (matching the 22 nucleotides), or an almost perfect binding site (matching all of the nucleotides, but leaving a 4-nucleotide bulge between 9 and 12. Apart from these two options, the user can personalize the binding site to meet their individual requirements.

Seed types

Figure 1: Interactions between two miRNAs and their binding sites. Examples to show different types of seeds.

In miBS designer, the user can choose between several types of seed for their binding site (ordered by increasing efficacy):

- 6mer (abundance 21.5%): only the nucleotides 2-7 of the miRNA match with the mRNA.

- 7merA1 (abundance 15.1%): the nucleotides 2-7 match with the mRNA, and there is an adenine in position 1.

- 7merm8 (abundance 25%): the nucleotides 2-8 match with the mRNA.

- 8mer (abundance 19.8%): the nucleotides 2-8 match with the mRNA and there is an adenine in position 1.

- Apart from any of these options, the user can decide to create a customized seed with a mismatch included.

The percentages of abundance are calculated among conserved mammalian sites for a highly conserved miRNA (Friedman et al. 2008)

Supplementary region

In miBS designer, the user can choose among several types of supplementary sequences, starting with 3 matching nucleotides (14-16), increasing sequentially until 8 (13-20), and then total matching (from 13-22, leaving a bulge). In case the user needs some other specific supplementary region, he can customize the sequence by inputting the desired matching nucleotides.

AU content

In order to allow the user to improve the efficacy of their binding sites, miBS designer offers options to increase the AU content by adding adenine or uracil to positions around the matches (specifically in -1, 0, 1, 8, 9 and 10). The function is designed so that it varies the AU content without introducing new pairings.

Sticky ends

In order to facilitate the task of introducing the binding site into a plasmid, the user can add sequences to both ends of the binding site. Initially, the user can choose among the RFC-12 standard for biobricks BB2, the XmaI/XhoI restriction enzymes used IN WHAT??, or some custom sequences input by the user. In the last case, the output sequences will not be directly ready for cloning: the user has to either digest the construction prior to ligation, or to process the primers before ordering them to remove the extra nucleotides.

Output

miBS designer generates the primer needed to integrate the binding site desired, into a plasmid, alongside with the primer for the complementary strand. It will also produce specific names for the two primers.

Neural Network Model

Neural Network theory

Artificial Neural Network usually called (NN), is a computational model that is inspired by the biological nervous system. The network is composed of simple elements called artificial neurons that are interconnected and operate in parallel. In most cases the NN is an adaptive system that can change its structure depending on the internal or(and?) external information that flows into the network during the learning process. The NN can be trained to perform a particular function by adjusting the values of the connection, called weights, between the artificial neurons. Neural Networks have been employed to perform complex functions in various fields, including pattern recognition, identification, classification, speech, vision, and control systems.

During the learning process, difference between the desired output (target) and the network output is minimised. This difference is usually called cost; the cost function is the measure of how far is the network output from the desired value. A common cost function is the mean-squared error and there are several algorithms that can be used to minimise this function. The following figure displays such a loop.

Figure 2: Training of a Neural Network.

Model description

Input/target pairs

The NN model has been created with the MATLAB NN-toolbox. The input/target pairs used to train the network comprise experimental and literature data (Bartel et al. 2007). The experimental data were obtained by measuring via luciferase assay the strength of knockdown due to the interaction between the shRNA and the binding site situated on the 3’UTR of luciferase gene. Nearly 30 different rational designed binding sites were tested and the respective knockdown strength calculated with the following formula->(formula anyone???).
Each input was represented by a four elements vector. Each element corresponded to a score value related to a specific feature of the binding site. The four features used to describe the binding site were: seed type, the 3’pairing contribution the AU-content and the number of binding site. The input/target pair represented the relationship between a particular binding site and the related percentage of knockdown. The NN was trained with a pool of 46 data. Afterwards it was used to predict percentages of knockdown given certain inputs. The predictions were then validated experimentally.

Characteristic of the Network

The neural network comprised two layers (multilayer feedforward Network). The first layer is connected with the input network and it comprised 15 artificial neurons. The second layer is connected to the first one and it produced the output. For the first and the second layer a sigmoid activation function and a linear activation function were used respectively. The algorithm used for minimizing the cost function (sum squared error) was Bayesian regularization. This Bayesian regularization takes place within the Levenberg-Marquardt algorithm. The algorithm updates the weight and bias values according to Levenberg-Marquardt optimization and overcomes the problem in interpolating noisy data, (MacKay 1992) by applying a Bayesian framework to the NN learning problem.

Figure 3: schematic illustration of the network components. Hidden represent the first layer and it comprised 15 artificial neurons, while output is the second and last layer producing the output. The symbol “w” was the representation of the weights and “b” of the biases.

Results

Training the Neural Network

The Network was trained with 46 samples. The regression line showing the correlation between the NN outputs and the targets was R=0.9864.



Figure 4: Regression line showing the correlation between the NN output and the respective target value.

Simulation and experimental verification

Fuzzy Inference Model

Why using a fuzzy inference system to model binding site efficiency?

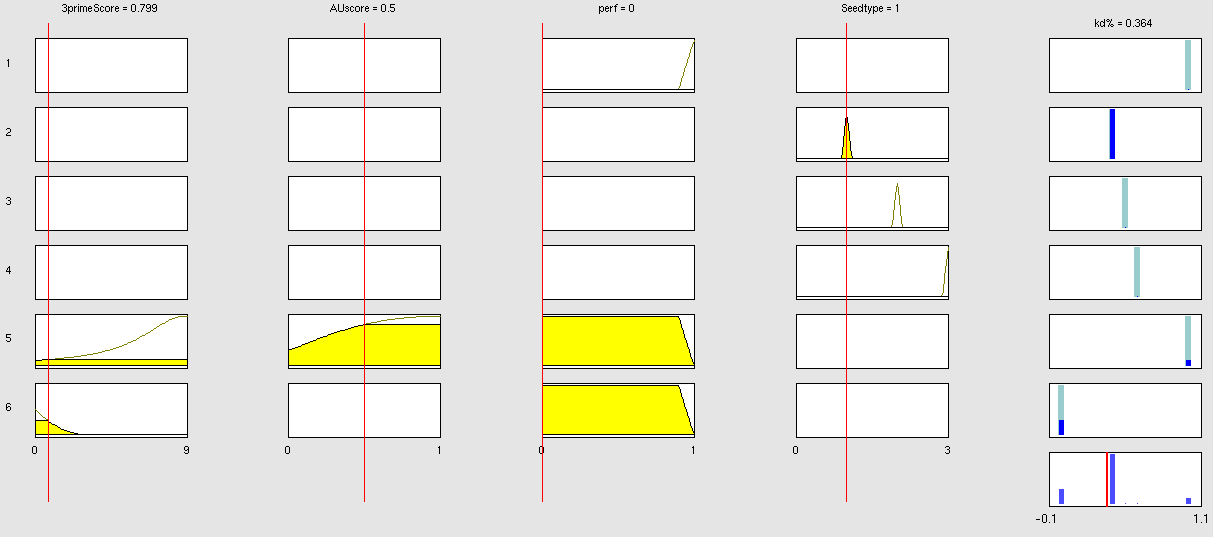
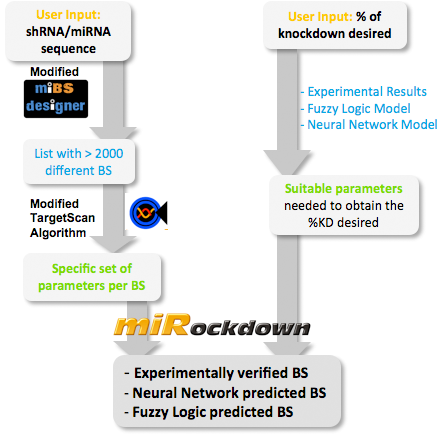
To be able to evaluate the complex features of an shRNA or miRNA binding site and predict a resulting knockdown percentage of the protein we developed a fuzzy inference system (fis). The parameterized properties of the binding sites serve as input and will be processed into the knockdown percentage as the single output. Thus our fuzzy inference system is characterized as a multiple input, single output fuzzy inference system (MISO). Fuzzy Logic is a rule-based approximate artificial reasoning method developed by Lotfi Zadeh in 1965. Its motivation is the observation that humans often think and communicate in a vague way, and yet can make precise decisions [Nelles O. Nonlinear System Identification Springer Verlag GmbH & Co., Berlin, 2000.]. It has been widely used in engineering and Artificial Intelligence approaches such as Fuzzy Controllers and Fuzzy Expert Systems. Fuzzy Logic has also been used for the modeling of biological pathways [Bosl W. J. Systems biology by the rules: hybrid intelligent systems for pathway modeling and discovery. BMC Systems Biology1:13 (2007).] and to analyze gene regulatory networks [Laschov D., Margaliot M. Mathematical modeling of the lambda switch:a fuzzy logic approach. J Theor Biol. 21:475-89 (2009)]. Key advantages of Fuzzy logic-based approaches are (i) the ability to construct models based on prior knowledge of the system and experimental data and (ii) encode intermediate states for inputs and outputs, thus improving other logic-approaches that can only deal with ON/OFF states such as Boolean models [Aldridge B. B., Saez-Rodriguez J., Muhlich J. L., Sorger P. K., Lauffenburger D. A. Fuzzy logic analysis of kinase pathway crosstalk in TNF/EGF/insulin-induced signaling PLoS Comput Biol.5:e1000340 (2009).] and (iii) simulations can be derived from both qualitative and quantitative data, both of which can be cast into the form of IF-THEN rules. Thus, FL constitutes a powerful approach for the understanding of heterogeneous datasets. 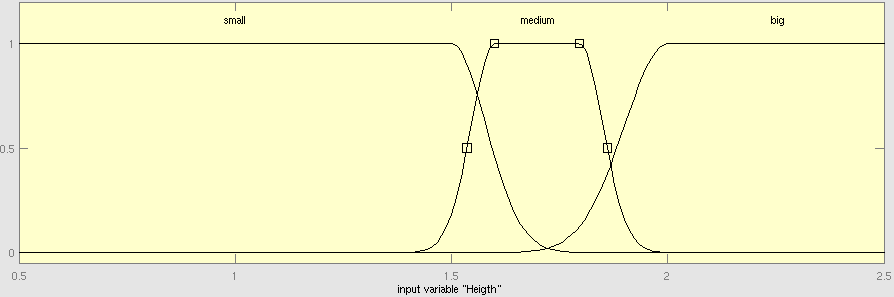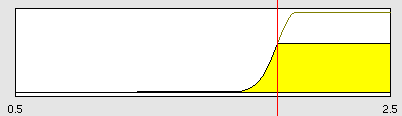Fuzzy inference systems are based on membership functions (MF). MF rate input parameters on a scale from 0 to 1, how much they satisfy a criterion. There can be one, or multiple criteria – called membership function - for one input parameter. The height of persons for example can be evaluated with one MF - how much the person satisfies being tall. On the other hand, there could be 3 MFs, one evaluating the membership to small people, the second to medium sized people and the third one to big people (Figure MembershipFunction1.png). In case of a persons height of 1.8 meter the MF “big” would be satisfied to about 0.6 (Figure MembershipFunctionBig.png). Like this, all input is converted to membership values from 0 to 1. Changing the shape of the MF gives the opportunity to have either functional dependencies, allowing intermediate states of the membership values, or simple ON/OFF states, where the membership value can be only 0 or 1 (Figure MembershipONOFF.png). Thus different kinds of input parameters can be evaluated with a fuzzy inference system. For the simple height example model the age of the person could be taken as second input and evaluated by a MF that is 0 until the age of 18 and 1 for older persons. Thus the model would differentiate between young and grown-up persons.

Simple if-then rules can then be used to combine the input MF to an output MF. The satisfaction of a rule by an object (set of input parameters) is defined by the degree of membership of the object to the different MF. The higher the satisfaction of the rule, the higher is the membership to the output MF. The output MF can be a function like the input MF. This is the case in Mamdani method fuzzy inference systems [Mamdani, E.H. and S. Assilian, "An experiment in linguistic synthesis with a fuzzy logic controller," International Journal of Man-Machine Studies, Vol. 7, No. 1, pp. 1-13, 1975.]. We are using a Sugeno method fuzzy inference system [Sugeno, M., Industrial applications of fuzzy control, Elsevier Science Pub. Co., 1985.], where the output MF is either a constant or a linear function depending on input parameters. The advantage of a Sugeno fuzzy inference system is, that it is computationally more efficient and easier to optimize or adapt due to the more simple output MF. Due to the non-intuitive combination of the 3'-pairing and AU-content score, our fuzzy inference system needs to be optimized computationally.

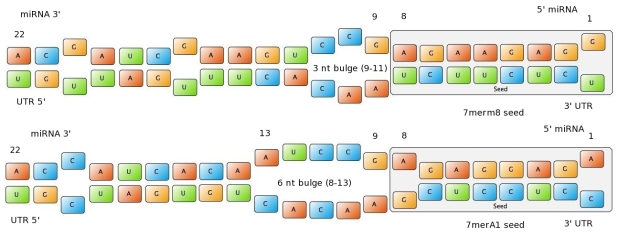
shRNA binding sites

3 MFs for height input
The height input is...

MF - "big"	MF for ON/OFF-system
bla	bla

Fuzzy Model Concepts

Bulged binding sites concept: This model concept evaluates bulged- or "near-perfect" binding sites separately from conventional seed + 3'-pairing binding sites. Rule number 2 considers the bulge-size of the bulged binding site.

Bulged binding sites (including AU-content-score) concept: This concept extends the bulged-BS concept with the addition of AU-content score evaluation. Therefore rule number 2 was modified accordingly.

Consider low 3' score concept: This model concept takes into consideration, that binding sites with a 3'-score under 3 did not show a significant change in knockdown efficiency compared to a control with only seed pairing [http://2010.igem.org/Team:Heidelberg/Modeling#References (Grimson et al., 2007)]. This is realized by rule number 6.

Strength: general prediction, no dependency on conditions. Assured by [normalization strategy]

We came up with different concepts of what kind of input parameters to integrate into the fuzzy inference model and how to evaluate them. Therefore we parameterized the properties of a large set of binding sites according to various different BS characteristics. The targetscan_50_context_scores – Algorithm [http://2010.igem.org/Team:Heidelberg/Modeling#References (Rodriguez et al., 2007)] which evaluates binding sites in respect to 3'-pairing and AU-content gives out a score that seems appropriate to distinguish especially between endogenous miRNA like binding sites. A more detailed description on the concept of binding site parameterization can be found under Model Training Set.

Fuzzy Model Optimization

[http://igem.bioquant.uni-heidelberg.de/igem_2010/FuzzyModelResults.html Click here, if you are interested in more recent model optimizations results!]

miRockdown on miBEAT

Right from the beginning of our modeling project, we knew we would have to integrate our trained models into an online GUI. We realized it in the most user friendly way we could think of: The user only needs to input the desired knockdown percentage (kd%) and choose an sh/miRNA sequence, to get a binding site that satisfies the users needs.

Overview of the miRockdown script flow. The knockdown percentage (kd%) input invokes the selection of the right experimental and model binding site or binding site parameters respectively. The binding site (BS) sequence input starts the generation of on the fly generated BS sequences, which are characterized by a modified targetscan_scores algorithm. The parameters of the selected model BS are correlated with the generated BS parameters and the most similar of the generated BS is the output.

The results of both of our models and the experimentally verified binding sites are integrated in [miRockdown] (see Figure: miRockdown) on the [miBEAT] GUI. For every binding site request of a user there are the results of the three different concepts displayed. Thus the users can always choose which of the three differently generated binding to use. The binding site with the most similar experimentally observed knockdown percentage is given out, together with its properties and oligos ready to clone into the miTuner-construct.
The binding sites generated from the model results come into play, when the user wants to use his or her own sh/miRNA, or when the experimentally verified binding sites have a knockdown, that is not sufficiently similar to the desired knockdown.
A script integrated into miRockdown will correlate the desired kd% with a database file for every model. The content of the database files consists of a set of binding site parameters objects spanning the complete range of the model input binding site parameters. Additionally the database files contain the models kd% result calculated for the whole set of objects.
With the user-chosen sh/miRNA sequence as input a binding site generator script is invoked, which varies the seed-type, 3'-pairing, AU-content and bulge-size of on the fly generated binding sites. The 3'-pairing and the AU-content score of the generated BS are characterized by a modified version of the targetscan_50_context_scores – Algorithm [http://2010.igem.org/Team:Heidelberg/Modeling#References (Rodriguez et al., 2007)]. The input and output functions were adapted to the mode of operation of miRockdown, thus no files have to be generated while running miRockdown.
Now, that the generated binding sites are completely characterized, they can be compared with the parameters of the suitable model BS. The generated BS that fits the parameters of the suitable model BS best is selected as the output BS of miRockdown.

Tissue specific miRNAs

Aastha

Integration into GUI

Aastha

References

[http://www.targetscan.org/cgi-bin/targetscan/data_download.cgi?db=vert_50 targetscan_50_context_scores.pl] Copyright(c) 2007,2008 Whitehead Institute for Biomedical Research. All Rights Reserved Joe Rodriguez, Robin Ge, Kim Walker, and George Bell