Team:Imperial College London/Modelling/Output/Detailed Description
From 2010.igem.org
(Many changes mainly in abandoned attempts) |
(ADDING DIFFERENTIAL EQNS.) |
||
| Line 184: | Line 184: | ||
<html><h2>2. Model preA: Simple production of dioxygenase</h2></html> | <html><h2>2. Model preA: Simple production of dioxygenase</h2></html> | ||
| + | |||
| + | This model was developed to illustrate 1-step amplification output. | ||
| + | |||
| + | <b>Elements of the system</b> | ||
| + | |||
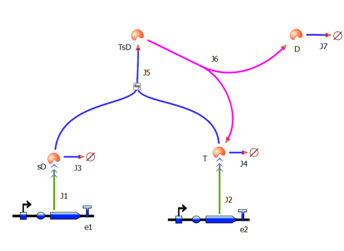
| + | #Dioxygenase (C230 chown <i>blue</i>) is the enzyme that starts getting produced upon activation signal (eg. detection of Schistosoma). | ||
| + | #Catechol (cat. shown <i>white with orange edge</i>) is artificially added chemical during the experiment. It is acted on by dioxygenase to produce yellow muconic acid. | ||
<div ALIGN=CENTER> | <div ALIGN=CENTER> | ||
{| style="background:#e1e1e1;text-align:center;font-family: helvetica, arial, sans-serif;color:#555555;margin- top:5px;padding: 2px;" cellspacing="5"; | {| style="background:#e1e1e1;text-align:center;font-family: helvetica, arial, sans-serif;color:#555555;margin- top:5px;padding: 2px;" cellspacing="5"; | ||
|- | |- | ||
| - | |[[Image: | + | |[[Image:1-step_amplification.png|700px]] |
|- | |- | ||
| - | |Transcription and translation | + | |Transcription and translation(simple production) of dioxygenase and its enzymatic activation of yellow colour. |
|} | |} | ||
</div> | </div> | ||
| + | <b>Interactions between elements</b> | ||
| + | |||
| + | The enzymatic interactions can be described in the following way: | ||
| + | |||
| + | <html> | ||
| + | <CENTER><img src="https://static.igem.org/mediawiki/2010/6/63/Catechol_Dioxygenase.png"alt="Catechol reacting with dioxygenase"/></CENTER> | ||
| + | </html> | ||
| + | Where: D is Dioxygenase, C is Catechol, C-D is catechol-dioxygenase transition complex, M<sub>a</sub> is Muconic acid - the yellow ouptput. | ||
| + | |||
| + | <b>Differential equations</b> | ||
| - | + | The above reaction can be written in terms of differential equations: | |
<html><h2>3. Model A: Activation of Dioxygenase by TEV enzyme</h2></html> | <html><h2>3. Model A: Activation of Dioxygenase by TEV enzyme</h2></html> | ||
Revision as of 15:56, 22 October 2010
| Temporary sub-menu: Objectives; Detailed Description; Parameters & Constants; Results & Conclusion;Download MatLab Files; |
| Output Amplification Model | ||||||||||||||||||||||||||||||
|
The following page presents the details of the models that have been developed. Firstly, assumptions that have been exploited are explained. Then every model is presented separately as each of them has slightly different elements of the system and the interactions between them. However, there are only 3 fundamental biochemical processes that will be analysed:
1. Law of Mass ActionDuring a meeting with our advisors, it was noted that our initial models (in which it was assumed that our system obeyed Michaelis-Menten kinetics) were wrong as the assumptions made by Michaelis-Menten approximation were not obeyed by the system. A few of Michaelis-Menten assumptions were not met by our system:
Since we are continuously producing enzyme, Vmax will change. Therefore the conservation E0 = E + ES does not hold for our system.
We are producing both substrate and enzyme, so we have approximately the same amount of substrate and enzyme.
Abandoned Initial Attempts
Elements of the system
Simple models
Implementation of Michaelis-Menten kinetics
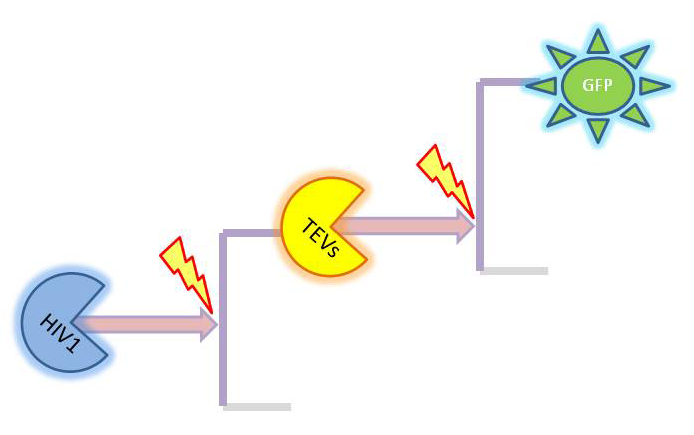
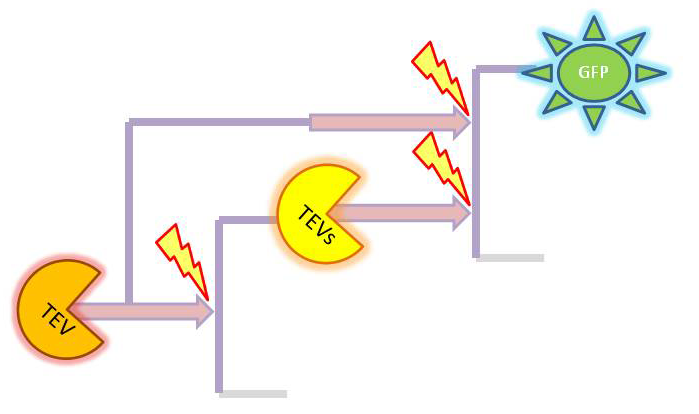
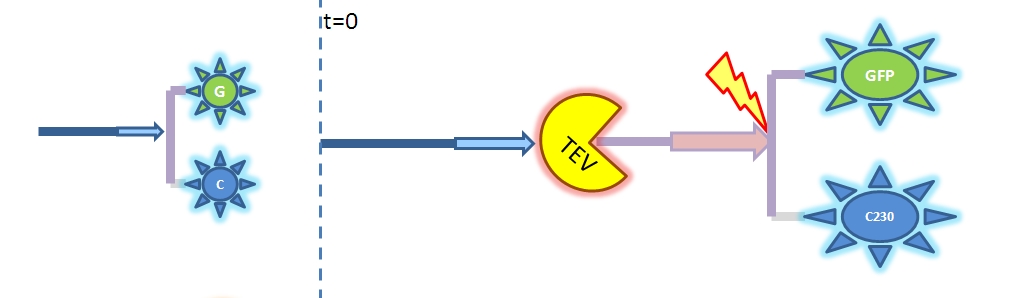
Conclusion We were not able to obtain all the necessary constants. Hence, we decided to make educated guesses about possible relative values between the constants as well as varying them and observing the change in output. As the result, we concluded that the amplification happens at each amplification level proposed. The magnitude of amplification varies depending on the constants. There is not much difference between using TEV or HIV1. Change of output During our literature research, we came across a better output, so we abandoned the idea of using GFP as an output. Instead, we are using catechol. An enzyme, dioxygenase, will be acting on the catechol, which will then result in a coloured output. Catechol will be added to the bacteria manually (i.e. the bacteria will not produce catechol). Hence, in our models dioxygenase will be treated as an output as this enzyme is the only activator of catechol in our system. This means that the change of catechol into its colourful form is dependent on the dioxygenase concentration. References
As we could not use the Michaelis-Menten simplification to model enzymatic reactions in our system, we will had to solve the problem from first principle. It meant referring to more general set of assumptions called Law of Mass Action. This allowed us to model our enzymatic reactions without making assumptions about amounts of particular species as long as the amounts are bigger than single molecule level. This resulted in bigger number of partial differential equations as there was one per each species instead of 1 per reaction. 2. Model preA: Simple production of dioxygenaseThis model was developed to illustrate 1-step amplification output. Elements of the system
Interactions between elements The enzymatic interactions can be described in the following way:
 Differential equations The above reaction can be written in terms of differential equations: 3. Model A: Activation of Dioxygenase by TEV enzyme
 This is a simple enzymatic reaction, where TEV is the enzyme, Dioxygenase the product and split Dioxygenase the substrate. Choosing k1, k2, k3 as reaction constants, the reaction can be rewritten in these four sub-equations:
 These four equations were implemented in Matlab, using a built-in function (ode45) which solves ordinary differential equations. Implementation in TinkerCell Another approach to model the amplification module would be to implement it in a program such as TinkerCell (or CellDesigner). This would be useful to check whether the Matlab model works. 4. Model B: Activation of Dioxygenase by TEV or activated split TEV enzymeThis version includes the following features:
5. Model C: Further improvementsThis model has not been implemented because of the conclusions that we reached from Models A and B. It would include the following features:
|
 "
"