Team:SDU-Denmark/project-m
From 2010.igem.org
(Difference between revisions)
m (→Physical Modelling) |
|||
| Line 7: | Line 7: | ||
=== 1. Motivation === | === 1. Motivation === | ||
| + | <p style="text-align: justify;"> | ||
One of the main ideas in the project is to control the flow induced by a bacterial carpet in a micro-tube. What we want to do in this part of the project is to study the mechanics of such a system, and how different parameters will affect it. One way to do this is to create a physical model, that describes the most essential features of the system. Our work connected to the development of such a model is presented in the following. The basis for any model is an understanding of the physical system in question, therefore we will start with a short review of the hydrodynamic properties of flagella and the bacterial pumping system constructed by [[https://2010.igem.org/Team:SDU-Denmark/project-m#Litterature 1]]. | One of the main ideas in the project is to control the flow induced by a bacterial carpet in a micro-tube. What we want to do in this part of the project is to study the mechanics of such a system, and how different parameters will affect it. One way to do this is to create a physical model, that describes the most essential features of the system. Our work connected to the development of such a model is presented in the following. The basis for any model is an understanding of the physical system in question, therefore we will start with a short review of the hydrodynamic properties of flagella and the bacterial pumping system constructed by [[https://2010.igem.org/Team:SDU-Denmark/project-m#Litterature 1]]. | ||
| - | + | </p> | |
=== 2. The real system === | === 2. The real system === | ||
| + | <p style="text-align: justify;"> | ||
So the "real" system that we want to model is a bacterial pump as described by [[https://2010.igem.org/Team:SDU-Denmark/project-m#Litterature 1]]. This is in principle just a small tube 15µm deep, 200µm wide and 15mm long, covered on the inside by a layer of flagellated bacteria. The bacterial layer described by [[https://2010.igem.org/Team:SDU-Denmark/project-m#Litterature 1]] is very dense and uniform, with a spacing between each bacterium of less that 1µm and 80% of the bacteria adhered to the surface as single bacteria. To get a better understanding of the origin of the created flow from this carpet, it is important to understand the structure of the bacterial flagellum. | So the "real" system that we want to model is a bacterial pump as described by [[https://2010.igem.org/Team:SDU-Denmark/project-m#Litterature 1]]. This is in principle just a small tube 15µm deep, 200µm wide and 15mm long, covered on the inside by a layer of flagellated bacteria. The bacterial layer described by [[https://2010.igem.org/Team:SDU-Denmark/project-m#Litterature 1]] is very dense and uniform, with a spacing between each bacterium of less that 1µm and 80% of the bacteria adhered to the surface as single bacteria. To get a better understanding of the origin of the created flow from this carpet, it is important to understand the structure of the bacterial flagellum. | ||
| Line 23: | Line 25: | ||
To summarize we have to model a very dense system of . This is indeed not a simple task, and quite a few simplification assumptions have to be made. These will be startingpoint of the next partXX | To summarize we have to model a very dense system of . This is indeed not a simple task, and quite a few simplification assumptions have to be made. These will be startingpoint of the next partXX | ||
| - | + | </p> | |
=== 3. Description of model === | === 3. Description of model === | ||
| - | + | <p style="text-align: justify;"> | |
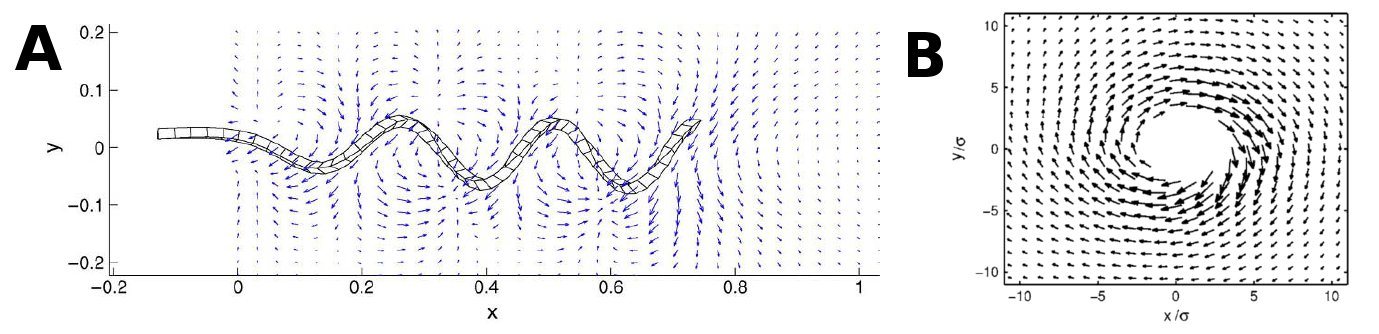
A flagellum creates propulsion by spinning around in a helical shape. Since the flagella/flagellabundles, take on a helical shape, the most accurate thing to do would be to model them as such, but doing this would become quite advanced for even one flagellum, not to mention an entire system. Since we are limited in both time and computerpower, we will have to clean it up a bit. | A flagellum creates propulsion by spinning around in a helical shape. Since the flagella/flagellabundles, take on a helical shape, the most accurate thing to do would be to model them as such, but doing this would become quite advanced for even one flagellum, not to mention an entire system. Since we are limited in both time and computerpower, we will have to clean it up a bit. | ||
| Line 65: | Line 67: | ||
As the above figures show, there is quite a difference depending on how many walls you take in to consideration. We decided to keep working with both the single-wall and the double-wall flowfields. | As the above figures show, there is quite a difference depending on how many walls you take in to consideration. We decided to keep working with both the single-wall and the double-wall flowfields. | ||
| - | + | </p> | |
=== 4. Flagella dynamics === | === 4. Flagella dynamics === | ||
| - | + | <p style="text-align: justify;"> | |
The next thing to be considered was how the flagella dependent on the fluid flow, ie. if we place a bacterium at an angle θ with the wall will it remain at that angle or will it get pulled around by the flow in the pipe, thus changing its position. The two extreme situations would be either that the flagella stick very hard to the surface and therefor is unaffected by the flow or that it is stick very gently to the surface and depent completely on the flow. In order to create an intermediate situation, we could constrain each flagellum with a harmonic potential, pulling it toward a favored angle(connected to the initial orientation of the fagella when stick to the surface). We believe the answer lies somewhere in between the two extremes, but that doesn't mean the extremes can't tell us anything. We therefore decided to create a model in which the flagella keep still, and one where they are affected by the flow and a potential. The size of the potential can always be set to zero if we want to study the flagella without it. | The next thing to be considered was how the flagella dependent on the fluid flow, ie. if we place a bacterium at an angle θ with the wall will it remain at that angle or will it get pulled around by the flow in the pipe, thus changing its position. The two extreme situations would be either that the flagella stick very hard to the surface and therefor is unaffected by the flow or that it is stick very gently to the surface and depent completely on the flow. In order to create an intermediate situation, we could constrain each flagellum with a harmonic potential, pulling it toward a favored angle(connected to the initial orientation of the fagella when stick to the surface). We believe the answer lies somewhere in between the two extremes, but that doesn't mean the extremes can't tell us anything. We therefore decided to create a model in which the flagella keep still, and one where they are affected by the flow and a potential. The size of the potential can always be set to zero if we want to study the flagella without it. | ||
| Line 95: | Line 97: | ||
In the end this model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after that the two velocity never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of computerpower we decided that instead of force calculations we would simpy find the flowvelocity at the tip of the flagellum and convert that directly to the angular velocity of the flagellum. | In the end this model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after that the two velocity never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of computerpower we decided that instead of force calculations we would simpy find the flowvelocity at the tip of the flagellum and convert that directly to the angular velocity of the flagellum. | ||
| - | + | </p> | |
=== 5. A 2-D model of the system === | === 5. A 2-D model of the system === | ||
| - | + | <p style="text-align: justify;"> | |
In this chapter we will present our model a bit more precisely and present some of the results it has given us. | In this chapter we will present our model a bit more precisely and present some of the results it has given us. | ||
| Line 122: | Line 124: | ||
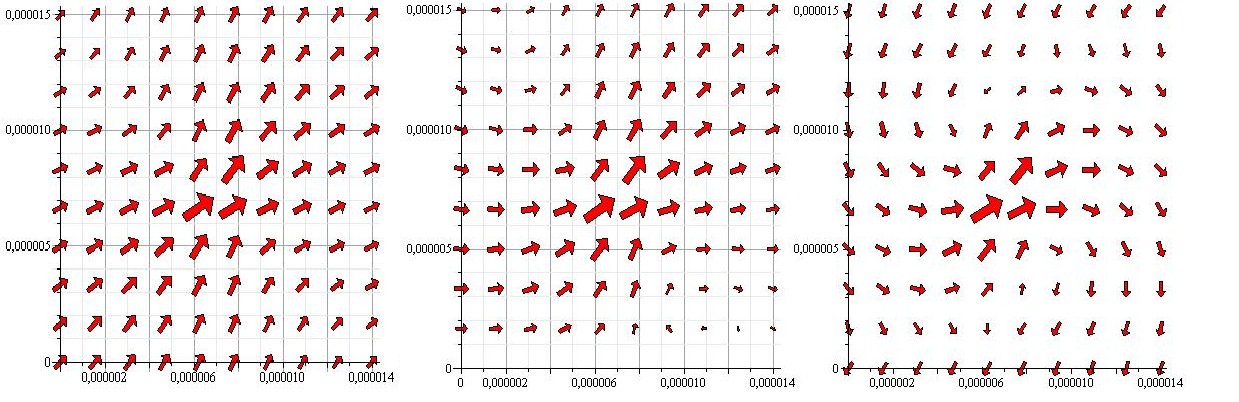
As the figure shows a very small deviation in the starting angle will cause a much bigger deviation in the end. The flagella in the systems used in this graph all lied down, but to which side the flagella went was highly dependent on the start konfiguration. When the mean angle was zero corresponding to a vertical flagellum it was pretty much 50-50, but when the start angles were pushed a bit to one side it had a tendency to shift the entire system in that direction. This tells us that if you can control the starting angle, it will go a long way towards creating a uniform flow. | As the figure shows a very small deviation in the starting angle will cause a much bigger deviation in the end. The flagella in the systems used in this graph all lied down, but to which side the flagella went was highly dependent on the start konfiguration. When the mean angle was zero corresponding to a vertical flagellum it was pretty much 50-50, but when the start angles were pushed a bit to one side it had a tendency to shift the entire system in that direction. This tells us that if you can control the starting angle, it will go a long way towards creating a uniform flow. | ||
| - | + | </p> | |
=== 6. A stationary 2-D model === | === 6. A stationary 2-D model === | ||
| - | + | <p style="text-align: justify;"> | |
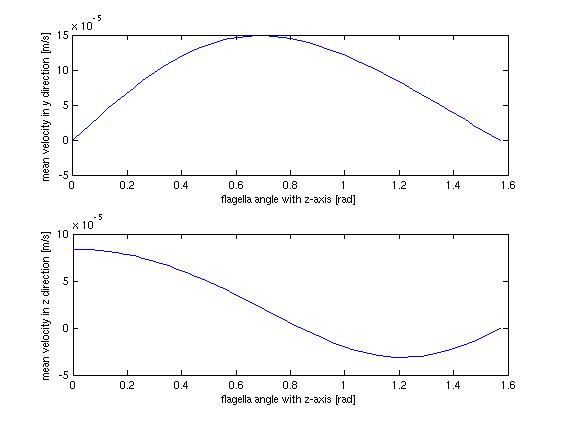
The stationary model, doesn't offer much when it comes to dynamics and interesting behavior, which shouldn't surprise anyone. It does however offer us the opportunity to investigate at which angle the flow in the direction of the tube is highest, which could be helpful when planning how to optimize the use of bacteria as a source of flow. | The stationary model, doesn't offer much when it comes to dynamics and interesting behavior, which shouldn't surprise anyone. It does however offer us the opportunity to investigate at which angle the flow in the direction of the tube is highest, which could be helpful when planning how to optimize the use of bacteria as a source of flow. | ||
| Line 130: | Line 132: | ||
The above figure shows the average flow velocity as a function of the angle of the flagella. In the abov case only one wall is taken in to account. The one of most importance is the top-one which shows the flow velocity parallel to the tube. According to these figures we get the best velocity at an angle of around 0.7 rad or approximately 40 degrees, where the angle is measured from the axis perpendicular to the wall. | The above figure shows the average flow velocity as a function of the angle of the flagella. In the abov case only one wall is taken in to account. The one of most importance is the top-one which shows the flow velocity parallel to the tube. According to these figures we get the best velocity at an angle of around 0.7 rad or approximately 40 degrees, where the angle is measured from the axis perpendicular to the wall. | ||
| - | + | </p> | |
=== 7. Model expansions === | === 7. Model expansions === | ||
=====3-D===== | =====3-D===== | ||
| + | <p style="text-align: justify;"> | ||
All programs we have written have been created for easy transfer from the 2-D model to a 3-D model. And we have made the adjustments needed in order for it to become 3-D, unfortunately we have not had time to check it for errors and to gain some results. | All programs we have written have been created for easy transfer from the 2-D model to a 3-D model. And we have made the adjustments needed in order for it to become 3-D, unfortunately we have not had time to check it for errors and to gain some results. | ||
| - | + | </p> | |
=====A flagella row on the other wall===== | =====A flagella row on the other wall===== | ||
| + | <p style="text-align: justify;"> | ||
In our model we settled for placing bacteria on one wall. During real-life application, flagella would most likely be placed on both walls. This is not something we have tried to implement in our model, though to do so should just be a matter of creating an extra grid an adapting the existing model a bit. If this was done it would go a long way towards improving the usability of the model | In our model we settled for placing bacteria on one wall. During real-life application, flagella would most likely be placed on both walls. This is not something we have tried to implement in our model, though to do so should just be a matter of creating an extra grid an adapting the existing model a bit. If this was done it would go a long way towards improving the usability of the model | ||
| - | + | </p> | |
===== A better double-wall approximation ===== | ===== A better double-wall approximation ===== | ||
| + | <p style="text-align: justify;"> | ||
The double-wall approximation we made is a very rough approximation based on what you do when you have a single wall. The model could be improved alot by making a better approximation, though aside from simply creating more mirror-pints, we have not investigated how this could be done, but it would most likely be quite difficult. | The double-wall approximation we made is a very rough approximation based on what you do when you have a single wall. The model could be improved alot by making a better approximation, though aside from simply creating more mirror-pints, we have not investigated how this could be done, but it would most likely be quite difficult. | ||
| - | + | </p> | |
=== Litterature === | === Litterature === | ||
| + | <p style="text-align: justify;"> | ||
1. M. J. Kim, K. S. Breuer, [http://microfluidics.engin.brown.edu/Breuer_Papers/Journals/Small2008_Bacterial_Pump.pdf Microfluidic pump powered by self-organizing bacteria], Small 4, 111-118. (2007) | 1. M. J. Kim, K. S. Breuer, [http://microfluidics.engin.brown.edu/Breuer_Papers/Journals/Small2008_Bacterial_Pump.pdf Microfluidic pump powered by self-organizing bacteria], Small 4, 111-118. (2007) | ||
| - | + | <br> | |
2. H.C. Berg, [http://www.annualreviews.org/eprint/cDJrS190m62mDRwHrlp9/full/10.1146/annurev.biochem.72.121801.161737 The rotary motor of bacterial flagella], Annu. Rev. Biochem. 72, 19-54. (2003) | 2. H.C. Berg, [http://www.annualreviews.org/eprint/cDJrS190m62mDRwHrlp9/full/10.1146/annurev.biochem.72.121801.161737 The rotary motor of bacterial flagella], Annu. Rev. Biochem. 72, 19-54. (2003) | ||
| - | + | <br> | |
3. H.C. Berg, E. coli in Motion, Springer, New York. (2004) | 3. H.C. Berg, E. coli in Motion, Springer, New York. (2004) | ||
| - | + | <br> | |
4. H. Floresa, E. Lobatonb, S. Méndez-Diezc, S. Tlupovad, R. Cortezd, A study of bacterial flagellar bundling, Bulletin of Mathematical Biology 67 137–168 begin_of_the_skype_highlighting 67 137–168 end_of_the_skype_highlighting. (2005) | 4. H. Floresa, E. Lobatonb, S. Méndez-Diezc, S. Tlupovad, R. Cortezd, A study of bacterial flagellar bundling, Bulletin of Mathematical Biology 67 137–168 begin_of_the_skype_highlighting 67 137–168 end_of_the_skype_highlighting. (2005) | ||
| - | + | <br> | |
5. M. Reicherta, H. Stark, Synchronization of rotating helices by hydrodynamic interactions, Eur. Phys. J. E 17, 493-500. (2005) | 5. M. Reicherta, H. Stark, Synchronization of rotating helices by hydrodynamic interactions, Eur. Phys. J. E 17, 493-500. (2005) | ||
| - | + | <br> | |
6. L. Turner, W. S. Ryu, H. C. Berg, Real-Time Imaging of Fluorescent Flagellar Filaments, JOURNAL OF BACTERIOLOGY, 2793–2801. (2000) | 6. L. Turner, W. S. Ryu, H. C. Berg, Real-Time Imaging of Fluorescent Flagellar Filaments, JOURNAL OF BACTERIOLOGY, 2793–2801. (2000) | ||
| - | + | <br> | |
7. http://commons.wikimedia.org/wiki/File:Flagellum_base_diagram.svg | 7. http://commons.wikimedia.org/wiki/File:Flagellum_base_diagram.svg | ||
| - | + | <br> | |
8. Nariya Uchida, Ramin Golestanian, Synchronization and Collective Dynamics in A Carpet of Microfluidic Rotors. (2009) | 8. Nariya Uchida, Ramin Golestanian, Synchronization and Collective Dynamics in A Carpet of Microfluidic Rotors. (2009) | ||
<br><br> | <br><br> | ||
| + | </p> | ||
<br> | <br> | ||
Revision as of 11:14, 21 October 2010
 "
"