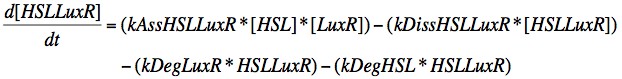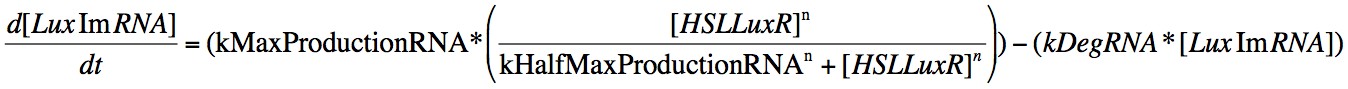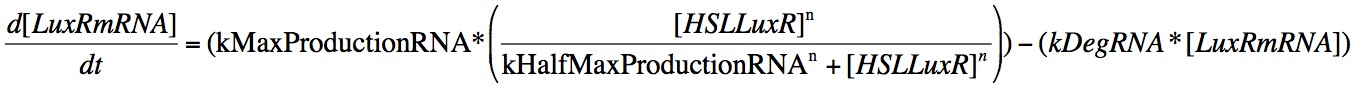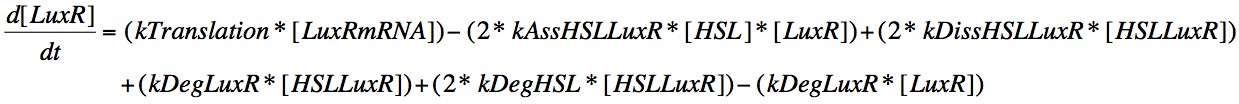Team:St Andrews/project/modelling/models/ODEs
From 2010.igem.org
(New page: {{:Team:St_Andrews/defaulttemplate}} <html> <h1> Ordinary Differential Equations (ODEs) </h1> </html> =The equations= n order to capture the behaviour behaviour mathematically, we devel...) |
|||
| Line 7: | Line 7: | ||
=The equations= | =The equations= | ||
| - | + | In order to capture the behaviour behaviour mathematically, we developed a system of 8 differential equations which together encapsulate the main behaviour of the LuxR circuit. Each equation represents the change in concentration of either a molecule or piece of mRNA with time, and all are first order. | |
'''1.''' [[Image:HSLLuxR2.jpg]] | '''1.''' [[Image:HSLLuxR2.jpg]] | ||
Revision as of 16:27, 13 September 2010


Ordinary Differential Equations (ODEs)
The equations
In order to capture the behaviour behaviour mathematically, we developed a system of 8 differential equations which together encapsulate the main behaviour of the LuxR circuit. Each equation represents the change in concentration of either a molecule or piece of mRNA with time, and all are first order.
Eqn. 1: The HSL-LuxR complex is broken apart when either HSL or LuxR degrades, or it may naturally dissociate at a rate kDissHSLLuxR. It is prodcued by the association of HSL and LuxR at a rate kAssHSLLuxR.
Eqn. 3: The production of LuxRmRNA is promoted by the HSL-LuxR complex. We model this behaviour using a Hill function controlled by the parameters kMaxProductionRNA and kHalfMaxProductionRNA.
Eqn. 5 : LuxI is translated from the mRNA at a reate kTranslation and degrades at a rate kDegRNA
Eqn. 6: LuxR is translated from its mRNA at a constant rate, kTranslation. It can also increase due to the dissociation of the HSL-LuxR complex or the degradation of the HSL or LuxR within the complex, which will result in those molecules which didn't degrade being included in the concentration present in the cell.
Eqn. 7: The GFP concentration is our primary indicator of activation of the quorum circuit. Similarly to LuxI it is produced from its respective mRNA at the rate kTranslation and degrades at a rate kDegGFP.
The above equations form the backbone of our model and are the framework on which all of our further work is based.
Our next issue was then to develop a method of simulating a change from low to high cell density in order to see if our model displayed the bistability that was theoreticaly predicted.
 "
"