Team:BCCS-Bristol/Modelling/BSIM/Geometric Modelling/Implementation
From 2010.igem.org
(→Computing Diffusion) |
|||
| Line 48: | Line 48: | ||
| - | The solution that we decided to use to implement the chemical field processing is an ‘octree’ [[Octrees]] | + | The solution that we decided to use to implement the chemical field processing is an ‘octree’ [[Team:BCCS-Bristol/Modelling/BSIM/Geometric_Modelling/Octrees]] |
structure. This is a hybrid between the two methods, though is more closely related to the finite | structure. This is a hybrid between the two methods, though is more closely related to the finite | ||
difference method. This uses a regular lattice of cubes, but changes the resolution of the lattice | difference method. This uses a regular lattice of cubes, but changes the resolution of the lattice | ||
Revision as of 13:32, 26 October 2010
iGEM 2010
Contents |
Implementation
Overview
There are two computational structures that need to take account of complex three dimensional structures if these features are to be implemented. One is the ability to represent a 3D shape inside the BSim environment, for example to provide a boundary, the other is the ability to represent a chemical field defined by such a 3D shape.
Representing 3D Shapes
In the early design phase of AgrEcoli, it quickly became evident that we would need to simulate some form of interaction between a bacterial population and its environment. Common analytical shapes (those that can be defined directly via a set of equations, for example a sphere) are somewhat limited when it comes to representing real-world objects. Fortunately there are a number of methods for specifying an arbitrary boundary in three dimensional space, such as through a set of parametric curves or via constructive solid geometry (often this involves combining a set of analytical shapes). However, the most common method throughout the field of computational geometry is to use a polyhedral mesh.
A polyhedral mesh can represent almost any three dimensional structure to an arbitrary degree of precision, so it was this type of 3D structure that we decided to use to represent boundaries. BSim currently supports arbitrary triangle-based meshes, which may contain both convex and concave regions as well as holes. Triangle meshes are the most common type of mesh output from computational geometry algorithms and from 3D modelling software, and are the simplest and most robust type of mesh one can use; almost any meshes of greater complexity can be simplified to a triangle mesh. BSim implements triangle meshes using a face-vertex representation internally. It currently supports direct import of .OBJ files, one of the most common file formats used for exchange of 3D mesh information, and standardised across the industry.
Collisions
As well as implementing meshes into BSim, we also added routines for computing collision events. This allows the user to detect when any object comes into contact with a mesh boundary and to respond as required. Although the default behaviour of BSim is to use the mesh as a boundary to restrict bacterial movement, it is trivial to add other responses. Possible complex responses include detecting the collision of chemicals, for example proteins, with a cell surface represented by a mesh boundary, or extending BSim to include biofilms.
Computing Diffusion
The diffusion of chemicals across the chemical field must be also computed. This involves solving a differential equation across an arbitrarily shaped 3D space. There are two broad classes of methods that are used to do this, finite element methods and finite difference methods.
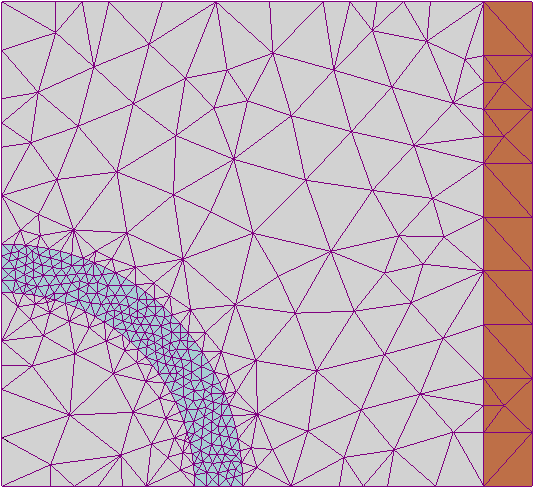
A finite element approach would use the mesh as a basis to generate a series of discrete units across which to calculate a discretized approximation system of ordinary differential equations. This is difficult to do reliably with arbitrary shapes. There exist several different algorithms that work well with different types of spaces (smooth, jagged, convex, concave) but it is difficult to implement a finite element method that works reliably in an arbitrary geometry without numerical instability. An example of a tessellation of triangles used to compute a finite element method approach can be seen in fig. 2(a). An accurate finite element model would converge to the analytical solution as the mesh became finer and finer, unfortunately this is difficult to do in generality, such a model which would be necessary for a robust addition to this modelling framework.
A finite difference method discretizes and computes a differential equation over a regular lattice, e.g. fig. 2(b) This means that it is much more numerically stable than the finite element method. The trade-off is that you have to partition the space along the lines of this regular grid. Which is not a very accurate representation of curves unless the resolution of the lattice is very high compared to the resolution of the curved object that you wanted to represent.
The solution that we decided to use to implement the chemical field processing is an ‘octree’ Team:BCCS-Bristol/Modelling/BSIM/Geometric_Modelling/Octrees
structure. This is a hybrid between the two methods, though is more closely related to the finite
difference method. This uses a regular lattice of cubes, but changes the resolution of the lattice
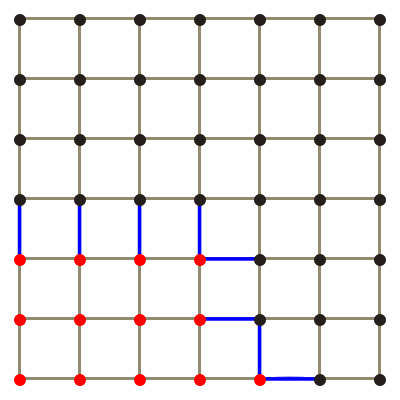
as it is partitioned by a mesh surface. This technique is visualized in fig. 10, note how the lattice
resolution increases around the sphere mesh, this allows for a more accurate division of the lattice
into a sphere shape. An octree structure will never be able to perfectly duplicate the shape of the
mesh that it is cast from, but the maximum resolution can be far higher than a regular lattice
with respect to its memory requirements because it only divides itself into a high resolution where
necessary.
 "
"