Team:Brown/Modeling/ODEs
From 2010.igem.org
(→ODE Modeling of the Quad-State circuit) |
(→ODE Modeling of the Quad-State circuit) |
||
| Line 21: | Line 21: | ||
=== Production of LovTAP === | === Production of LovTAP === | ||
| + | ==== Biological Process ==== | ||
| + | ==== Differential Equation ==== | ||
=== Production of LovTAP* === | === Production of LovTAP* === | ||
Revision as of 23:00, 24 October 2010
ODE Modeling of the Quad-State circuit
We formulated a system of differential equations which we used to model our system. As we have many players in our system and thus many equations, we chose to combine transcription and translation into single equations representing protein synthesis.
In all cases the equations represent the change in concentration in nanomoles/minute. Most equations make use of the Hill equation, which is used to model the cooperative binding of a ligand to a molecule. This is accomplished by describing the fraction of bound macromolecule as a function of ligand concentration.
We model induction by ligand X as: 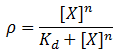
We model repression by ligand X as: 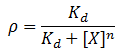
Where rho is the fraction of occupied ligand binding sites, [X] is the ligand concentration, n is the hill coefficient, and K_d is the equilibrium constant for dissociation.
We chose to simplify our model by expressing simultaneous repression/induction as the product of the corresponding hill equations. This is a simplification because it allows both the repressor and inducer to bind simultaneously, while in reality they are competing for available space.
 "
"