Team:BCCS-Bristol/Modelling/GRN/Results
From 2010.igem.org
m |
|||
| Line 7: | Line 7: | ||
==Phase Planes== | ==Phase Planes== | ||
| - | |||
| - | |||
[[Image:AgrEcoli_phase_plane.jpg|frameless|center|upright=4|Phase Plane of agrEcoli GRN with level curves]] | [[Image:AgrEcoli_phase_plane.jpg|frameless|center|upright=4|Phase Plane of agrEcoli GRN with level curves]] | ||
| Line 15: | Line 13: | ||
This diagram shows that a single stable solution exists, and that all trajectories converge to it eventually. This is unsurprising, as GFP, NsrR and mRNA all break down naturally. Therefore it makes sense that for any fixed production rate of any of these proteins, there will exist some point at which the rate of breakdown matches the rate of production, and the system reaches equilibrium. It is useful to confirm the existence of an equilibrium point mathematically, and locate it as a function of the constants in the equations. This allows predictions to be made about the behaviour of the system over time, avoiding the need for explicit experimental verification. | This diagram shows that a single stable solution exists, and that all trajectories converge to it eventually. This is unsurprising, as GFP, NsrR and mRNA all break down naturally. Therefore it makes sense that for any fixed production rate of any of these proteins, there will exist some point at which the rate of breakdown matches the rate of production, and the system reaches equilibrium. It is useful to confirm the existence of an equilibrium point mathematically, and locate it as a function of the constants in the equations. This allows predictions to be made about the behaviour of the system over time, avoiding the need for explicit experimental verification. | ||
| + | |||
| + | [[Image:AgrEcoli_nullclines.jpg|frameless|center|upright=4|Phase Plane of agrEcoli GRN with nullclines]] | ||
| + | |||
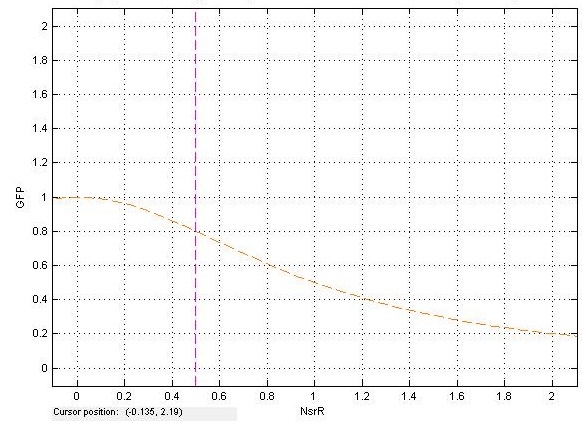
| + | The diagram above shows the nullclines of the NsrR/ GFP equations. These are lines in phase-space along which the rate of change of one of the variables is zero. The yellow line is for GFP, and the purple line is for NsrR. A point at which nullclines intersect is known as a ‘critical point’. Both lines are dashed, meaning that the trajectories are stable (i.e. all trajectories beginning on the nullcline travel towards our single critical point). Since all nullclines meeting at our only critical point are stable, we can classify the critical point itself as stable. Further, initial conditions starting exactly on the critical point will remain there for all time. | ||
Revision as of 17:39, 24 October 2010
iGEM 2010
Results
Phase Planes
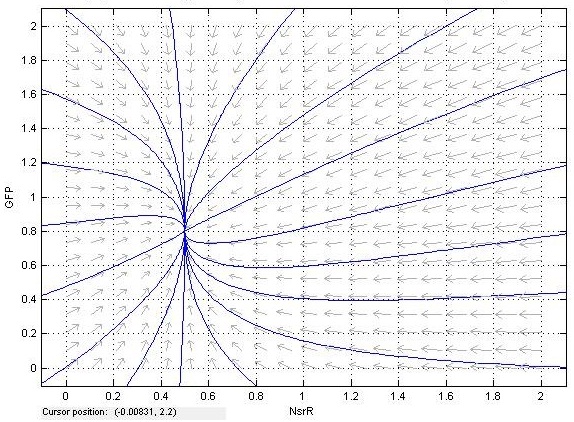
A two-dimensional phase plane diagram is a useful way of showing the dynamics of a system. The phase plane diagrams below show the rate of change of NsrR and GFP given the current quantity of each. This is shown as arrows on a plane, with the direction of the arrow signalling increase or decrease of a variable, and the size of the arrow describing the magnitude of the change. Also plotted on the diagram are level curves (blue). These represent the specific trajectory of some given initial conditions. Level curves are very useful to visualise a range of initial conditions.
This diagram shows that a single stable solution exists, and that all trajectories converge to it eventually. This is unsurprising, as GFP, NsrR and mRNA all break down naturally. Therefore it makes sense that for any fixed production rate of any of these proteins, there will exist some point at which the rate of breakdown matches the rate of production, and the system reaches equilibrium. It is useful to confirm the existence of an equilibrium point mathematically, and locate it as a function of the constants in the equations. This allows predictions to be made about the behaviour of the system over time, avoiding the need for explicit experimental verification.
The diagram above shows the nullclines of the NsrR/ GFP equations. These are lines in phase-space along which the rate of change of one of the variables is zero. The yellow line is for GFP, and the purple line is for NsrR. A point at which nullclines intersect is known as a ‘critical point’. Both lines are dashed, meaning that the trajectories are stable (i.e. all trajectories beginning on the nullcline travel towards our single critical point). Since all nullclines meeting at our only critical point are stable, we can classify the critical point itself as stable. Further, initial conditions starting exactly on the critical point will remain there for all time.
 "
"