Team:SDU-Denmark/project-m
From 2010.igem.org
(→3. Description of the model) |
(→4. Flagella dynamics) |
||
| Line 77: | Line 77: | ||
The basic idea now is that every flagella stuck to surface creates its own flowfield. To get the entire flowfield we add together all the flowfields created by the individual flagellum. In the case where the flagella are stationary that is basically it. For flagella that are able to move it's a bit more tricky. | The basic idea now is that every flagella stuck to surface creates its own flowfield. To get the entire flowfield we add together all the flowfields created by the individual flagellum. In the case where the flagella are stationary that is basically it. For flagella that are able to move it's a bit more tricky. | ||
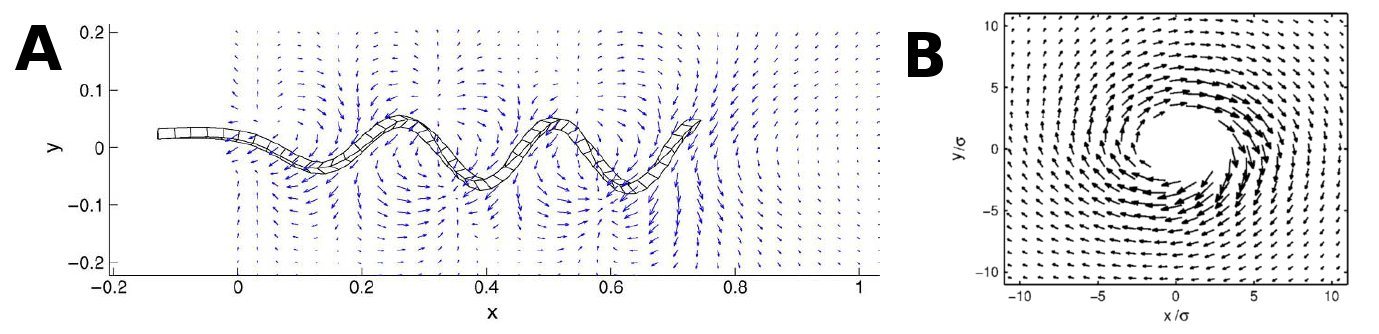
| - | The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the beads. | + | The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the beads. An image, showing some of the vectors involved and the procedure we used is shown below. |
| + | |||
| + | |||
| + | [[Image:Team-SDU-Denmark-flagel.jpg|center|700px]] | ||
| + | |||
First the fluid velocity at the given point is found. The method is the same whether there is 0, 1 or two walls, but the tensor used varies. | First the fluid velocity at the given point is found. The method is the same whether there is 0, 1 or two walls, but the tensor used varies. | ||
Revision as of 21:53, 23 October 2010
Physical Modelling
1. Motivation
One of the main ideas in the project is to control the flow induced by a bacterial carpet in a micro-tube. What we want to do in this part of the project is to study the mechanics of such a system, and how different parameters will affect it. One way to do this is to create a physical model, that describes the most essential features of the system. Our work connected to the development of such a model is presented in the following. The basis for any model is an understanding of the physical system in question, therefore we will start with a short review of the hydrodynamic properties of flagella and the bacterial pumping system constructed by [1].
2. The real system
So the "real" system that we want to model is a bacterial pump as described by [1]. This is in principle just a small tube 15µm deep, 200µm wide and 15mm long, covered on the inside by a layer of flagellated bacteria. The bacterial layer described by [1] is very dense and uniform, with a spacing between each bacterium of less that 1µm and 80% of the bacteria adhered to the surface as single bacteria. To get a better understanding of the origin of the created flow from this carpet, it is important to understand the structure of the bacterial flagellum.
The bacterial flagellum consists of 3 major parts, a rotary motor complex, a hook and a filament. The first part creates the rotary motion of the flagellum and the second part serves as a flexible coupling between the touque creating part and the filament. For our pourpose is the filament the most interesting part. This is responsible for the conversion of the rotary motion into a linear thust. The filament is a self-assembling polymeric structure composed of flagellin protein subunits. These are arranged in a circular way to create a hollow helical structure, with a typical width of 120-250Å and a length of 10-15µm.[2] A bacteria as E. coli typically has around 10 flagella.[3] These filaments are able to adopt a wide range of conformations under the induced torque. Numeric studies[4-5] and empiric results [6] suggest that the conformation is strongly dependent on the hydrodynamic environment that surrounds the flagellum and the direction of rotation. When several flagella rotates counterclockwise the flagella tends to bundle together in a single helix structure, due to the hydrodynamic interactions[4]. <<random biokemi!>> causes the flagella to turn clockwise instead at irregular intervals. This induces a sequence of deformations that changes flagella structure and unravels the bundle. This is known as tumble mode.
To be able to model the flow created by a bacterial carpet it is essential to know what kind of flowfield a single flagellum/bundle will create. This has primarily been investigated by numerical approach, where the flagella are modeled as semiflexible hookian systems. Several studies [4-5] suggests that the flow created from a single flagellum is highly non-uniform, but to some degree circular symmetric at the end of the flagellum (see figure XX and XX). When the flagella bundle together [4] suggests that this symmetry becomes less clear and flow becomes even more complicated.
All these results refers to flagella moving freely in aquas solution, the question now is wether the same is true for bacterial strick to the surface of a narrow tube? [6] suggests that bacteria compleatly fixed to a surface will deviate from the bundel behavior, but it is unclear what happens if the fixation is more partial or that the bacteria is sorrounded by a flow. To summarize we have to model a very dense system of . This is indeed not a simple task, and quite a few simplification assumptions have to be made. These will be startingpoint of the next partXX
3. Description of model
A flagellum creates propulsion by spinning around in a helical shape. Since the flagella/flagellabundles, take on a helical shape, the most accurate thing to do would be to model them as such, but doing this would become quite advanced for even one flagellum, not to mention an entire system. Since we are limited in both time and computerpower, we will have to clean it up a bit. One thing we can do is to consider all the flagella of a bacterium to form one bundle, even though doing so for a bacterium stuck to a wall is questionable. The overall result of this spinning bundle is that the bacterium moves in an almost straight line.This could be modelled as a pointforce on the tip of the flagellabundle pointing in the same direction as the bundle. The size of this force can be approximated by calculating the drag on a swimming bacterium. If the bacterium is considered almost spherical the drag force can be calculated by using the formula for stokes flow past a sphere:
where η(=8.94•10-4 Pa•s for water) is the viscosity of the fluid in which the bacterium is swimming, r(=0.4•10-6 m) is the radius of the bacterium and v(=50•10-6 m/s) is the velocity.
The dragforce and thereby the force created by the flagellabundle of one E. coli is
The system we are trying to model consists of a lot of bacteria stuck to a wall, but the part we are interested in is really the flagella and the forces they create. So we ignore the bodies of the bacteria, and instead consider the flagella as being stuck directly to the wall, with one end glued to the wall and the other pointing out into the fluid. Next step is to figure out what kind of flowfield, such a pointforce creates. The flowfield created by a pointforce in a fluid with no walls or other obstructions near it can be calculated using the corresponding Green's function known as the stokeslet.
where the three indices on G represent the number of walls and the matrix-coordinates. h is the distance between the pointforce and the wall and r is the vector from the pointforce to where the flow is to be calculated. If the pointforce is placed near a wall modifications must be made, since the flowvelocity has to go to zero at the boundary (known as the no-slip condition). This is done by using the Oseen-Blake tensor. Simply described what the Oseen-Blake tensor does, is to create a mirror image of our force on the other side of the wall, thus cancelling the flow near the wall. (This is not a completely accurate description, but rather an intuitive one.) In our case the flagella are stuck to a wall, so we'll be using the Oseen-Blake tensor.
Here R is the vector from the mirrorpoint of the force to the point where the flow is to be calculated. The two formulas above are based on [8] In our case the system we are trying to describe is a microtube. This means that the width of the tube is so small, that the forces created by the flagella are not only close to the wall to which the flagella are stuck, but also close to the opposite wall. This presents an interesting problem. Since the Oseen-Blake tensor works by creating a mirrorpoint of the real force on the opposite side of the wall, we will need a mirrorpoint behind the other wall if we are to uphold the no-slip condition. But the mirror forces also affect the flow near the other wall. In order to cancel this effect one could create another mirrorforce, corresponding to each of the mirror forces, but of course these would obstruct each other to, requirering yet more mirror forces. In the end we decided, to see how precise the system would be for one mirrorpoint behind each wall. This corresponds to taking the above equation and adding the three last terms once more, but with the mirrorvector corresponding to the other wall. The flowfield corresponding to this is shown below.
As the above figures show, there is quite a difference depending on how many walls you take in to consideration. We decided to keep working with both the single-wall and the double-wall flowfields.
4. Flagella dynamics
The next thing to be considered was how the flagella dependent on the fluid flow, ie. if we place a bacterium at an angle θ with the wall will it remain at that angle or will it get pulled around by the flow in the pipe, thus changing its position. The two extreme situations would be either that the flagella stick very hard to the surface and therefor is unaffected by the flow or that it is stick very gently to the surface and depent completely on the flow. In order to create an intermediate situation, we could constrain each flagellum with a harmonic potential, pulling it toward a favored angle(connected to the initial orientation of the fagella when stick to the surface). We believe the answer lies somewhere in between the two extremes, but that doesn't mean the extremes can't tell us anything. We therefore decided to create a model in which the flagella keep still, and one where they are affected by the flow and a potential. The size of the potential can always be set to zero if we want to study the flagella without it. The basic idea now is that every flagella stuck to surface creates its own flowfield. To get the entire flowfield we add together all the flowfields created by the individual flagellum. In the case where the flagella are stationary that is basically it. For flagella that are able to move it's a bit more tricky. The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the beads. An image, showing some of the vectors involved and the procedure we used is shown below.
First the fluid velocity at the given point is found. The method is the same whether there is 0, 1 or two walls, but the tensor used varies.
The dragforce created by the fluid on the bead is calculated using the same formula we used in chapter 3
Once we have the force we can use it to calculate the torque on the bead, we then summarize the torques of the individual beads to get the total torque
We then go to from the torque to the angular acceleration by dividing with the inertia. This is also where we introduce the potential, that we mentioned earlier
Now that we have the angular acceleration we can insert it into the equation of motion. This allows us to calculate the position of the flagella at the next timestep by using it's position at the current and at the previous timestep.
In the end this model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after that the two velocity never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of computerpower we decided that instead of force calculations we would simpy find the flowvelocity at the tip of the flagellum and convert that directly to the angular velocity of the flagellum.
5. A 2-D model of the system
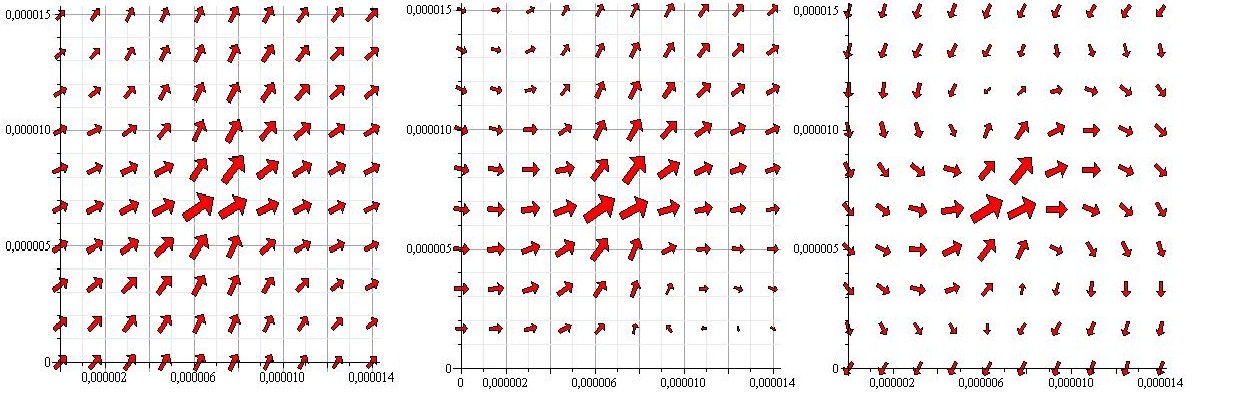
In this chapter we will present our model a bit more precisely and present some of the results it has given us. The 2-D model consists of a one dimensional grid, to which flagella are attached. Each flagellum produces a force which creates a flow which pushes every other flagellum, and thus a dynamic system is created. To calculate how big the flow will be at a given point, a vector from the tip of the force-producing flagellum to the point where you wish to know the flow must be created. To know how a flagellum is affected by the flow, the flow at the tip of the flagellum must be calculated. Once you have this vector and the vector corresponding to the force. The flow can be calculated using stokeslet or the Oseen-Blake tensor, depending on whether there is a wall nearby. In our system there is a wall so we will be using the Oseen-Blake tensor. This means that we are also required to find a vector from the mirrorpoint of the force, to the point at which we wish to know the flow. After this it is a matter of summarizing over all the flagella to find the total flowfield. The situation (disregarding the mirrorpoint) is sketched in figure XX. The completely velocity controlled equation of motion then becomes(using the notation in figure XX): The best way to illustrate the result from this model is to see it in action, so here follows the time series of a system af size 20 (only the 4 flagella in the middel of the system is shown), where the elastic constant is zero:
It is clear that the flagella tends to lie down and stabilize in an almost flat position in this case. In the following figure we have made a lot of these runs, but with varying average start-angle
As the figure shows a very small deviation in the starting angle will cause a much bigger deviation in the end. The flagella in the systems used in this graph all lied down, but to which side the flagella went was highly dependent on the start konfiguration. When the mean angle was zero corresponding to a vertical flagellum it was pretty much 50-50, but when the start angles were pushed a bit to one side it had a tendency to shift the entire system in that direction. This tells us that if you can control the starting angle, it will go a long way towards creating a uniform flow.
6. A stationary 2-D model
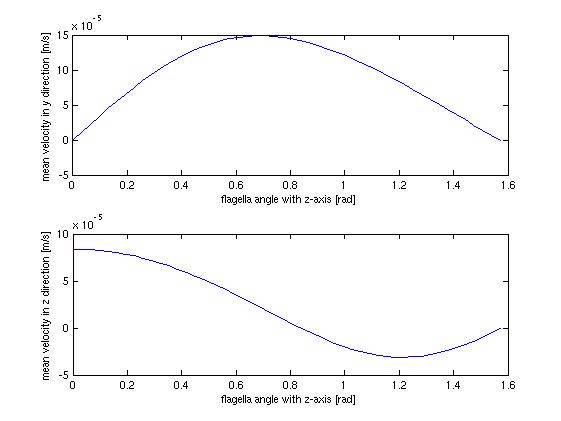
The stationary model, doesn't offer much when it comes to dynamics and interesting behavior, which shouldn't surprise anyone. It does however offer us the opportunity to investigate at which angle the flow in the direction of the tube is highest, which could be helpful when planning how to optimize the use of bacteria as a source of flow.
The above figure shows the average flow velocity as a function of the angle of the flagella. In the abov case only one wall is taken in to account. The one of most importance is the top-one which shows the flow velocity parallel to the tube. According to these figures we get the best velocity at an angle of around 0.7 rad or approximately 40 degrees, where the angle is measured from the axis perpendicular to the wall.
7. Model expansions
3-D
All programs we have written have been created for easy transfer from the 2-D model to a 3-D model. And we have made the adjustments needed in order for it to become 3-D, unfortunately we have not had time to check it for errors and to gain some results.
A flagella row on the other wall
In our model we settled for placing bacteria on one wall. During real-life application, flagella would most likely be placed on both walls. This is not something we have tried to implement in our model, though to do so should just be a matter of creating an extra grid an adapting the existing model a bit. If this was done it would go a long way towards improving the usability of the model
A better double-wall approximation
The double-wall approximation we made is a very rough approximation based on what you do when you have a single wall. The model could be improved alot by making a better approximation, though aside from simply creating more mirror-pints, we have not investigated how this could be done, but it would most likely be quite difficult.
Biochemical Modelling
1. Motivation
In order to create a flow with bacteria using their flagella movement as the motor it is important to understand bacterial motility and the effects our gen blande noget have on it.
Bacterial motion resembles a random walk, with periods of smooth swimming interrupted by brief tumbles that change the swimming direction. Chemotaxis is achieved by modulation of the tumbling frequency.
In our case we have added phototaxis to E. coli cells making them react to light as well as chemical gradients.
By creating a model describing the key features of the system it will be possible to study the Biochemical behaviour of such a system, and how different parameters will affect it. Before it is implemented in a bacterial strain.
2. The real system
Several chemosensory systems exists in bacteria, the one most studied is the chemotaxis of E. coli. Polar clusters of membrane-spanning methyl accepting chemotaxis proteins (MCPs) are positioned in the ends of the rod shaped E. coli.
Tar (responding to aspartate), Tsr (responding to serine), Tap (responding todipetides), Trg (responding to galactose) ang Aer (responding to oxygen) are the most common receptors seen in E. coli strains.
Transduction of the signal between the MCPs and the flagella motor are managed by a particular fined tuned signalling cascade, which is governed by several intracellular proteins.
Chemotaxis consists of three important phases reaction, adaptation and relaxation. In the reaction phase one of the MCPs sence the specific chemical gradient it responds to, the membrane protein activates the CheW enzym.
The active CheW enzyme suppresses the auto-phophorylation of the CheA enzyme, when no or only a small amount of CheA enzymes are phosphorylated, no phophorylation of the CheY and CheB enzyme accurse, which in the end increases run, because its phosphorylated CheY that binds to the flagella motors and induce tumbling.
When the bacteria have reached the area with a higher concentration of the chemical creating the gradient adaptation sets in.
Because no CheB have been phosphorylated during the reaction period CheR is “allowed” to methylate the MCPs, which increases the auto-phophorylation of the CheA enzyme. The indcreas in auto-phophorylation of CheA results in phophorylation of CheY that leads to tumbling of the bacteria. In the last phase relaxation the CheB have again been phosphorylated by CheA and are now able to demethylate the MCPs, returning the bacteria to its normal run/tumble frequency with a 0,1 second long tumbling period every 1 second.
One other thing to consider in the model is the distance from the to the flagella motors that are randomly located on the entire cell body.
Several modelling methods have been proposed to nearly all of the models include these four items:
“Attractant is assumed to be in axcess and binding is assumed to be rapid. One of the most common receptor types to be modelled is the Tar receptor.
This is not unexpected given that a large degree of the experimental literature has focused on the response of E. coli to aspirate which is detected by this receptor. Tar is also one of the most abundant receptors within the cytoplasmic membrane.
In models which have focused on the adaptation and/or the phosphorylation cascade, receptors are commonly modeled as complexes consisting of MCP, CheW and CheA. This is justified by the tight association of CheW and CheA to the MCP recptors.
3. Description of the model
The model of the system we will be using to predict biochemical behaviour of the system is a simplification of the real system.
The simplified model doesn’t consider the normal metabolism in the cell it only includes the most important enzymes in the normal E. coli chemotaxis pathway and the proteins responsible for coupling the phototaxis to the chemotaxis.
Beneath you will se a schematics over the system modelling was performed on, the enzymes and proteins with a red cross over them have not been modelled as a differential equation but considered as an constant in the system.
The important enzymes in the system is mathematically represented by a differential equation under the assumption of steady state in the system and modelled in a demo version of the program [http://www.berkeleymadonna.com/ Berkeley Madonna].
When light hits the receptor SRII the signal is transduced thuogth the HTRII and TSR on to the enzyme CheW and activates it, because it’s a straight forward signal transduction the proteins SRII and HTRII is not considered in the model and the equation for the activation of CheW is:
When the CheW enzyme is activated it induces auto-phophorylation of CheA, the phosphorylated CheA can phosphorylate the enzymes CheY and CheB, the equation for CheAp concentration is given by:
Phosphorylated CheY is produced by phophorylation of CheA and removed by CheZ which in this model is defined by a constant, this can be described mathematically by this equation:
Phosphorylated CheB is produced by phophorylation of CheA removed when TSRm is demethylated, this can be described mathematically by this equation:
Methylated TSR is constantly produced by the CheR enzyme which in this model is a constant, the demethylation is preformed by CheBp, the TSRm concentration can bescribed by this equation:
4. Model results
Litterature
1. M. J. Kim, K. S. Breuer, [http://microfluidics.engin.brown.edu/Breuer_Papers/Journals/Small2008_Bacterial_Pump.pdf Microfluidic pump powered by self-organizing bacteria], Small 4, 111-118. (2007)
2. H.C. Berg, [http://www.annualreviews.org/eprint/cDJrS190m62mDRwHrlp9/full/10.1146/annurev.biochem.72.121801.161737 The rotary motor of bacterial flagella], Annu. Rev. Biochem. 72, 19-54. (2003)
3. H.C. Berg, E. coli in Motion, Springer, New York. (2004)
4. H. Floresa, E. Lobatonb, S. Méndez-Diezc, S. Tlupovad, R. Cortezd, A study of bacterial flagellar bundling, Bulletin of Mathematical Biology 67 137–168. (2005)
5. M. Reicherta, H. Stark, Synchronization of rotating helices by hydrodynamic interactions, Eur. Phys. J. E 17, 493-500. (2005)
6. L. Turner, W. S. Ryu, H. C. Berg, Real-Time Imaging of Fluorescent Flagellar Filaments, JOURNAL OF BACTERIOLOGY, 2793–2801. (2000)
7. http://commons.wikimedia.org/wiki/File:Flagellum_base_diagram.svg
8. Nariya Uchida, Ramin Golestanian, Synchronization and Collective Dynamics in A Carpet of Microfluidic Rotors. (2009)
We know what we expect from our system, but does the math agree?
Contents |
 "
"