Team:SDU-Denmark/project-m

Physical Modeling

1. Motivation

One of the main ideas in the project is to control the flow induced by a bacterial carpet in a micro-tube. This is done by changing the tumble frequency of the bacteria when they are exposed to light. It is however not clear what the exact connection between the tumble frequency and the overall liquid flow is. This matter is complicated by the fact that the bacterial pump itself is a selforganizing system and changing the tumbling of the bacterial could therefore change the structure of the overall system completely. One way to assess this connection between tumble frequency and the flow is to create a physical model, that describes the most essential features of the system. Our work connected to the development of such a model is presented in the following. The basis for any model is an understanding of the physical system in question, therefore we will start with a short review of the hydrodynamic properties of flagella and the bacterial pumping system constructed by [1].

2. The real system

So the "real" system that we want to model is a bacterial pump as described by [1]. This is in principle just a small tube 15µm deep, 200µm wide and 15mm long, covered on the inside by a layer of flagellated bacteria. The bacterial layer described by [1] is very dense and uniform, with a spacing between each bacterium of less that 1µm and 80% of the bacteria adhered to the surface as single bacteria. To get a better understanding of the origin of the created flow from this carpet, it is important to understand the structure of the bacterial flagellum.

The bacterial flagellum consists of 3 major parts, a rotary motor complex, a hook and a filament. The first part creates the rotary motion of the flagellum and the second part serves as a flexible coupling between the touque creating part and the filament. For our pourpose is the filament the most interesting part. This is responsible for the conversion of the rotary motion into a linear thust. The filament is a self-assembling polymeric structure composed of flagellin protein subunits. These are arranged in a circular way to create a hollow helical structure, with a typical width of 120-250Å and a length of 10-15µm.[2] A bacteria as E. coli typically has around 10 flagella.[3] These filaments are able to adopt a wide range of conformations under the induced torque. Numeric studies[4-5] and empiric results [6] suggest that the conformation is strongly dependent on the hydrodynamic environment that surrounds the flagellum and the direction of rotation. When several flagella rotates counterclockwise the flagella tends to bundle together in a single helix structure, due to the hydrodynamic interactions[4]. <<random biokemi!>> causes the flagella to turn clockwise instead at irregular intervals. This induces a sequence of deformations that changes flagella structure and unravels the bundle. This is known as tumble mode.

A, shows a shematic picture of [7]. B and C shows respectively the flagella of a bacteria stuck to a surface and flagella bundels of a moving bacteria[6].

To be able to model the flow created by a bacterial carpet it is essential to know what kind of flowfield a single flagellum/bundle will create. This has primarily been investigated by numerical approach, where the flagella are modeled as semiflexible hookian systems. Several studies [4-5] suggests that the flow created from a single flagellum is highly non-uniform, but to some degree circular symmetric at the end of the flagellum (see figure XX and XX). When the flagella bundle together [4] suggests that this symmetry becomes less clear and flow becomes even more complicated.

All these results refers to flagella moving freely in aquas solution, the question now is wether the same is true for bacterial strick to the surface of a narrow tube? [6] suggests that bacteria compleatly fixed to a surface will deviate from the bundel behavior, but it is unclear what happens if the fixation is more partial or that the bacteria is sorrounded by a flow.

To summarize we have to model a very dense system of . This is indeed not a simple task, and quite a few simplification assumptions have to be made. These will be startingpoint of the next partXX

3. Description of model

A flagellum creates propulsion by spinning around in a helical shape. Since the flagella/flagellabundles, take on a helical shape, the most accurate thing to do would be to model them as such, but doing this would become quite advanced for even one flagellum, not to mention an entire system. Since we are limited in both time and computerpower, we will have to clean it up a bit.

One thing we can do is to consider all the flagella of a bacterium to form one bundle, even though doing so for a bacterium stuck to a wall is questionable. The overall result of this spinning bundle is that the bacterium moves in an almost straight line.This could be modelled as a pointforce on the tip of the flagellabundle pointing in the same direction as the bundle. The size of this force can be approximated by calculating the drag on a swimming bacterium. If the bacterium is considered almost spherical the drag force can be calculated by using the formula for stokes flow past a sphere:

F_d = -6πηrv

where η(=8.94•10^-4 Pa•s for water) is the viscosity of the fluid in which the bacterium is swimming, r(=0.4•10^-6 m) is the radius of the bacterium and v(=50•10^-6 m/s) is the velocity.

The dragforce and thereby the force created by the flagellabundle of one e. coli is

|F_d| = 3.37•10^-13 N.

The system we are trying to model consists of a lot of bacteria stuck to a wall, but the part we are interested in is really the flagella and the forces they create. So we ignore the bodies of the bacteria, and instead consider the flagella as being stuck directly to the wall, with one end glued to the wall and the other pointing out into the fluid.

Next step is to figure out what kind of flowfield, such a pointforce creates. The flowfield created by a pointforce in a fluid with no walls or other obstructions near it can be calculated using the corresponding Green's function known as the stokeslet.

If the pointforce is placed near a wall modifications must be made, since the flowvelocity has to go to zero at the boundary (known as the no-slip condition). This is done by using the Oseen-Blake tensor. Simply described what the Oseen-Blake tensor does, is to create a mirror image of our force on the other side of the wall, thus cancelling the flow near the wall. 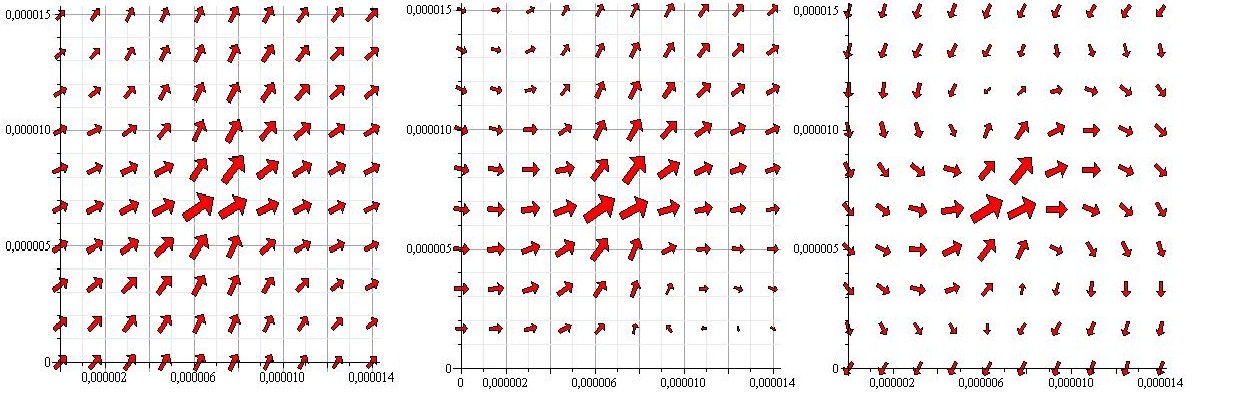(This is not a completely accurate description, but rather an intuitive one.) In our case the flagella are stuck to a wall, so we'll be using the Oseen-Blake tensor. A flowfield corresponding to this is shown below.

In our case the system we are trying to describe is a microtube. This means that the width of the tube is so small, that the forces created by the flagella are not only close to the wall to which the flagella are stuck, but also close to the opposite wall. This presents an interesting problem. Since the Oseen-Blake tensor works by creating a mirrorpoint of the real force on the opposite side of the wall, we will need a mirrorpoint behind the other wall if we are to uphold the no-slip condition. But the mirror forces also affect the flow near the other wall. In order to cancel this effect one could create another mirrorforce, corresponding to each of the mirror forces, but of course these would obstruct each other to, requirering yet more mirror forces. In the end we decided, to see how precise the system would be for one mirrorpoint behind each wall. The flowfield corresponding to this is shown below.

All 3 images show the flowfield created by a pointforce at (0.000007,0.000007) with an angle of 45 degrees with the x-axis. In the first image there are no walls. In the 2nd a wall is placed at y=0. In the 3rd one wall is placed at y=0 and one at y=0.000015

As the above figures show, there is quite a difference depending on how many walls you take in to consideration. We decided to keep working with both the single-wall and the double-wall flowfields.

4. Flagella dynamics

The next thing to be considered was how the flagella dependent on the fluid flow, ie. if we place a bacterium at an angle θ with the wall will it remain at that angle or will it get pulled around by the flow in the pipe, thus changing its position. The two extreme situations would be either that the flagella stick very hard to the surface and therefor is unaffected by the flow or that it is stick very gently to the surface and depent completely on the flow. In order to create an intermediate situation, we could constrain each flagellum with a harmonic potential, pulling it toward a favored angle(connected to the initial orientation of the fagella when stick to the surface). We believe the answer lies somewhere in between the two extremes, but that doesn't mean the extremes can't tell us anything. We therefore decided to create a model in which the flagella keep still, and one where they are affected by the flow and a potential. The size of the potential can always be set to zero if we want to study the flagella without it.

The basic idea now is that every flagella stuck to surface creates its own flowfield. To get the entire flowfield we add together all the flowfields created by the individual flagellum. In the case where the flagella are stationary that is basically it. For flagella that are able to move it's a bit more tricky.

The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the beads.

<equation of motion>

This model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after that the two velocity never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of computerpower we decided that instead of force calculations we would simpy find the flowvelocity at the tip of the flagellum and convert that directly to the angular velocity of the flagellum.

5. A 2-D model of the system

First, we will make a model consisting of a 1D-grid, afterwards we will expand it to 2D.

1D-model indsæt billede her

What we do from here is that we neglect the body of the bacteria. Instead we imagine that the flagella are glued to the surface off the pipe in such a way that they

<math>\coprod_{i=1}^N x_i</math>

Litterature

1. M. J. Kim, K. S. Breuer, [http://microfluidics.engin.brown.edu/Breuer_Papers/Journals/Small2008_Bacterial_Pump.pdf Microfluidic pump powered by self-organizing bacteria], Small 4, 111-118. (2007)

2. H.C. Berg, [http://www.annualreviews.org/eprint/cDJrS190m62mDRwHrlp9/full/10.1146/annurev.biochem.72.121801.161737 The rotary motor of bacterial flagella], Annu. Rev. Biochem. 72, 19-54. (2003)

3. H.C. Berg, E. coli in Motion, Springer, New York. (2004)

4. H. Floresa, E. Lobatonb, S. Méndez-Diezc, S. Tlupovad, R. Cortezd, A study of bacterial flagellar bundling, Bulletin of Mathematical Biology 67 137–168. (2005)

5. M. Reicherta, H. Stark, Synchronization of rotating helices by hydrodynamic interactions, Eur. Phys. J. E 17, 493-500. (2005)