Team:SDU-Denmark/project-m
From 2010.igem.org
(Difference between revisions)
(→A 2-D model of the system) |
m (→Description of model) |
||
| (12 intermediate revisions not shown) | |||
| Line 66: | Line 66: | ||
</p> | </p> | ||
<br> | <br> | ||
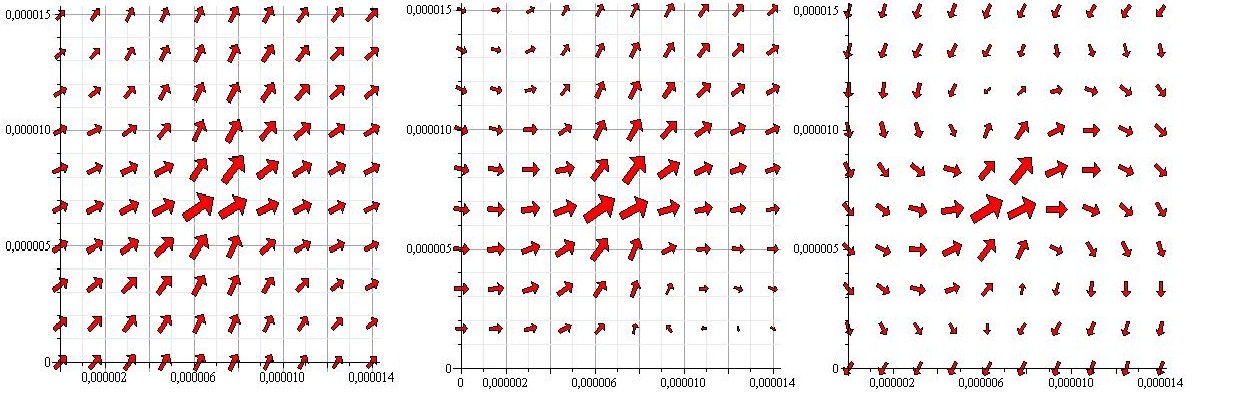
| - | [[Image:Team-SDU-Denamrk-Pointforces_notxt.jpg|thumb|center|580px|'''Figure 3''' All 3 images show the flowfield created by a pointforce at (0.000007,0.000007) with an angle of 45 degrees with the x-axis. In the first image there are no walls. In the 2nd a wall is placed at y=0. In the 3rd one wall is placed at y=0 and one at y=0.000015]] | + | [[Image:Team-SDU-Denamrk-Pointforces_notxt.jpg|thumb|center|580px|'''Figure 3''': All 3 images show the flowfield created by a pointforce at (0.000007,0.000007) with an angle of 45 degrees with the x-axis. In the first image there are no walls. In the 2nd a wall is placed at y=0. In the 3rd one wall is placed at y=0 and one at y=0.000015]] |
<p style="text-align: justify;"><br> | <p style="text-align: justify;"><br> | ||
As the above figures show, there is quite a difference depending on how many walls you take into consideration. We decided to keep working with both the single-wall and the double-wall flowfields. | As the above figures show, there is quite a difference depending on how many walls you take into consideration. We decided to keep working with both the single-wall and the double-wall flowfields. | ||
| Line 73: | Line 73: | ||
=== Flagella dynamics === | === Flagella dynamics === | ||
<p style="text-align: justify;"> | <p style="text-align: justify;"> | ||
| - | The next thing to be considered was how the flagella | + | The next thing to be considered was how the flagella depend on the fluid flow, i.e. if we place a bacterium at an angle θ with the wall, will it remain at that angle or will it get pulled around by the flow in the tube, thus changing its position? The two extreme situations would be either that the flagella stick very hard to the surface and are therefore unaffected by the flow or that they stick very gently to the surface and that their angle depends completely on the flow. In order to create an intermediate situation, we could constrain each flagellum with a harmonic potential, pulling it toward a favored angle (connected to the initial orientation of the fagella when it stick to the surface). We believe the answer lies somewhere in between the two extremes, but that does not mean the extremes can't tell us anything. We therefore decided to create a model in which the flagella keep still, and one where they are affected by the flow and a potential. The size of the potential can always be set to zero if we want to study the flagella without an affecting potential. |
<br><br> | <br><br> | ||
The basic idea then is that every flagella stuck to the surface creates their own flowfields. To get the entire flowfield we add together all the flowfields created by the individual flagella. In the case where the flagella are stationary the assumptions made so far actually shows the system. For flagella that are able to move it's a bit more tricky.<br> | The basic idea then is that every flagella stuck to the surface creates their own flowfields. To get the entire flowfield we add together all the flowfields created by the individual flagella. In the case where the flagella are stationary the assumptions made so far actually shows the system. For flagella that are able to move it's a bit more tricky.<br> | ||
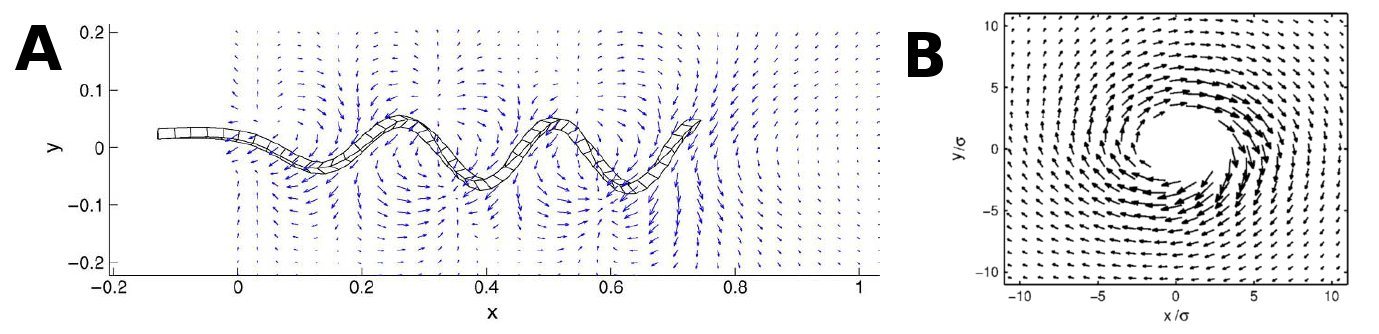
| - | The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the spheres. An image, showing some of the vectors involved and the procedure we used is shown below. | + | The first thing we had to figure out was how the flow created by all of the other flagella would affect one single flagellum. To do this we decided to approximate a flagellum as a string of spheres and use dragforce calculations to figure out the force with which the flowfields of the other flagella would affect the spheres. An image, showing some of the vectors involved and the procedure we used is shown below. <br> |
[[Image:Team-SDU-Denmark-flagel.jpg|thumb|center|580px|'''Figure 4''': Sketch of the principial structure of the model.]] | [[Image:Team-SDU-Denmark-flagel.jpg|thumb|center|580px|'''Figure 4''': Sketch of the principial structure of the model.]] | ||
| - | First the fluid velocity at the given point is found. The method is the same whether there is 0, 1 or 2 walls, but the tensor used varies. | + | <br>First, the fluid velocity at the given point is found. The method is the same whether there is 0, 1 or 2 walls, but the tensor used varies. <br> |
</p> | </p> | ||
[[Image:Team-SDU-Denmark-Flow.gif|center]] | [[Image:Team-SDU-Denmark-Flow.gif|center]] | ||
<p style="text-align: justify;">The dragforce created by the fluid on the sphere is calculated using the same formula we used in part 3</p> | <p style="text-align: justify;">The dragforce created by the fluid on the sphere is calculated using the same formula we used in part 3</p> | ||
| - | [[Image:Team-SDU-Denmark-2010-Force-2.gif|center]] | + | [[Image:Team-SDU-Denmark-2010-Force-2.gif|center]] <br> |
| - | <p style="text-align: justify;">Once we have the force we can use it to calculate the torque on the sphere, then we summarize the torques of the individual spheres to get the total torque </p> | + | <p style="text-align: justify;">Once we have the force, we can use it to calculate the torque on the sphere, then we summarize the torques of the individual spheres to get the total torque </p> <br> |
[[Image:Team-SDU-Denmark-2010-Torque-2.gif|center]] | [[Image:Team-SDU-Denmark-2010-Torque-2.gif|center]] | ||
| - | <p style="text-align: justify;">We then transformed the torque to angular acceleration by dividing with the inertia. This is also where we introduce the potential, that we mentioned earlier</p> | + | <p style="text-align: justify;"><br>We then transformed the torque to angular acceleration by dividing with the inertia. This is also where we introduce the potential, that we mentioned earlier</p> |
[[Image:Team-SDU-Denmark-2010-Acceleration-2.gif|center]] | [[Image:Team-SDU-Denmark-2010-Acceleration-2.gif|center]] | ||
| - | <p style="text-align: justify;">Now that we have the angular acceleration we can insert it into the equation of motion. This allows us to calculate the position of the flagella at the next timestep by using | + | <p style="text-align: justify;">Now that we have the angular acceleration, we can insert it into the equation of motion. This allows us to calculate the position of the flagella at the next timestep by using its position at the current and at the previous timestep. </p> <br> |
[[Image:Team-SDU-Denmark-2010-Angle-2.gif|center]] | [[Image:Team-SDU-Denmark-2010-Angle-2.gif|center]] | ||
| - | <p style="text-align: justify;">In the end this model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after which the two velocities never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of | + | <p style="text-align: justify;"><br>In the end, this model showed us that in less than 100ns the velocity of the flagella would be the same as the velocity of the fluid when the flagella started with a velocity of zero, after which the two velocities never diverged far from each other. Since the velocity of the flagella always went to the velocity of the fluid on such a short timescale and since these calculations took a lot of computer power we decided that instead of force calculations we would simpy find the flow velocity at the tip of the flagellum and convert that directly to the angular velocity of the flagellum. |
</p> | </p> | ||
| Line 124: | Line 124: | ||
In the following figure we have made many of these runs, but with varying average start-angle </p> | In the following figure we have made many of these runs, but with varying average start-angle </p> | ||
| - | [[Image:Team-SDU-Denmark--2010-start slut.jpeg|center|580px]] | + | [[Image:Team-SDU-Denmark--2010-start slut.jpeg|thumb|center|580px|'''Figure 5''': Shows the mean end angle as a function of the mean start angle, predicted by the 2D model.]] |
<p style="text-align: justify;">As the figure shows a very small deviation in the starting angle will cause a much bigger deviation in the end. The flagella in the systems used for making this graph were all lying down, but to which side the flagella went was highly dependent on the start configuration. When the mean angle was zero corresponding to a vertical flagellum it was pretty much 50-50, but when the start angles were pushed a bit to one side it had a tendency to shift the entire system in that direction. This tells us that if you can control the starting angle, it will go a long way towards creating a uniform flow. | <p style="text-align: justify;">As the figure shows a very small deviation in the starting angle will cause a much bigger deviation in the end. The flagella in the systems used for making this graph were all lying down, but to which side the flagella went was highly dependent on the start configuration. When the mean angle was zero corresponding to a vertical flagellum it was pretty much 50-50, but when the start angles were pushed a bit to one side it had a tendency to shift the entire system in that direction. This tells us that if you can control the starting angle, it will go a long way towards creating a uniform flow. | ||
| Line 133: | Line 133: | ||
The stationary model, does not offer much when it comes to dynamics and interesting behavior, which should not surprise anyone. It does however offer us the opportunity to investigate at which angle the flow in the tube is highest, which could be helpful when planning how to optimize the use of bacteria as a source of flow.</p> | The stationary model, does not offer much when it comes to dynamics and interesting behavior, which should not surprise anyone. It does however offer us the opportunity to investigate at which angle the flow in the tube is highest, which could be helpful when planning how to optimize the use of bacteria as a source of flow.</p> | ||
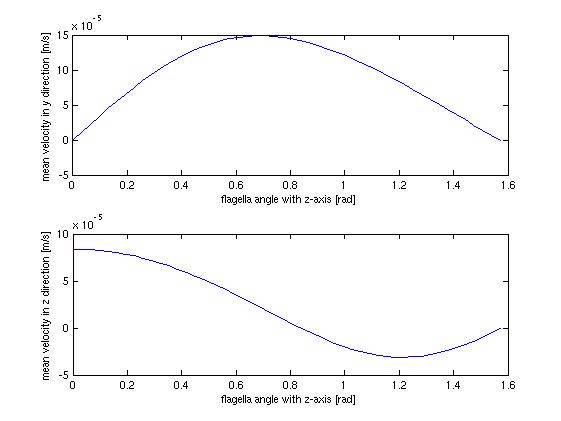
| - | [[Image:Team-SDU-Denmark-hastighed-vinkel-2.jpg|center]] | + | [[Image:Team-SDU-Denmark-hastighed-vinkel-2.jpg|thumb|center|550px|'''Figure 6''': Shows the mean velocity in the z(perpendicular to the surface) and y(parallel to the surface) direction as a function of the flagella agle, pridicted by the static model.]] |
<p style="text-align: justify;">The above figure shows the average flow velocity as a function of the angle of the flagella. In the above case only one wall is taken into account. The one of most importance is the top-one which shows the flow velocity parallel to the tube. According to these figures we get the best velocity at an angle of around 0.7 rad or approximately 40 degrees, where the angle is measured from the axis perpendicular to the wall. | <p style="text-align: justify;">The above figure shows the average flow velocity as a function of the angle of the flagella. In the above case only one wall is taken into account. The one of most importance is the top-one which shows the flow velocity parallel to the tube. According to these figures we get the best velocity at an angle of around 0.7 rad or approximately 40 degrees, where the angle is measured from the axis perpendicular to the wall. | ||
| Line 146: | Line 146: | ||
=====A flagella row on the other wall===== | =====A flagella row on the other wall===== | ||
<p style="text-align: justify;"> | <p style="text-align: justify;"> | ||
| - | In our model we settled for placing bacteria on one wall. During the real-life application, flagella would most likely be placed on both walls. This is not something we have tried to implement in our model, | + | In our model we settled for placing bacteria on one wall. During the real-life application, flagella would most likely be placed on both walls. This is not something we have tried to implement in our model, although doing so should just be a matter of creating an extra grid and adapting the existing model to this. If this was done, it would improve the usability of the model. |
</p> | </p> | ||
| + | |||
===== A better double-wall approximation ===== | ===== A better double-wall approximation ===== | ||
<p style="text-align: justify;"> | <p style="text-align: justify;"> | ||
| Line 155: | Line 156: | ||
=== References === | === References === | ||
<p style="text-align: justify;"> | <p style="text-align: justify;"> | ||
| - | [1] Kim | + | [1] Kim M. J., Breuer K. S., [http://microfluidics.engin.brown.edu/Breuer_Papers/Journals/Small2008_Bacterial_Pump.pdf ''Microfluidic pump powered by self-organizing bacteria''], Small 4, 111-118. (2007) |
<br> | <br> | ||
| - | [2] Berg | + | [2] Berg H. C., [http://www.annualreviews.org/eprint/cDJrS190m62mDRwHrlp9/full/10.1146/annurev.biochem.72.121801.161737 ''The rotary motor of bacterial flagella''], Annu. Rev. Biochem. 72, 19-54. (2003) |
<br> | <br> | ||
| - | [3] Berg | + | [3] Berg H. C., ''E. coli in Motion'', Springer, New York. (2004) |
<br> | <br> | ||
| - | [4] Floresa H, Lobatonb E, Méndez-Diezc S, Tlupovad S, Cortezd R, A study of bacterial flagellar bundling, Bulletin of Mathematical Biology 67 137–168. (2005) | + | [4] Floresa H., Lobatonb E., Méndez-Diezc S., Tlupovad S., Cortezd R., ''A study of bacterial flagellar bundling'', Bulletin of Mathematical Biology 67 137–168. (2005) |
<br> | <br> | ||
| - | [5] Reicherta M, Stark H, Synchronization of rotating helices by hydrodynamic interactions, Eur. Phys. J. E 17, 493-500. (2005) | + | [5] Reicherta M., Stark H., ''Synchronization of rotating helices by hydrodynamic interactions'', Eur. Phys. J. E 17, 493-500. (2005) |
<br> | <br> | ||
| - | [6] Turner L, Ryu | + | [6] Turner L., Ryu W. S., Berg H.C., [http://jb.asm.org/cgi/content/full/182/10/2793?view=long&pmid=10781548 ''Real-Time Imaging of Fluorescent Flagellar Filaments''], JOURNAL OF BACTERIOLOGY, 2793–2801. (2000) |
<br> | <br> | ||
[7] http://commons.wikimedia.org/wiki/File:Flagellum_base_diagram.svg | [7] http://commons.wikimedia.org/wiki/File:Flagellum_base_diagram.svg | ||
<br> | <br> | ||
| - | [8] Uchida N, Golestanian R, Synchronization and Collective Dynamics in A Carpet of Microfluidic Rotors. (2009) | + | [8] Uchida N., Golestanian R., [http://prl.aps.org/abstract/PRL/v104/i17/e178103 ''Synchronization and Collective Dynamics in A Carpet of Microfluidic Rotors''], Phys. Rev. Lett. 104 178103 (2009) |
<br><br> | <br><br> | ||
</p> | </p> | ||
Latest revision as of 20:34, 27 October 2010
 "
"