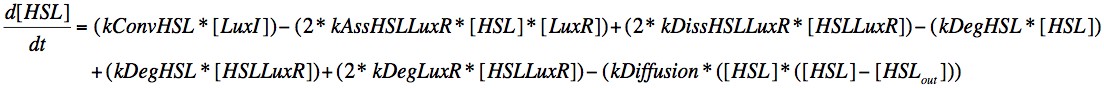Team:St Andrews/project/modelling/model 2
From 2010.igem.org
(→Theory & assumptions) |
|||
| Line 20: | Line 20: | ||
'''Figure 2: Graph of GFP concentration against time''' | '''Figure 2: Graph of GFP concentration against time''' | ||
| + | |||
| + | |||
| + | [[Image:LuxRSingleCellLoopRampUpLarge.jpg|800px]] | ||
| + | |||
| + | |||
| + | '''Figure 3: Graph of GFP, LuxI and LuxR concentrations against time''' | ||
Revision as of 15:59, 7 September 2010


Model 2: Single Cell With Loop
Theory & assumptions
Our second model introduced the concept of an external environment into which the HSL could diffuse into. This was assumed to be of infinite volume and thus the concentration of HSL in this region would always be zero, regardless of the quantity of HSL leaving the cell. In order to implement this modification we produced a new differential to desrcibe the change in HSL.
The creation of HSL is dictated by kConv, which is associated with the ability of LuxI to catalyse the conversion of resources into HSL. The concentration is reduced by the association with LuxR and by natural degredation. It is also affected by the degredation of molecules in the HSL-LuxR complex in the same way that LuxR is. We also introduce a diffusion term which accounts for HSL diffusing out of the cell due to a concentration gradient between the cell and the external environment.
Results
The switching on behaviour produced by this model is shown in figure . This switching on can be interpreted as the cell turning itself on due to the HSL it produces not diffusing out of the cell at a high enough rate. Therefore there is a considerable concentration of HSL remaining in the cell to maintain the feedback loop and produce more HSL. Thus regardless of the initial concentrations our cell always switches on. This does not match with the true biological scenario at all. Quorum sensing is designed such that cells will only become up-regulated when present at a certain critical cell density. Therefore the suggestion made by our results that a single cell can self-activate undermines this principle entirely.
Figure 2: Graph of GFP concentration against time
Figure 3: Graph of GFP, LuxI and LuxR concentrations against time
 "
"