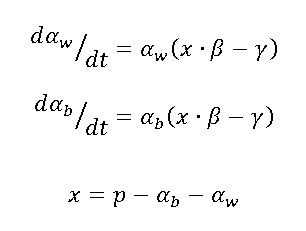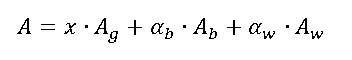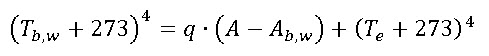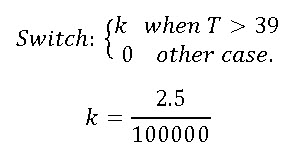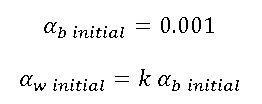Team:Valencia/Modeling
From 2010.igem.org
(→Yeastworld Mathematics) |
Alejovigno (Talk | contribs) (→Yeastworld Mathematics) |
||
| (18 intermediate revisions not shown) | |||
| Line 47: | Line 47: | ||
It is important to keep in mind that the black and white yeasts and the Yeastworld background albedo are different and that this fact is the key concept that allows the process to work. For checking the differences in albedo and temperature in the different color cultures check the [[Team:Valencia/WB | Microbial Albedo Recorder ]] section. | It is important to keep in mind that the black and white yeasts and the Yeastworld background albedo are different and that this fact is the key concept that allows the process to work. For checking the differences in albedo and temperature in the different color cultures check the [[Team:Valencia/WB | Microbial Albedo Recorder ]] section. | ||
| + | </div> | ||
| + | <div id="HomeCenterB"> | ||
| + | <div style="margin-top: 8px; margin-bottom: 20px; margin-left: 12px; margin-right: 12px;"> | ||
=== Yeastworld Mathematics === | === Yeastworld Mathematics === | ||
The mathematical model for Yeastworld is not really that much complex. The system is represented by the following group of equations | The mathematical model for Yeastworld is not really that much complex. The system is represented by the following group of equations | ||
| - | [[Image:Valencia_model_eq1.jpg|center | + | [[Image:Valencia_model_eq1.jpg|center||]] |
α<sub>w</sub> and α<sub>b</sub> represent the surface of the planet cover by white and black yeasts | α<sub>w</sub> and α<sub>b</sub> represent the surface of the planet cover by white and black yeasts | ||
| + | |||
x is the uncolonized fertile ground of Yeastworld | x is the uncolonized fertile ground of Yeastworld | ||
| + | |||
p is the global surface of the planet | p is the global surface of the planet | ||
| - | β is the mathematical function that represents the yeast growth depending on the temperature | + | |
| + | β is the mathematical function that represents the yeast growth depending on the temperature with a maximum value at 30ºC. | ||
γ = 0.3 is a constant death rate of the yeasts | γ = 0.3 is a constant death rate of the yeasts | ||
| + | |||
Those first equations represent the evolution of the areas of each kind of yeast over time. The following equation is known as the Stefan Boltzmann equation and relates the temperature of the planet with the albedo and the solar luminosity that arrives to Yeastworld. | Those first equations represent the evolution of the areas of each kind of yeast over time. The following equation is known as the Stefan Boltzmann equation and relates the temperature of the planet with the albedo and the solar luminosity that arrives to Yeastworld. | ||
| - | [[Image:Valencia_model_eq2.jpg|center | + | [[Image:Valencia_model_eq2.jpg|center||]] |
σ is the Stefan equation | σ is the Stefan equation | ||
| + | |||
SL is the luminosity coming from the Sun and arriving to Yeastworld | SL is the luminosity coming from the Sun and arriving to Yeastworld | ||
| - | |||
| + | A is the global albedo of the Yeastworld. | ||
| - | + | The next equation relates the global albedo with the albedo of the surfaces covered by the two kind of yeasts. | |
| + | [[Image:Valencia_model_eq3.jpg|center||]] | ||
A<sub>g</sub> = 0.6 is the albedo of the free surface of the planet | A<sub>g</sub> = 0.6 is the albedo of the free surface of the planet | ||
| + | |||
A<sub>b</sub> = 0.3 is the albedo of the black yeasts | A<sub>b</sub> = 0.3 is the albedo of the black yeasts | ||
| + | |||
A<sub>w</sub> = 0.75 is the albedo of the white yeasts | A<sub>w</sub> = 0.75 is the albedo of the white yeasts | ||
| + | |||
And finally this last equation relates the temperature of the cultures with the global albedo and the global temperature of Yeastworld. | And finally this last equation relates the temperature of the cultures with the global albedo and the global temperature of Yeastworld. | ||
| - | + | [[Image:Valencia_model_eq4.jpg|center||]] | |
| - | [[Image:Valencia_model_eq4.jpg|center | + | |
T<sub>b,w</sub> is the temperature of the black or white yeasts | T<sub>b,w</sub> is the temperature of the black or white yeasts | ||
| + | |||
A<sub>b,w</sub> is the albedo of each surface of the yeasts (white or black) | A<sub>b,w</sub> is the albedo of each surface of the yeasts (white or black) | ||
We also incorporated a simplification of the prion infection dynamics, as appears in the next equation, when the temperature of the black yeasts reaches a value near the heat shock (39ºC), the switch turns ON, then there is a fraction of the black area that switches to white. A probable value for this fraction k was taken from (Tyedmers et all, 2008) | We also incorporated a simplification of the prion infection dynamics, as appears in the next equation, when the temperature of the black yeasts reaches a value near the heat shock (39ºC), the switch turns ON, then there is a fraction of the black area that switches to white. A probable value for this fraction k was taken from (Tyedmers et all, 2008) | ||
| - | [[Image:Valencia_model_eq5.jpg|center | + | [[Image:Valencia_model_eq5.jpg|center||]] |
Then, we developed a software tool designed with MatLab in order to integrate of the equations together and make the model working. In addition of all data shown above we had to establish a starting situation: | Then, we developed a software tool designed with MatLab in order to integrate of the equations together and make the model working. In addition of all data shown above we had to establish a starting situation: | ||
| - | [[Image:Valencia_model_eq6.jpg|center | + | [[Image:Valencia_model_eq6.jpg|center||]] |
This situation is an approximation of the real starting terraforming process where the area covered by black yeast is very low and the white yeasts one is even much smaller. Since the temperature at the beginning is quite low no white yeast would appear until the [[:Team:Valencia/prion#Behaviour | prionic switch ]] turned on. | This situation is an approximation of the real starting terraforming process where the area covered by black yeast is very low and the white yeasts one is even much smaller. Since the temperature at the beginning is quite low no white yeast would appear until the [[:Team:Valencia/prion#Behaviour | prionic switch ]] turned on. | ||
| Line 93: | Line 105: | ||
We had to assume a very low initial amount of white yeasts in order to make the model work. The coefficient k that relates αw and αb is related with the frequency of switching from black to white. | We had to assume a very low initial amount of white yeasts in order to make the model work. The coefficient k that relates αw and αb is related with the frequency of switching from black to white. | ||
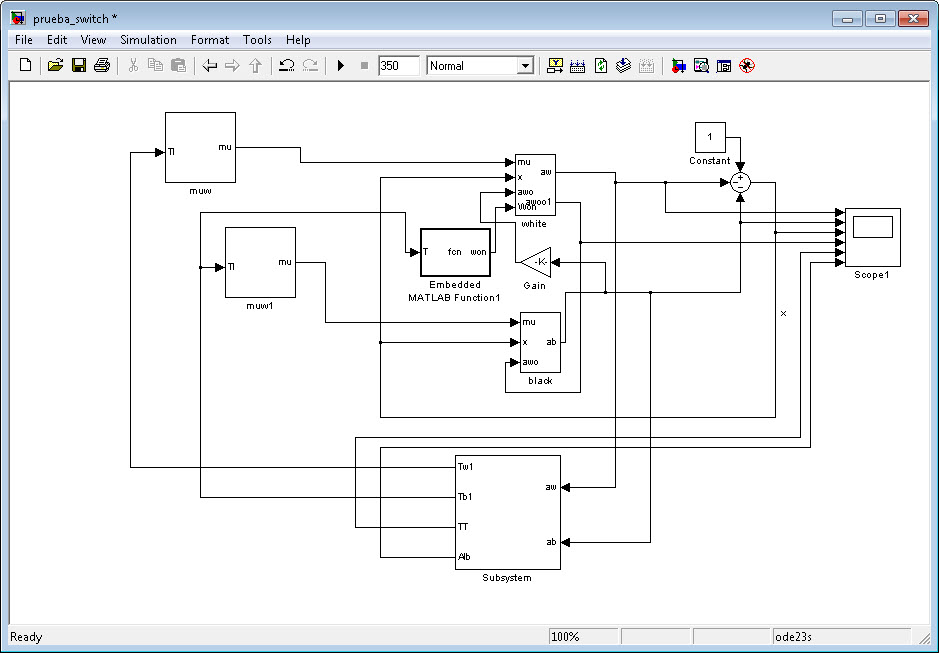
This picture shows the kernel of the MatLab programme that runs the model. | This picture shows the kernel of the MatLab programme that runs the model. | ||
| + | |||
| + | [[Image:Valencia_model_ss.jpg|center|675px|Yeastworld in Simulink.]] | ||
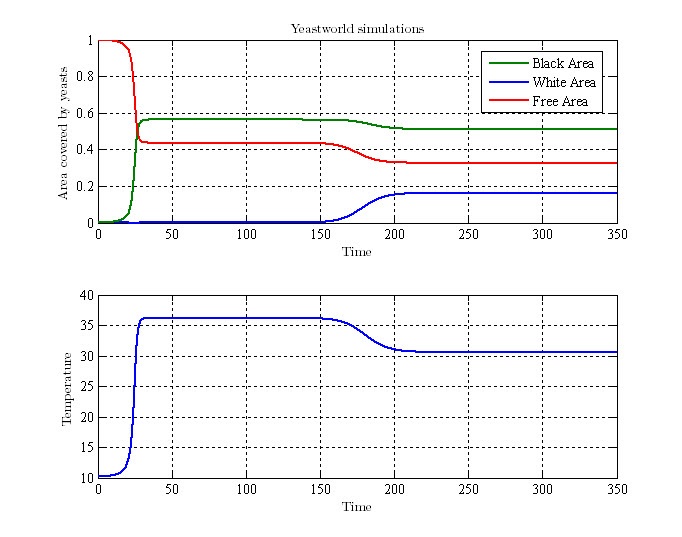
Our Yeastworld model simulates the running of the system through the following graphs: | Our Yeastworld model simulates the running of the system through the following graphs: | ||
| - | [[Image: | + | [[Image:Valencia_model_result1.jpg|center|500px|Yeastworld evolution of yeasts areas.]] |
In the first graph we can observe the areas of black yeasts, white yeasts and background. In the second graph it is possible to visualize the evolution of the temperature in the simulation. You can realize very easily that as the area of black yeasts spreads the temperature increases. Later on, when the temperature reaches a certain point, the switch turns on and activates the generation and spreading of white yeasts. These white and black yeasts reach eventually a steady state that modulates and finally keeps the temperature constant. | In the first graph we can observe the areas of black yeasts, white yeasts and background. In the second graph it is possible to visualize the evolution of the temperature in the simulation. You can realize very easily that as the area of black yeasts spreads the temperature increases. Later on, when the temperature reaches a certain point, the switch turns on and activates the generation and spreading of white yeasts. These white and black yeasts reach eventually a steady state that modulates and finally keeps the temperature constant. | ||
| + | |||
It is possible to look at the model from the albedo perspective. Then the albedo stabilizes and later increases a bit when the switch turns on and the steady state is reached. | It is possible to look at the model from the albedo perspective. Then the albedo stabilizes and later increases a bit when the switch turns on and the steady state is reached. | ||
| - | [[Image: | + | [[Image:Valencia_model_result2.jpg|center|500px|Yeastworld temperature variation due to albedo control.]] |
The albedo evolution is quite related with the temperature one. First the albedo decreases very fast as the black yeasts spread. | The albedo evolution is quite related with the temperature one. First the albedo decreases very fast as the black yeasts spread. | ||
| Line 108: | Line 123: | ||
'''References''' | '''References''' | ||
| - | Lovelock, J. E. and Watson, A. J. (1983). Biological homeostasis of global environment: the parable of Daisyworld. ``Tellus´´. 35B, 284-289. | + | *Lovelock, J. E. and Watson, A. J. (1983). Biological homeostasis of global environment: the parable of Daisyworld. ``Tellus´´. 35B, 284-289. |
| - | Tyedmers, J. Madariaga, M. L. Lindquist, S. (2008). Prion switching in reponse to environmental stress. ``PLoS Biology´´. 6: e294. | + | |
| + | *Tyedmers, J. Madariaga, M. L. Lindquist, S. (2008). Prion switching in reponse to environmental stress. ``PLoS Biology´´. 6: e294. | ||
</div> | </div> | ||
Latest revision as of 15:51, 9 February 2011
Time goes by...
(El tiempo pasa...)
Follow us:

Our main sponsors:

Our institutions:

Visitor location:
» Home
Mathematical Modeling
Modeling Mad Yeast On Mars
Introduction
The real system we want to model is formed by three basic but different elements:
- Physical element: Mars, the planet we want to terraform. It is defined by a series of physical parameters. Mars is the environment, the frame in which the terraforming takes place.
- Biological element: Saccharomices cereviseae, the yeast we used as chassis or vector to colonize the planet. The yeasts are the vector, the way it has been used to achieve this terraforming goal.
- Molecular element: prionic circuit that works as a switch between yeasts that express different proteins. The prionic switch is the key mechanism that allows the terraforming process itself.
A model is not just a tool that science and engineering use to allow us to understand the reality that surrounds us. Moreover, it helps us to explain and predict the physical principles of universe we live in. Modeling is by definition simplifying. We use simply it because it is useful.
There are some climate models that intend to explain the global physical characteristics of Mars. These kinds of models are extremely complex. Hundreds of different variables are connected by equations and networks. Honestly, they are far beyond any iGEM team could achieve with some months of working. It is simply too complex. In fact, they are not really efficient in predicting anything, not even the ones on Earth. Global climate is something still too complex to be represented in a model with a minimum of confidence.
Therefore, what did we do? Well the answer is not really so difficult. We focused primarily in the very definition of the term model. This way, we develop a group of mathematical equations that allow us (and more important, you!) to understand how this hypothetical terraforming process would eventually move on. We used as inspiration a model known as Daisyworld developed by Watson and Lovelock (1983) for other totally different purpose, which was to support the Lovelock Gaia Hypothesis. Daisyworld is a static (mind this!) and very simple model of a planet which is able to regulate its own temperature using the living organisms living in it, in this case, daisies. We named our model in a similar way to pay tribute to that excellent piece of work.
Welcome to the Yeastworld: theoretical background
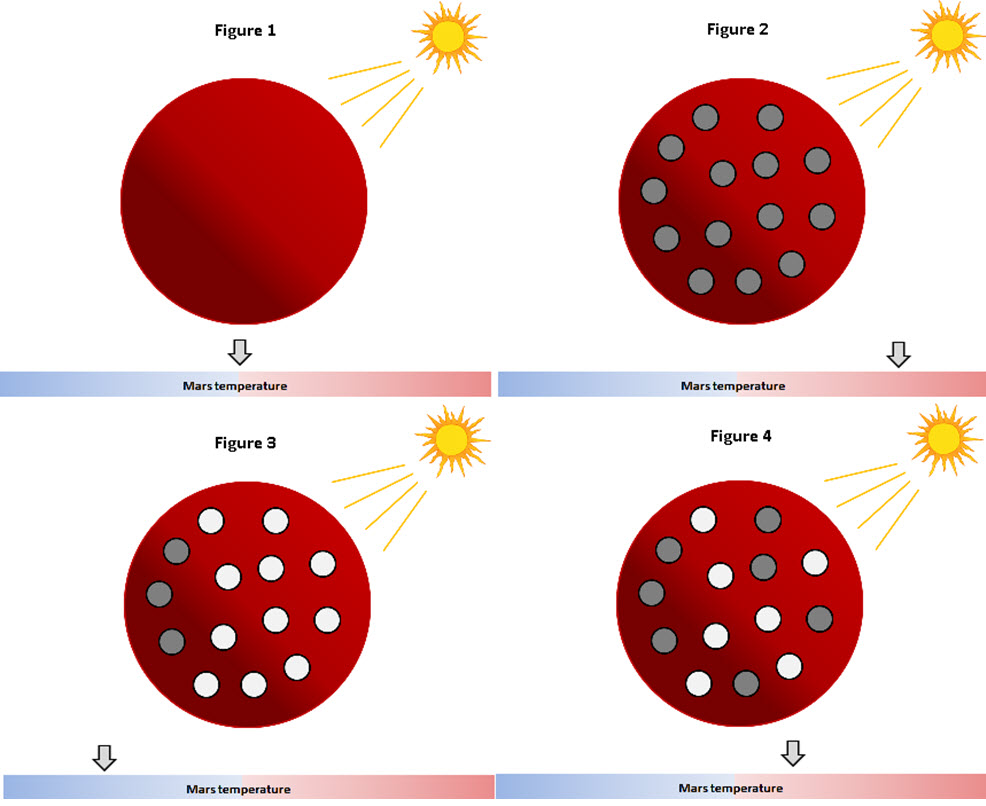
Yeastworld is a simplistic version of Mars. Some input parameters of the model derive from the real values on Mars: solar luminosity, distance from the Sun, lack of atmosphere, initial temperature and background albedo. At the beginning in the Yeastworld there is no life at all (Figure 1).
Then, black pigmented yeasts (or [psi-] yeasts) appear thanks to human action. These black yeasts are able to grow under the medium-low temperatures that mimic the conditions of a partially terraformed Mars. As they start to spread, they progressively expand and cover an important portion of the planet surface. Due to the albedo effect reduction (see Microbial Albedo Recorder for more details), the entire planet starts to warm up (Figure 2).
As we explained in the prionic switch section, even in this conditions some white ([PSI+]) colonies will appear. However, their presence will become relevant as the temperature increases. The prion-based switch allows the change from black to white yeast by stopping the pigment expression. Together with this molecular underlying process, the [PSI+] yeasts will be selected in favour in these warm conditions. This is due to their intrinsic protection against overheating and their ability to reduce the local temperature. Therefore, the white yeasts will finally cover a big portion of the Yeastworld surface. This will importantly increase the albedo effect of the planet and reduce the global temperature (Figure 3).
In this situation, the opposite process will take place. At low temperatures the black yeasts will have a higher growing rate because of the elevated inner temperature at which their cellular processes will take place, so they will again displace the white cells. Together with the fact that the prion activation will not be highly promoted, this will result in a major abundance of the black [psi-] yeasts, thus increasing again the temperature.
This cycle of white and black yeasts goes on and on and finally ends in a steady state (Figure 4) in which the amount of each kind of yeast is constant and so it is the global temperature (and albedo). Therefore, we can regulate the Yeastworld temperature by using our engineered yeasts. This capability of regulate the temperature of an entire planet is one of the most important points of our proposal of Terraforming process.
It is also interesting to remember that our yeasts could express LEA protein aswell so their resistance to extreme temperatures is improved. Moreover, note that the key parameter studied and modeled here is not the temperature but the albedo. The temperature is only the physical consequence that arises from modifying the albedo of the planet.
It is important to keep in mind that the black and white yeasts and the Yeastworld background albedo are different and that this fact is the key concept that allows the process to work. For checking the differences in albedo and temperature in the different color cultures check the Microbial Albedo Recorder section.
Yeastworld Mathematics
The mathematical model for Yeastworld is not really that much complex. The system is represented by the following group of equations
αw and αb represent the surface of the planet cover by white and black yeasts
x is the uncolonized fertile ground of Yeastworld
p is the global surface of the planet
β is the mathematical function that represents the yeast growth depending on the temperature with a maximum value at 30ºC.
γ = 0.3 is a constant death rate of the yeasts
Those first equations represent the evolution of the areas of each kind of yeast over time. The following equation is known as the Stefan Boltzmann equation and relates the temperature of the planet with the albedo and the solar luminosity that arrives to Yeastworld.
σ is the Stefan equation
SL is the luminosity coming from the Sun and arriving to Yeastworld
A is the global albedo of the Yeastworld.
The next equation relates the global albedo with the albedo of the surfaces covered by the two kind of yeasts.
Ag = 0.6 is the albedo of the free surface of the planet
Ab = 0.3 is the albedo of the black yeasts
Aw = 0.75 is the albedo of the white yeasts
And finally this last equation relates the temperature of the cultures with the global albedo and the global temperature of Yeastworld.
Tb,w is the temperature of the black or white yeasts
Ab,w is the albedo of each surface of the yeasts (white or black)
We also incorporated a simplification of the prion infection dynamics, as appears in the next equation, when the temperature of the black yeasts reaches a value near the heat shock (39ºC), the switch turns ON, then there is a fraction of the black area that switches to white. A probable value for this fraction k was taken from (Tyedmers et all, 2008)
Then, we developed a software tool designed with MatLab in order to integrate of the equations together and make the model working. In addition of all data shown above we had to establish a starting situation:
This situation is an approximation of the real starting terraforming process where the area covered by black yeast is very low and the white yeasts one is even much smaller. Since the temperature at the beginning is quite low no white yeast would appear until the prionic switch turned on.
We had to assume a very low initial amount of white yeasts in order to make the model work. The coefficient k that relates αw and αb is related with the frequency of switching from black to white. This picture shows the kernel of the MatLab programme that runs the model.
Our Yeastworld model simulates the running of the system through the following graphs:
In the first graph we can observe the areas of black yeasts, white yeasts and background. In the second graph it is possible to visualize the evolution of the temperature in the simulation. You can realize very easily that as the area of black yeasts spreads the temperature increases. Later on, when the temperature reaches a certain point, the switch turns on and activates the generation and spreading of white yeasts. These white and black yeasts reach eventually a steady state that modulates and finally keeps the temperature constant.
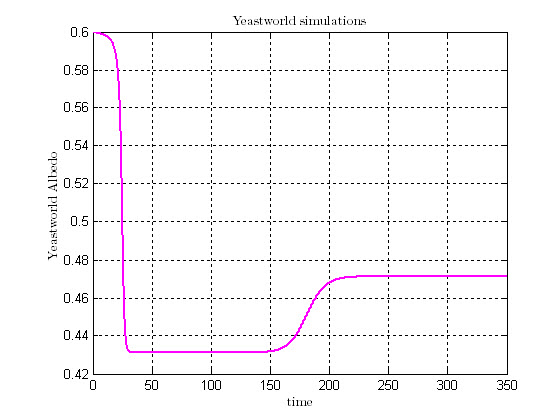
It is possible to look at the model from the albedo perspective. Then the albedo stabilizes and later increases a bit when the switch turns on and the steady state is reached.
The albedo evolution is quite related with the temperature one. First the albedo decreases very fast as the black yeasts spread. In short, Yeastworld is a simple model to simulate and represent the process of terraforming that we proposed.
References
- Lovelock, J. E. and Watson, A. J. (1983). Biological homeostasis of global environment: the parable of Daisyworld. ``Tellus´´. 35B, 284-289.
- Tyedmers, J. Madariaga, M. L. Lindquist, S. (2008). Prion switching in reponse to environmental stress. ``PLoS Biology´´. 6: e294.
 "
"