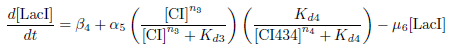Team:Brown/Modeling/ODEs
From 2010.igem.org
| Line 2: | Line 2: | ||
==ODE Modeling of the Quad-State circuit== | ==ODE Modeling of the Quad-State circuit== | ||
| - | |||
| - | |||
We formulated a system of differential equations which we used to model our system. As we have many players in our system and thus many equations, we chose to combine transcription and translation into single equations representing protein synthesis. | We formulated a system of differential equations which we used to model our system. As we have many players in our system and thus many equations, we chose to combine transcription and translation into single equations representing protein synthesis. | ||
| Line 18: | Line 16: | ||
We chose to simplify our model by expressing simultaneous repression/induction as the product of the corresponding hill equations. This is a simplification because it allows both the repressor and inducer to bind simultaneously, while in reality they are competing for available space. | We chose to simplify our model by expressing simultaneous repression/induction as the product of the corresponding hill equations. This is a simplification because it allows both the repressor and inducer to bind simultaneously, while in reality they are competing for available space. | ||
| + | __TOC__ | ||
=== Production of LovTAP === | === Production of LovTAP === | ||
Revision as of 07:46, 25 October 2010
ODE Modeling of the Quad-State circuit
We formulated a system of differential equations which we used to model our system. As we have many players in our system and thus many equations, we chose to combine transcription and translation into single equations representing protein synthesis.
In all cases the equations represent the change in concentration in nanomoles/minute. Most equations make use of the Hill equation, which is used to model the cooperative binding of a ligand to a molecule. This is accomplished by describing the fraction of bound macromolecule as a function of ligand concentration.
We model induction by ligand X as: 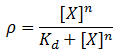
We model repression by ligand X as: 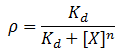
Where rho is the fraction of occupied ligand binding sites, [X] is the ligand concentration, n is the hill coefficient, and K_d is the equilibrium constant for dissociation.
We chose to simplify our model by expressing simultaneous repression/induction as the product of the corresponding hill equations. This is a simplification because it allows both the repressor and inducer to bind simultaneously, while in reality they are competing for available space.
Production of LovTAP
Biological Process
This equation represents the rate of change of the (light-) LovTAP protein concentration over time. LovTAP is under the pTAC promoter/operator. pTAC is a strong hybrid promoter; its expression is repressed by lacI, and the addition of IPTG inactivates the lacI repressor. In this equation, we assume constant induction of pTAC and thus a constant production of LovTAP.
The concentration of LovTAP will be decreased both by conformational change to (light+) LovTAP*, as well as through degradation of the protein.
Differential Equation
Production of LovTAP*
Biological Process
This equation represents the rate of change in LovTAP* (light+) protein over time. The concentration of LovTAP* increases when LovTAP undergoes light-induced conformational change into LovTAP*
The concentration of LovTAP* will be decreased through degradation. We assume that LovTAP* does not change conformation back to LovTAP.
Differential Equation
Production of tetR
Biological Process
This equation represents the rate of change of tetR protein concentration over time. The tetR transcription factor is controlled by the constitutive TrpR promoter, which is repressed by LovTAP*. Thus, [tetR] is inversely correlated to [LovTAP*].
The concentration of tetR is decreased through protein degradation.
Differential Equation
Production of Mnt
Biological Process
This equation represents the rate of change of Mnt protein concentration over time. Mnt is under control of the p(tetR) repressible promoter.
The concentration of Mnt is decreased through protein degradation.
Differential Equation
Production of AraC
Biological Process
This equation represents the rate of change of AraC protein concentration over time. AraC is under control of the p(tetR) repressible promoter.
The concentration of AraC is decreased through protein degradation.
Differential Equation
Production of LacI
Biological Process
This equation represents the rate of change of the LacI protein concentration over time. LacI is under the control of the PRM promoter, which is induced by CI and repressed by CI434.
The concentration of LacI is decreased through protein degradation.
Differential Equation
Production of CI
Biological Process
This equation represents the rate of change of the CI protein over time. CI is produced both by the PRM promoter, as well as the p(tetR) promoter. Consequently, CI is formed when tetR is absent, CI434 is absent, and when CI is present.
The concentration of CI decreases through protein degradation.
Differential Equation
Production of CI434
Biological Process
This equation represents the rate of change of the CI434 protein over time. CI434 is under the control of the PR promoter, which is repressed by CI. CI434 is also produced by the AND gate under pT7.
The concentration of CI434 decreases through protein degradation.
Differential Equation
Production of SupD
Biological Process
This equation represents the rate of change of the SupD protein over time. SupD is a part of our AND gate, and is under the control of the UAS promoter, which is induced by GAL4.
The concentration of SupD decreases through protein degradation, as well as through combination with T7ptag to form T7 polymerase. We assume that the reaction SupD + T7ptag --> T7 Polymerase is rate limited by the concentration of the minimal reactant.
Differential Equation
Production of T7ptag
Biological Process
This equation represents the rate of change of the T7ptag protein over time. T7ptag is a part of our AND gate, and is under the control of the pBad promoter, which is induced by AraC.
The concentration of T7ptag decreases through protein degradation, as well as through combination with SupD to form T7 polymerase. Again, we assume that the reaction SupD + T7ptag --> T7 Polymerase is rate limited by the concentration of the minimal reactant.
Differential Equation
Production of T7 Polymerase
Biological Process
This equation represents the rate of change of the T7 polymerase over time. T7 polymerase is the result of the activation of the AND gate, and is formed through the combination of SupD and T7ptag.
The concentration of T7 polymerase decreases over time due to degradation.
Differential Equation
Production of GAL4
Biological Process
This equation represents the rate of change of GAL4 over time. GAL4 is under the control of pT7, as well as the LacI/Mnt hybrid promoter. Thus, GAL4 is induced by the presence of LacI + IPTG, as well as by T7 polymerase.
The concentration of GAL4 decreases due to protein degradation.
Differential Equation
Production of S1
Biological Process
The equation represents the rate of change of S1 protein over time. S1 is a signaling protein, and indicates that the circuit is in the first state. S1 can be a fluorescent protein, but it can also be a transcription factor that triggers a cascade of regulatory effects. The production of S1 is repressed by CI.
Concentration of the S1 protein decreases over time due to degradation.
Differential Equation
Production of S2
Biological Process
The equation represents the rate of change of S2 protein over time. S2 is a signaling protein, and indicates that the circuit is in the second state. The production of S2 is induced by CI and repressed by CI434.
Concentration of the S2 protein decreases over time due to degradation.
Differential Equation
Production of S3
Biological Process
The equation represents the rate of change of S3 protein over time. S3 is a signaling protein, and indicates that the circuit is in the third state. S3 is induced by LacI (and IPTG, which is assumed to be present) and repressed by Mnt.
Concentration of the S3 protein decreases over time due to degradation.
Differential Equation
Production of S4
Biological Process
The equation represents the rate of change of S4 protein over time. S4 is a signaling protein, and indicates that the circuit is in the fourth state. S4 is formed by T7 polymerase.
Concentration of the S4 protein decreases over time due to degradation.
 "
"