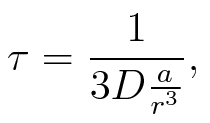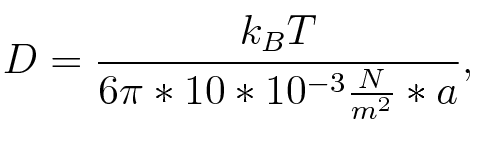Team:TU Munich/Modeling
From 2010.igem.org
(→Overview) |
(→Diffusion) |
||
| Line 31: | Line 31: | ||
<br> | <br> | ||
| - | where ''D'' is the diffusion constant, ''a'' the radius of gyration of the signal molecule and ''r'' the radius of the | + | where ''D'' is the diffusion constant, ''a'' the radius of gyration of the signal molecule and ''r'' the radius of the compartment.<br> |
| - | For ''E. coli'' ''r'' is 1 μm. The radius of gyration ''a'' can be estimated using the worm-like-chain model by <br> | + | For ''E. coli'' ''r'' is approximately 1 μm. The radius of gyration ''a'' can be estimated using the worm-like-chain [TODO: add citation] model by <br> |
[[Image:TU_Munich_iGEM2010_sstraub_a.png |center|100 px]] | [[Image:TU_Munich_iGEM2010_sstraub_a.png |center|100 px]] | ||
| Line 45: | Line 45: | ||
where ''k<sub>B</sub>'' is the Boltzmann constant and ''T'' is the absolute temperature. <br> | where ''k<sub>B</sub>'' is the Boltzmann constant and ''T'' is the absolute temperature. <br> | ||
| - | Using the ''a'' we calculated above, we get D = 3,4318 m<sup>2</sup>/s. <br> | + | Using the ''a'' we calculated above and T = TODO K, we get D = 3,4318 m<sup>2</sup>/s. <br> |
| - | Thus, for a cell containing 100 signal molecules, the signal needs '''0,1518 sec''' until it first hits the terminator sequence. | + | Thus, for a cell containing 100 signal molecules, the signal needs approximately '''0,1518 sec''' until it first hits the terminator sequence. |
{{:Team:TU Munich/Templates/ToggleBoxEnd}} | {{:Team:TU Munich/Templates/ToggleBoxEnd}} | ||
===Results=== | ===Results=== | ||
| - | As the folding time (at least 1,7 sec for full signal length) is significantly larger than the estimated diffusion time (0,1518 sec), diffusion does not play an important role and thus can be neglected in the modeling our signal-terminator constructs. | + | As the folding time (at least '''1,7 sec''' for full signal length) is significantly larger than the estimated diffusion time ('''0,1518 sec'''), diffusion does not play an important role and thus can be neglected in the modeling our signal-terminator constructs. |
=Switch= | =Switch= | ||
Revision as of 12:59, 27 October 2010
|
||||||||||||||||||||
|
|
OverviewWe investigated our signal-terminator construct (toggle switch) with mathematically in two steps: 1) finding of signal and the terminator, 2) signal-terminator binding dynamics. We simulated the termination and antitermination properties of our signal-terminator constructs with the Kinefold web server[1] and used some standard estimations for diffusive terms. Our main goal was to prove that our constructs work and that termination is stopped efficiently, that is, that the signal molecule binds and antiterminations occurs before the RNA polymerase falls off. Diffusion [TODO] ResultsOur estimations showed that diffusion can be neglected and our RNA dynamics simulations showed for each terminator that for appropriate signal length the terminator is not folding, hence antitermination is successful. We also found that much smaller signal length is suitable for antitermination. Finally, we showed using the example of an AND gate that logic gates based on our signal-terminator constructs work well. DiffusionThe question whether antitermination occurs is not only guided by the folding process of the signal-terminator pair, but also by how long the signal takes to diffuse to the terminator sequence.
To account for the diffusion time, we estimated the hit rate τ[2], which is the time until the signal meets the terminator sequence for the first time:
where D is the diffusion constant, a the radius of gyration of the signal molecule and r the radius of the compartment.
where n is the length of the signal which is 0,3 nm/monomer, l is the persistency length[3] which is 2nm for single-stranded RNA. Thus, for a signal of length 32 nt, a = 6,4 nm. The diffusion constant D was obtained by
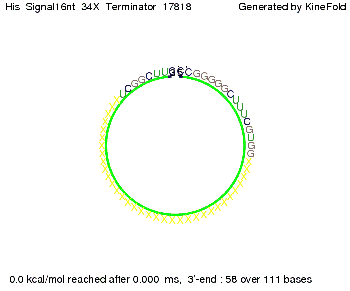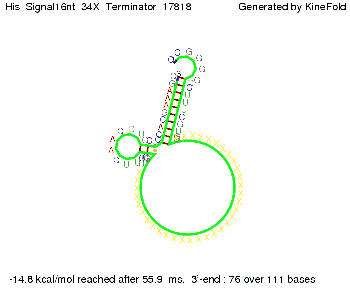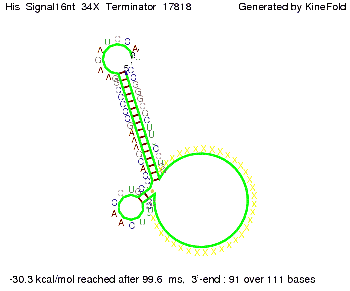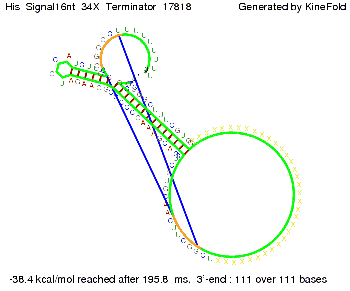
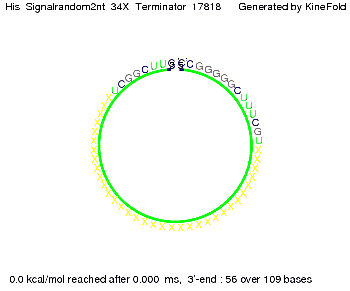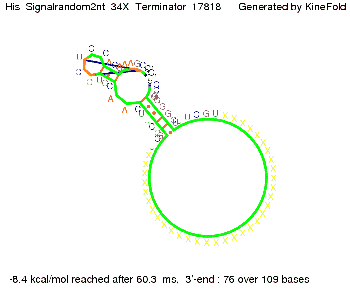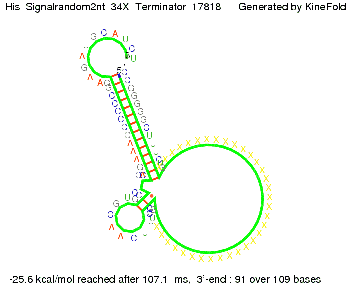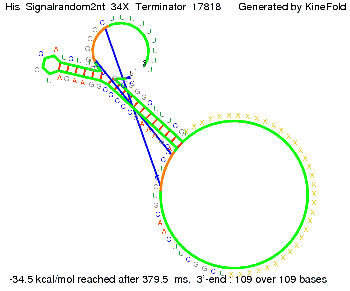
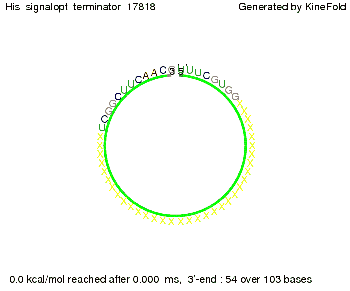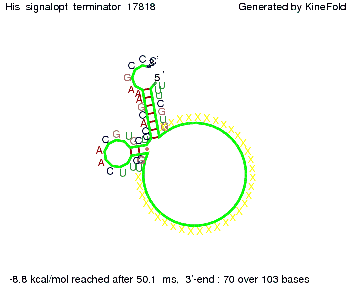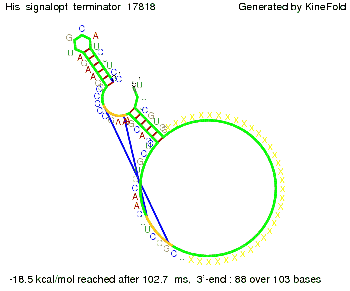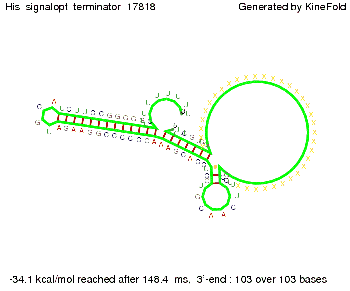
where kB is the Boltzmann constant and T is the absolute temperature. Thus, for a cell containing 100 signal molecules, the signal needs approximately 0,1518 sec until it first hits the terminator sequence. CloseResultsAs the folding time (at least 1,7 sec for full signal length) is significantly larger than the estimated diffusion time (0,1518 sec), diffusion does not play an important role and thus can be neglected in the modeling our signal-terminator constructs. SwitchWe performed Kinefold simulations for the His-terminator, the Trp-terminator and for the T7-terminator, each with the corresponding signal. For each terminator-signal construct there are folding path videos available below and we also optimized the signal sequences. We find that all our toogle switch works well with all three terminators. I. His-terminatorTerminator sequence: Both terminator and signal sequence comprise two parts:
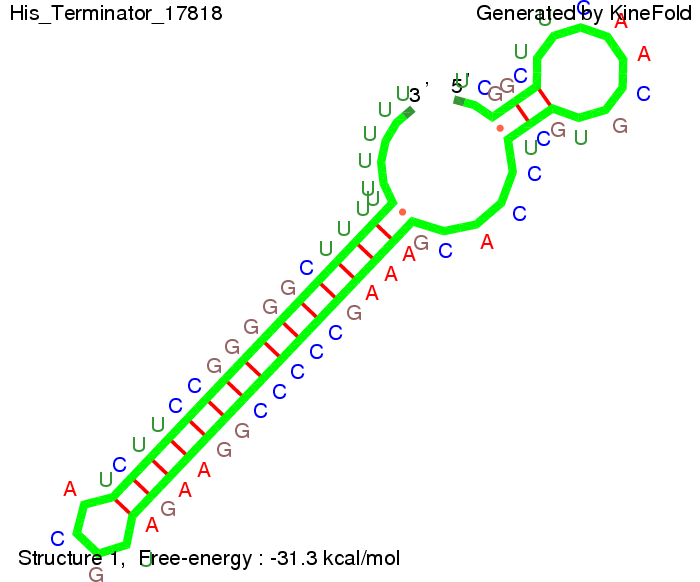
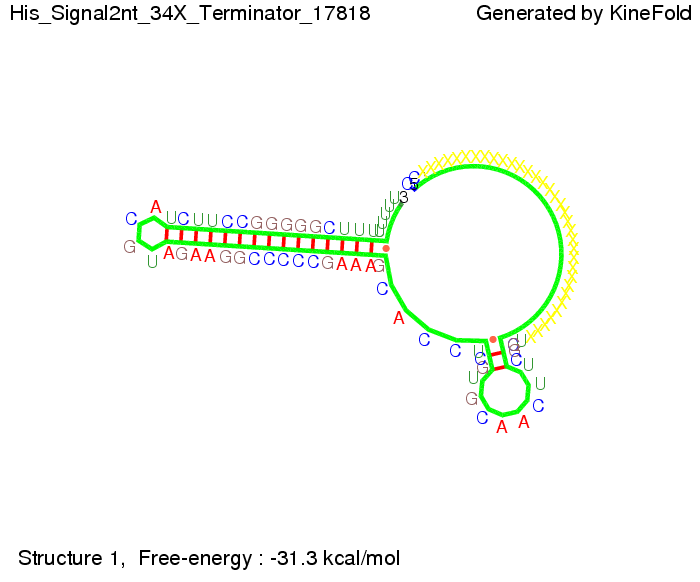
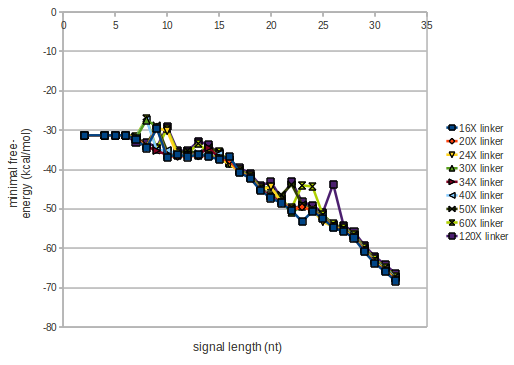
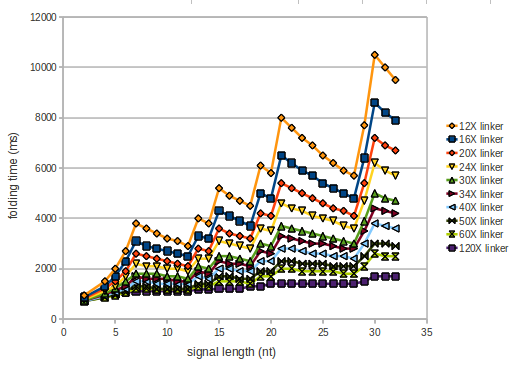
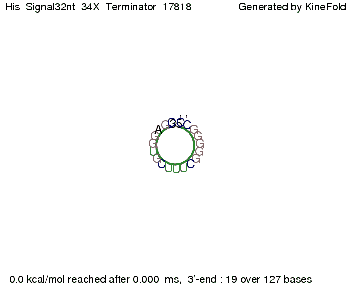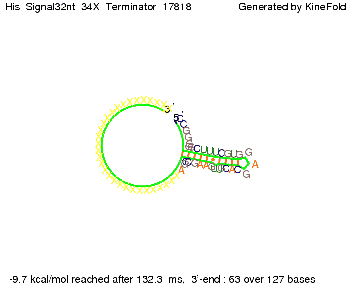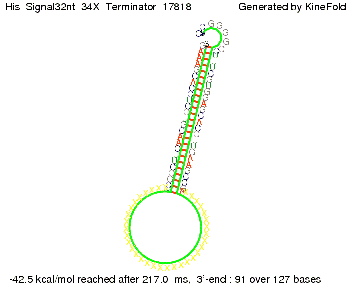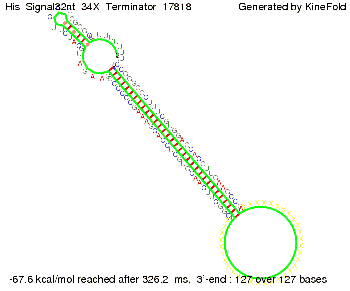
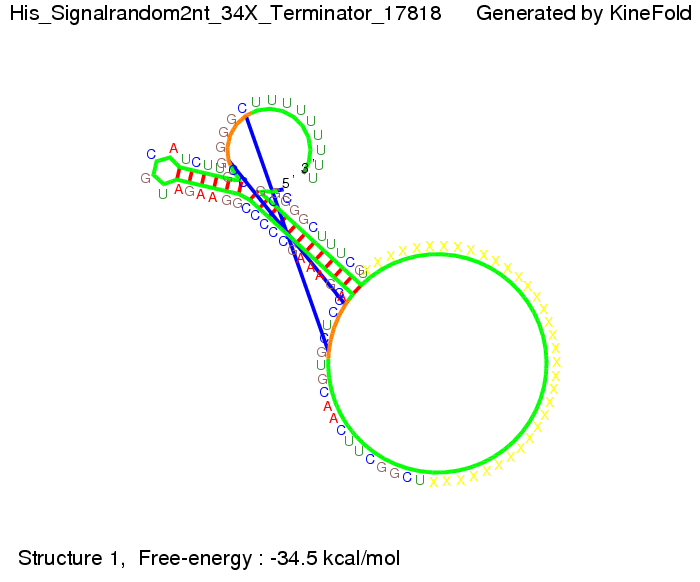
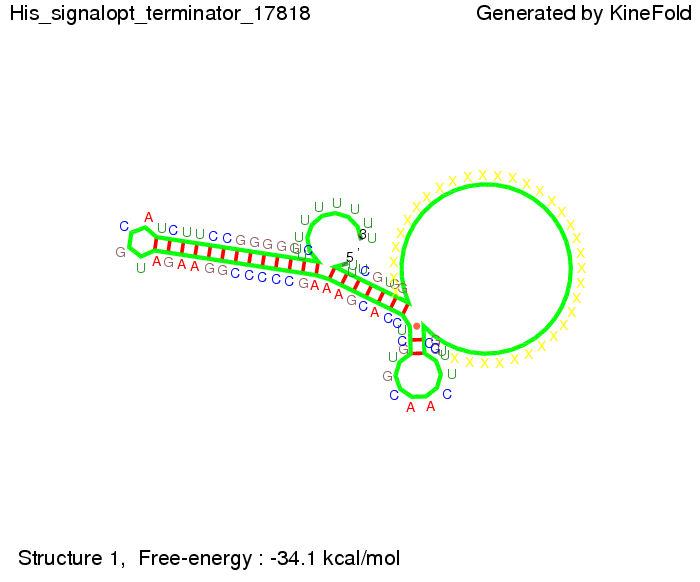
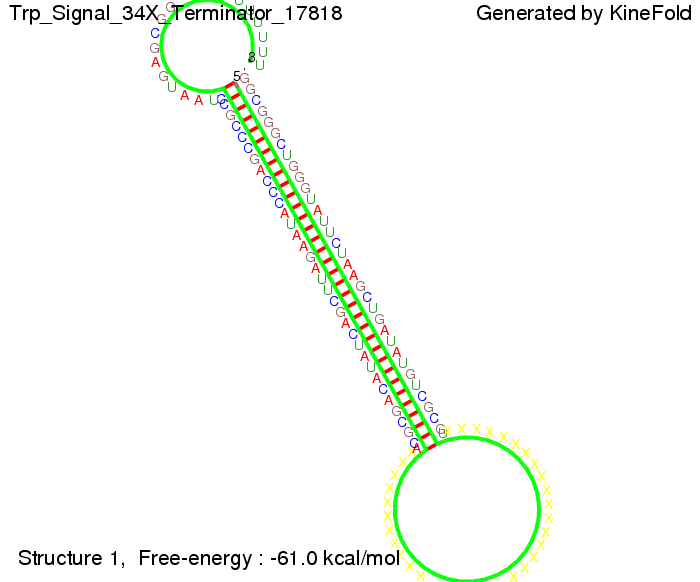
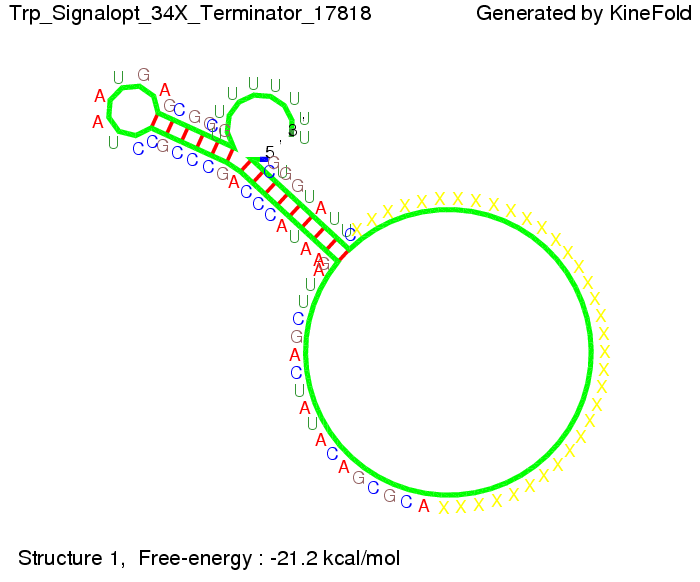
We modeled the signal-terminator interaction for 2, 4-32 nt signal length and proved that the signal sequence binds to the terminator sequence and impedes the terminator folding, thus the polymerase doesn't fall off and the output signal is produced. The minimal free-energy structure of the folded terminator including the random signaling part is shown in the figure "His-terminator" below: Our full signal sequence of length 32 nt completly binds to the terminator and antitermination is successful: On the other hand the picture for a signal length of only 2 nt shows that such a small signal length is not sufficient for antitermination. But already a signal of length 16 nt binds to the terminator so that it cannot fold completely anymore. Furthermore, we explored whether the linker has any influence on the results. As we observed a dependence of the folding time and minimal energy respectively from the linker length we used linkers of length 12, 16, 20, 24, 30, 34, 40, 50, 60, 120 'X' bases. For the minimal energy there is only a very small linker length dependence as one can see in the figure below. The figure also shows that the minimal free-energy structure for the signal sequence bound to the terminator sequence is much more stable, around 35 kcal/mol, than the minimal free-energy structure for the terminator sequence alone. However, for the folding time linker length dependence is significant as one can see in the figure below. But, as, for us, the fact whether the terminator is folding or not is crucial and the videos below show that for appropriate signal length the terminator is not folding. Concerning this fact, for all linker lengths we tested there was only a dependence on the signal length but the results were independent from the linker length. Hence, the linker length dependence can be neglected.
We find that the linker length can be neglected. RNA folding path videosThe video on the left for 16 nt signal length shows that the terminator is already hindered from folding completely and the video on the right, which is done for full signal length of 32 nt, displays that the terminator does not fold at all as the signal immediately binds to the terminator sequence as it is synthesized.
Finally we optimized the signal sequence and obtained a signal sequence of only 8 nt length.
Optimization of the signal sequenceWe also tried to optimize our signal sequence to find the minimal sequence length which still enables antitermination. For this optimization kept the random signaling part constant and varied the part which partially binds to the His-terminator and vice versa to see which length is sufficient for antitermination for each case. Then we combined the results to find a optimal signal.
When varying the part which partially binds to the His-terminator we found that having only the 2 nt of this part together with the random signaling part suffices for antitermination as the picture and the corresponding video below show.
For the full 12 nt of the part which partially binds to the His-terminator, the random signaling part has to have at least 2 nt in order to prevent termination as one can see in the picture below.
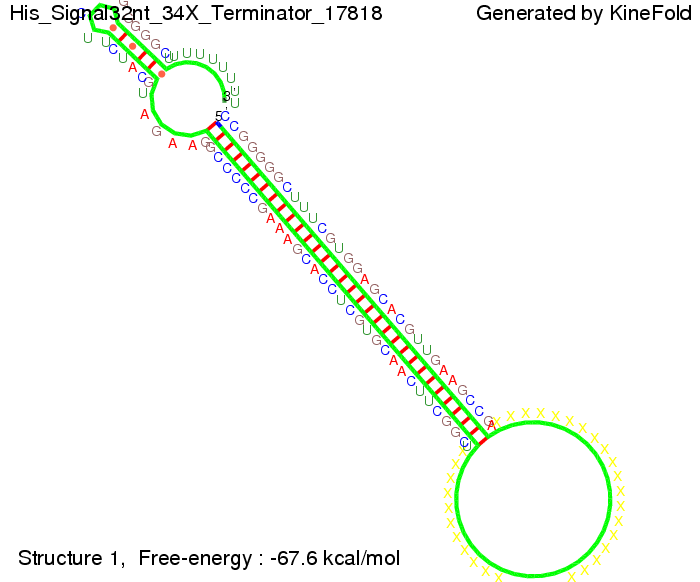
We then combined these two results and found that a signal with overall 8 nt, 4 nt for the random signaling part and 4 nt for the part which partially bind to the His-terminator, 5' UUUCGUGG 3', suffice to enable antitermination as the picture and the corresponding video below display.
Close Close Close ResultsWe showed that in theoretical simulations the His-terminator works perfectly as the terminator itself is relatively stable (minimal free-energy structure is at -31,3 kcal/mol) whereas for appropriate signal length the terminator is not folding at all, that is antitermination occurs before the RNA polymerase can fall off. We also demonstrated that a quite short signal length of 8 nt is sufficient for antitermination to happen (shorter signal length means shorter folding time). II. Trp-terminatorTerminator sequence: Both terminator and signal sequence comprise three parts:
1-2 sentences about the content of the box [TODO]
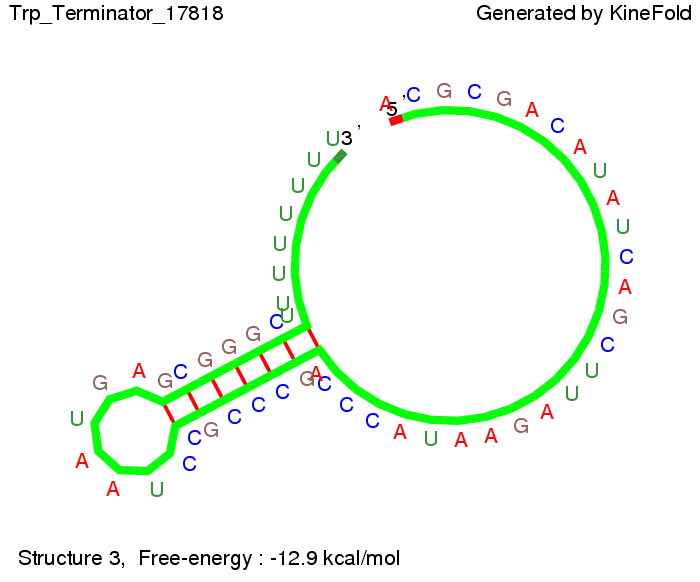
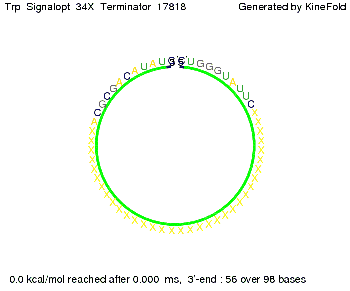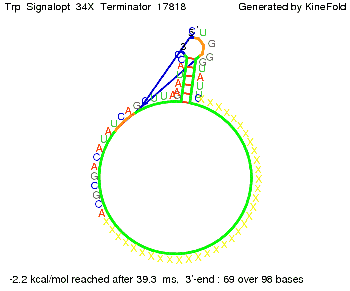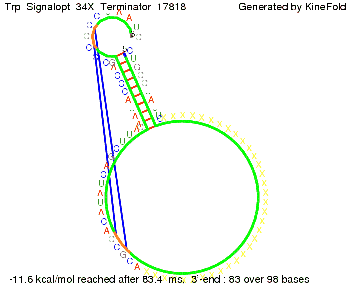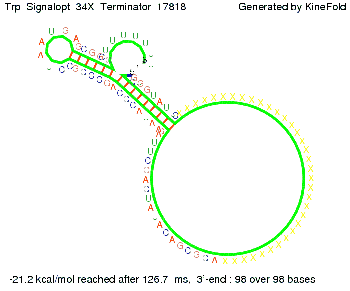
The Trp-terminator turned out to be less stable than the His-terminator. The folded terminator is not the minimal free-energy structure for the given the RNA sequence, it's only the third minimal one at -12.9 kcal/mol compared with the His-terminator which has a minimal free-energy structure at -31.3 kcal/mol. The folded terminator including the natural sequence part upstream of the Trp-terminator binding to the terminator in antitermination state and the random signaling part is shown in the figure "Trp-terminator" below: Our full signal sequence of length 34 nt completly binds to the terminator and antitermination is successful:
Optimization of the signal sequenceAs for the His-terminator, we tried to optimize our signal sequence to find the minimal sequence length which still enables antitermination. It turned out that a signal with overall 10 nt, 2 nt for the random signaling part, all 4 nt for the part which binds to the upstream sequence of the terminator and 2 nt for the part which partially bind to the Trp-terminator, 5' CUGGGUAUUC 3', suffice to enable antitermination as the picture and the corresponding video below display.
ResultsWe showed that in theory the Trp-terminator should function properly. Although the terminator itself is less stable (minimal free-energy structure is at -12,9 kcal/mol) than the His-terminator for appropriate signal length the terminator is not folding, thus antitermination occurs. We also demonstrated that a quite short signal length of 10 nt is sufficient for successful antitermination. III. T7-terminatorTerminator sequence: Both terminator and signal sequence comprise two parts:
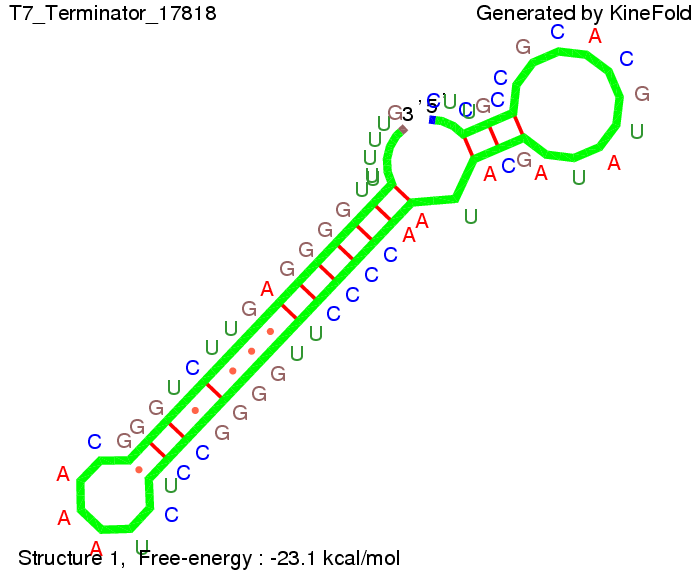
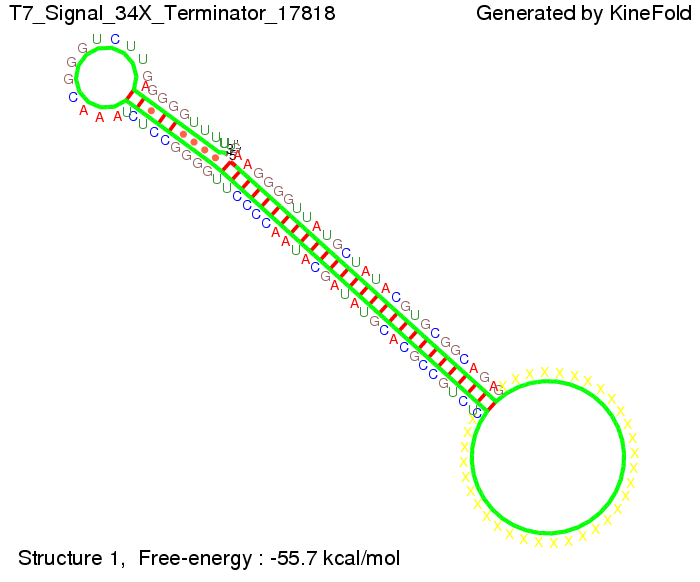
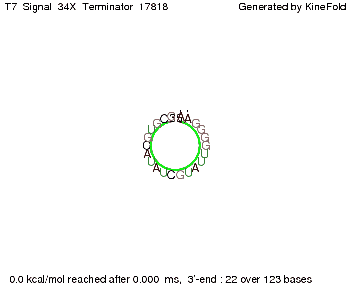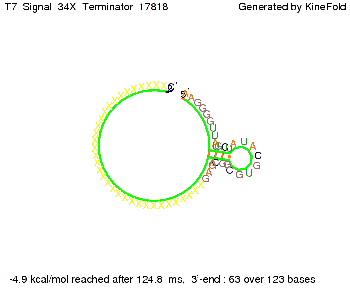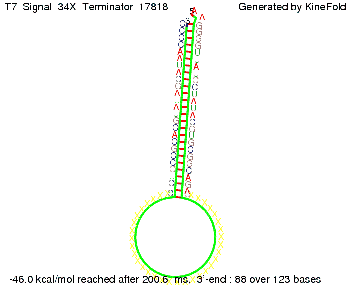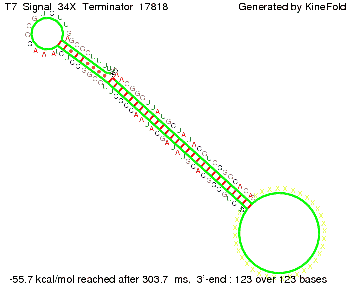
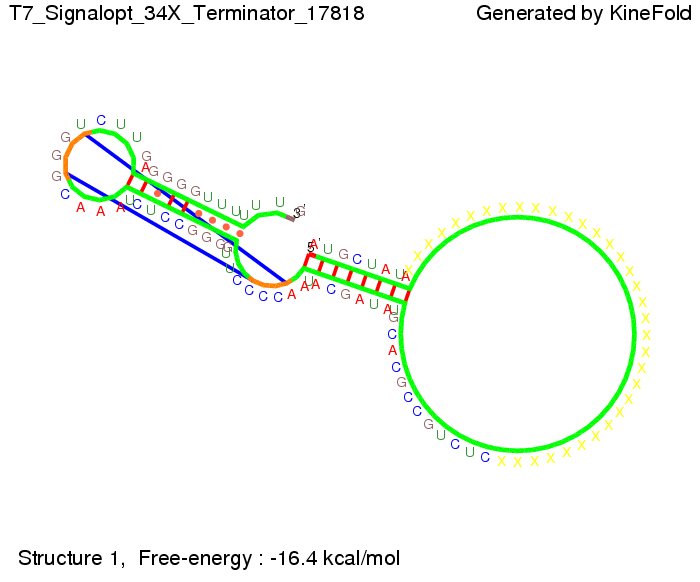
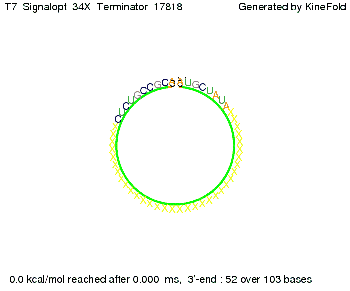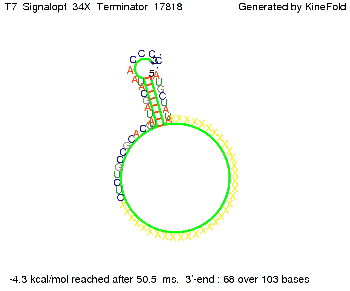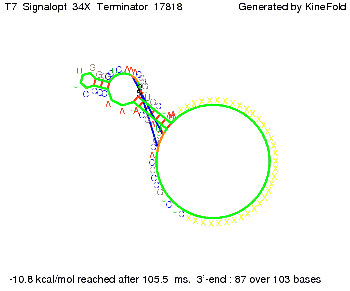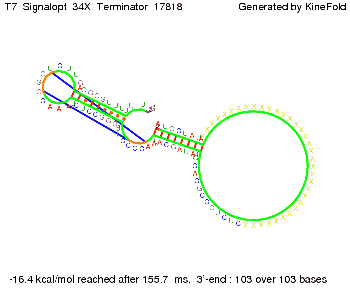
We also modeled the T7-terminator which is also less stable than the His-terminator. Its minimal free-energy structure is at -23.1 kcal/mol. The folded terminator including the random signaling part is shown in the figure "T7-terminator" below: Our full signal sequence of length 28 nt completly binds to the terminator and anti-termination is successful:
Optimization of the signal sequenceAs for the His-terminator, we tried to optimize our signal sequence to find the minimal sequence length which still enables antitermination. We finaly found that a signal with overall 8 nt, 3 nt for the random signaling part and 5 nt for the part which partially bind to the T7-terminator, 5' AUGCUAUA 3', suffice to enable anti-termination as the picture and the corresponding video below display.
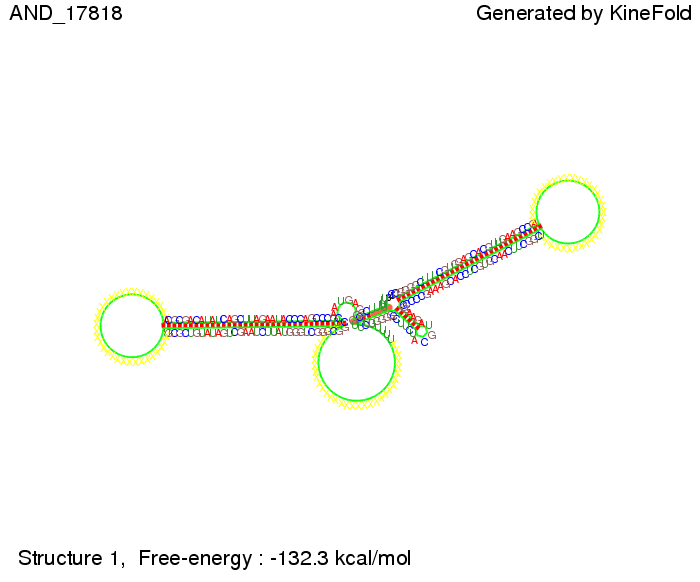
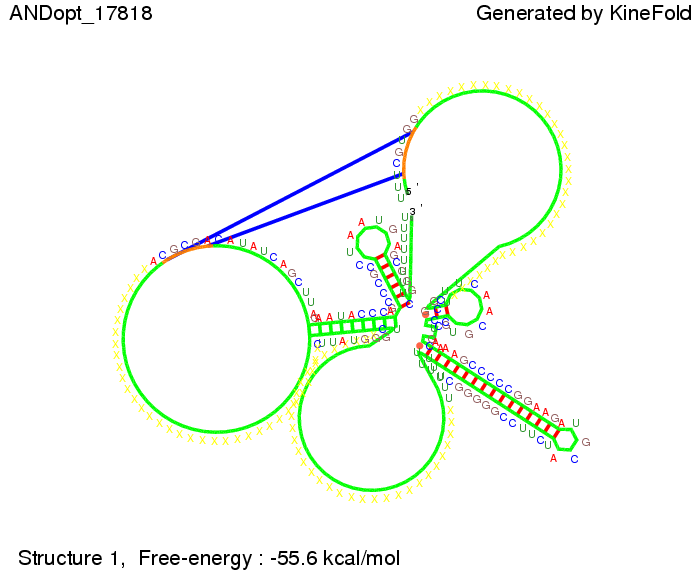
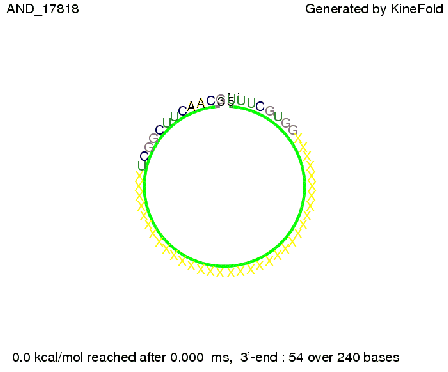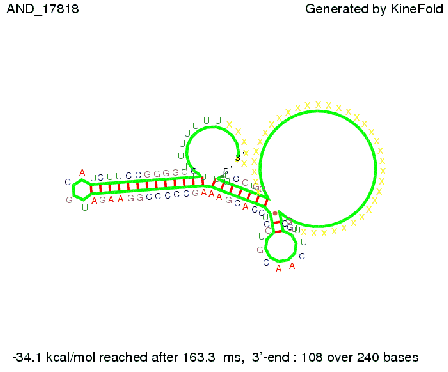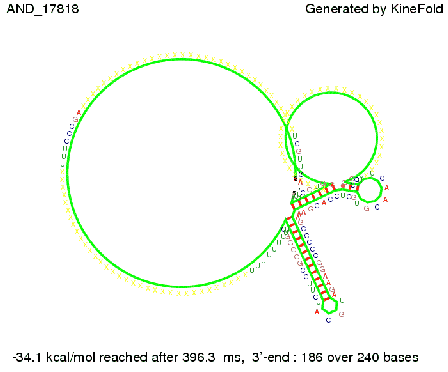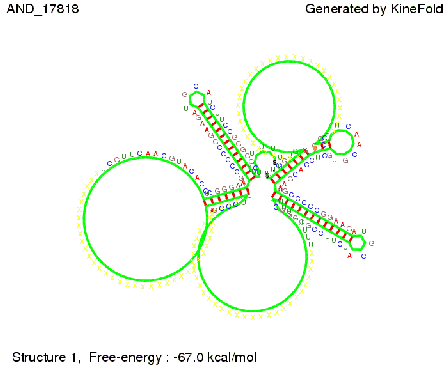
ResultsWe demonstrated that in theoretical simulations the T7-terminator work well. It's less stable (minimal free-energy structure is at -23,1 kcal/mol) than the His-terminator (and rather a lot of bases are unpaired), but its more stable than the Trp-terminator. For appropriate signl length the terminator is not folding at all, that is antitermination occurs. We also demonstrated that a quite short signal length of 8 nt is sufficient for antitermination to happen. Logic gateHere we tried to model a AND gate. We used the His-terminator and two corresponding signals with different random signaling parts. Having different signaling parts is necessary, as if one uses the same one in both signals, the AND gate will always have the output 'true'. This is because the signal sequence would first destroy the first terminator and when the second one is synthesized it might bind to the second one. We linked all the sequences with a 34 X linker. As above both terminator and signal sequences comprise two parts:
His-terminator sequence 1:
As the picture below displays both of the signals successfully bound to the terminators, thus as both input signals are present (that it both input are '1') the AND gate also returns the value '1' as both terminator are destroyed. We also tried to model an AND gate with the optimized signals which also worked as the picture below shows. RNA folding path videosWe created folding path videos for the AND gate. One can see how both signal sequences bind to the terminator sequences as those are synthesized and none of the terminators can fold. For the optimized signal which was sufficient to destroy a single terminator above, the video shows that there are some periods of times when the signal is hindered from binding to the terminator sequence by the other structures, e.g. the linker sequence. CloseResults[TODO] OutlookSo far there is no RNA folding program that is specialized on modeling the interaction of two sequences not to speak of a whole network consisting of RNA based switches and signaling sequences. Combining the concepts of Kinefold[4] and Vienna[5] and using sets of secondary structures that are adjusted to having two sequences instead of only one sequence one could get rid of the bulky linkers. The linkers we used did not play a significant role for our simulation as we were just handling one terminator and one signal sequence, but for larger networks they are likely to be sterically hindering. This obstacle has to be overcome to allow reliable in silcio modeling of RNA devices. With appropriate software RNA devices like our switches could in future be used to interconnect BioBricks, as demonstrated on our Software page, and to simulate those interconnections at elementary step resolution. References[1] A. Xayaphoummine, T. Bucher and H. Isambert, Kinefold web server for RNA/DNA folding path and structure prediction including pseudoknots and knots, 2005, Nucleic Acids Research, Vol. 33, Web Server issue W605–W610. [2] Berg, v. Hippel, 1985. [3] Rippe, Making contacts on a nucleic acid polymer, 2001, TRENDS in Biochemical Sciences. [4] A. Xayaphoummine, T. Bucher, F. Thalmann, and H. Isambert, Prediction and statistics of pseudoknots in RNA structures using exactly clustered stochastic simulations, December 23, 2003, 15310–15315 PNAS vol. 100 no. 26. [5] Christoph Flamm, Walter Fontana, Ivo L. Hofacker, and Peter Schuster, RNA folding at elementary step resolution, RNA (2000), 6:325–338 Cambridge University Press. [6] David H. Mathews, Jeffrey Sabina, Michael Zuker and Douglas H. Turner, Expanded Sequence Dependence of Thermodynamic Parameters Improves Prediction of RNA Secondary Structure, 1999, J. Mol. Biol. (1999) 288, 911-940. |
|||||||||||||||||||
 "
"