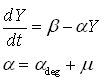Team:TU Delft/Project/rbs-characterization/characterization
From 2010.igem.org

Characterization
By varying only the RBS sequence in a protein generator construct the dependence of the protein expression level on the RBS sequence could be determined by simple fluorescence and biomass curve analysis. The methods are further explained below.
What is RBS strength, really ?
In the field of synthetic biology the 'strength' of an RBS is defined as the rate at which translation is initiated by the RBS sequence on any given mRNA molecule. Going back a step, we see that translation initiation occurs preferentially at certain mRNA sequences, which show a similarity to the consensus -Shine-Delgarno- sequence. This is due to the optimal binding of the 16S rRNA at these regions. In other words, the RBS 'strength' may loosely be defined as the rate of ribosome binding to any given mRNA molecule. (Click here for more information.)
For our project it is not directly the binding equilibria of ribosome to mRNA that is of interest to us, but rather the netto rate of protein production. Thus, in our experimentation we define the RBS strength as the production rate of a given protein downstream of an RBS.
The experiment
The E.coli strains carrying the parts to be tested were cultured for 16 hours on 96-well plates while measuring fluorescence of GFP and biomass absorbance at 10 minute intervals. Click here for the more detailed protocol.
The model
Previous models
We've noticed that previous teams have performed their protein expression rate analysis to only include current protein level (fluorescence measurements) and current biomass concentration (absorption measurements). However, we've found that during measurements, the protein concentration is also influenced by other factors:
- The rapid growth of the bacteria dilutes the protein considerably
- Proteins degrade over time.
See below for more on how we approached these issues.
Growth curve fitting
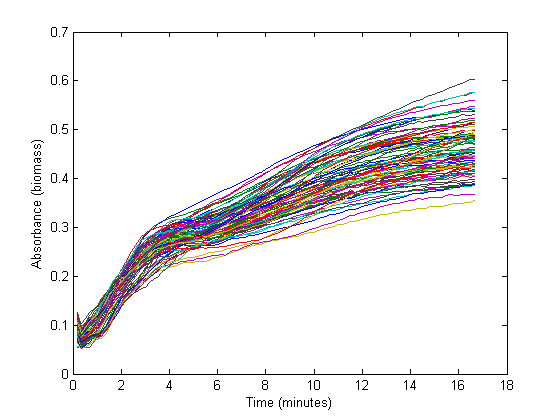
From the biomass, or optical density (OD), graph below, it could be concluded that the fastest growth occurs from 1 hour to 3 hours into the experiment. Within this timespan, it is assumed that growth is exponential, and growth rate can be calculated. The graph below shows 72 growth curves. All in all 12 wells were inoculated per strain carrying a different RBS sequence or 'empty' plasmid (I13401).
The exponential section of this graph was thus curve-fitted to an exponential growth model:
Which resulted in a growth rate ('mu') which was implemented in the dilution factor in the further calculations.
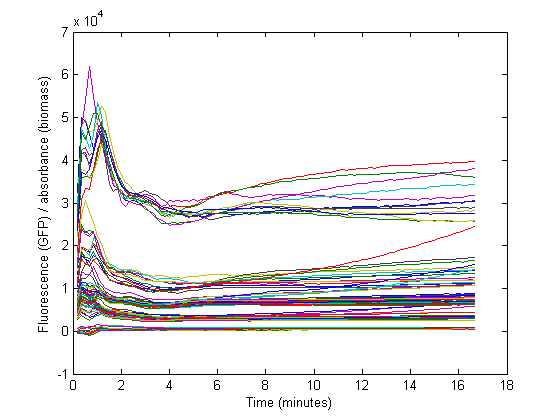
Biomass growth will dilute GFP
The conventional method for characterization of RBS or promotor sequences is to assume that the derivative of the GFP fluorescence is equal to the production rate, as shown in the formula from Kelly et al [1].
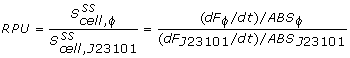
However, this method would only be representable if the strains are subcultured multiple times from the exponential phase. In that case, a steady state GFP concentration (fluorescence) may be assumed and dilution is ignored. Due to the decrease in the biomass specific GFP fluorescence at the start of the measurements it was assumed that dilution effects played an important role in our data and thus was taken into account for our model.
Data normalization method
To go from the raw measurements to the RBS strenghts, we ran the following steps using a matlab script:
the plate reader data consists of 8 rows, each containing multiples of 12:
- 5 strains with Anderson RBSs to be characterized
- B0032 strain to compare to
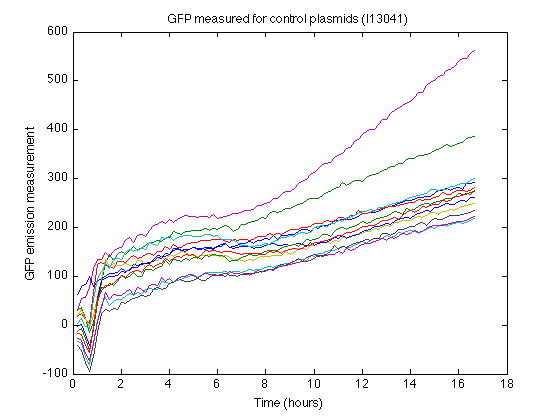
- I13401 strain as control (GFP-dT without promotor and RBS)
- LB+Amp as blank
To prepare the data for further calculation, the following was done:
- Subtract the blank GFP and OD values from the data of wells containing E coli. This takes care of any background noise caused by the LB medium.
- The strain containing I13401 produces some nonzero measurements (See right). From this control strain measurements we can calculate how much 'fake' GFP fluorescence is reported due to biomass or due to leaky expression.
- For each well, we calculate the real GFP that is not a result of biomass or leaky expression:
real_gfp = gfp - fake_gfp_per_od * od
- These values are curve fitted into our protein production model, resulting in a (exponential phase) protein production rate for each well.
Protein production model
As discussed earlier, the protein production model will take dilution into account. Furthermore, the GFP protein used used is stable (half life 41 hours), thus the degradation term is negligible compared to dilution. These assumptions call forth the following formulas:
where:
- Y is the GFP concentration
- Beta is the production rate (the constant that we're interested in)
- Alpha is the sum of the dilution rate and the degradation rate
Converting this equation into an explicit form results in:
The 2 unknown parameters (beta and Y1) could now be curve-fitted against the biomass specific GFP data, using the lsqcurvefit command found in MatLab. The beta constants for each of the 72 wells were then determined and compared to the reference RBS BBa-B0032 to yield the relative RBS strengths listed in the results page.
Source code and data
https://static.igem.org/mediawiki/2010/8/88/TUDelft_2010_RBS_characterization.zip
References
[1] Jason R. Kelly, Adam J. Rubin, Joseph H. Davis, et al (March 2009). "Measuring the activity of BioBrick promoters using an in vivo reference standard". Journal of Biological Engineering 3: 4

 "
"