Team:SDU-Denmark/project-bc

Biochemical Modelling

Motivation

In order to create a flow with bacteria using their flagella movement as the motor it is important to understand bacterial motility and the effects our gen blande noget have on it.
Bacterial motion resembles a random walk, with periods of smooth swimming interrupted by brief tumbles that change the swimming direction. Chemotaxis is achieved by modulation of the tumbling frequency.
In our case we have added phototaxis to E. coli cells making them react to light as well as chemical gradients.
By creating a model describing the key features of the system it will be possible to study the Biochemical behaviour of such a system, and how different parameters will affect it. Before it is implemented in a bacterial strain.

The real system

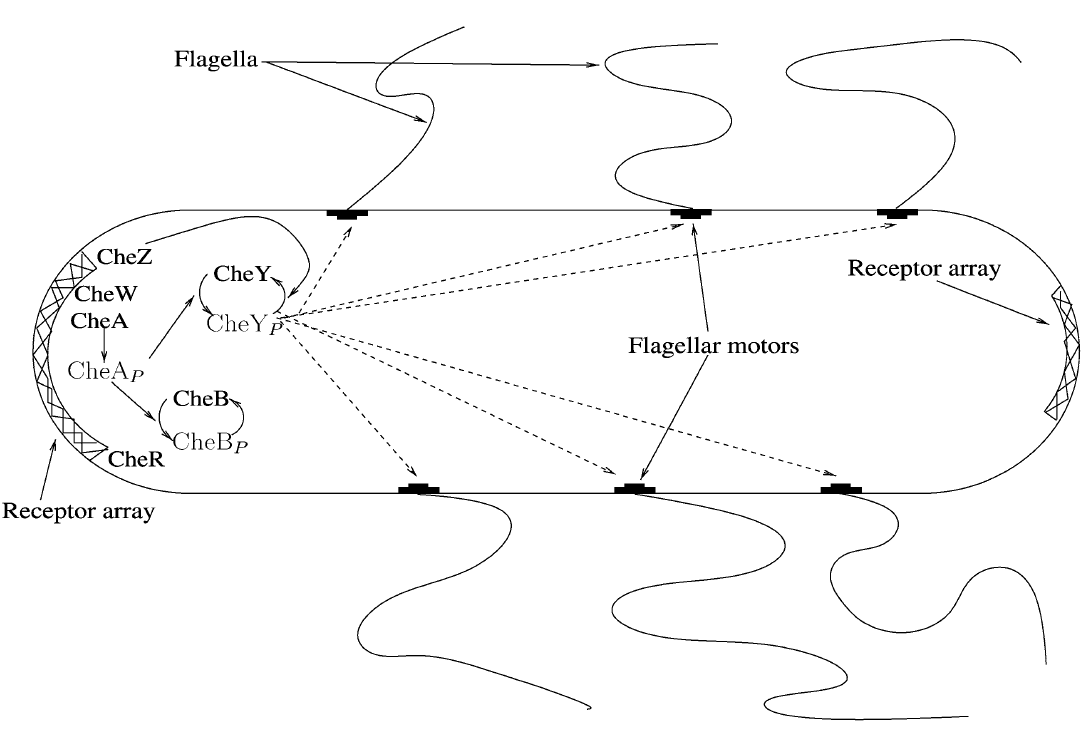
Several chemosensory systems exists in bacteria, the one most studied is the chemotaxis of E. coli. Polar clusters of membrane-spanning methyl accepting chemotaxis proteins (MCPs) are positioned in the ends of the rod shaped E. coli.
Tar (responding to aspartate), Tsr (responding to serine), Tap (responding todipetides), Trg (responding to galactose) ang Aer (responding to oxygen) are the most common receptors seen in E. coli strains.
Transduction of the signal between the MCPs and the flagella motor are managed by a particular fined tuned signalling cascade, which is governed by several intracellular proteins.

Chemotaxis consists of three important phases reaction, adaptation and relaxation. In the reaction phase one of the MCPs sence the specific chemical gradient it responds to, the membrane protein activates the CheW enzym.
The active CheW enzyme suppresses the auto-phophorylation of the CheA enzyme, when no or only a small amount of CheA enzymes are phosphorylated, no phophorylation of the CheY and CheB enzyme accurse, which in the end increases run, because its phosphorylated CheY that binds to the flagella motors and induce tumbling.
When the bacteria have reached the area with a higher concentration of the chemical creating the gradient adaptation sets in.
Because no CheB have been phosphorylated during the reaction period CheR is “allowed” to methylate the MCPs, which increases the auto-phophorylation of the CheA enzyme. The indcreas in auto-phophorylation of CheA results in phophorylation of CheY that leads to tumbling of the bacteria. In the last phase relaxation the CheB have again been phosphorylated by CheA and are now able to demethylate the MCPs, returning the bacteria to its normal run/tumble frequency with a 0,1 second long tumbling period every 1 second.
One other thing to consider in the model is the distance from the to the flagella motors that are randomly located on the entire cell body.
Several modelling methods have been proposed to nearly all of the models include these four items: “Attractant is assumed to be in axcess and binding is assumed to be rapid. One of the most common receptor types to be modelled is the Tar receptor.
This is not unexpected given that a large degree of the experimental literature has focused on the response of E. coli to aspirate which is detected by this receptor. Tar is also one of the most abundant receptors within the cytoplasmic membrane.
In models which have focused on the adaptation and/or the phosphorylation cascade, receptors are commonly modeled as complexes consisting of MCP, CheW and CheA. This is justified by the tight association of CheW and CheA to the MCP recptors.
Descriptions of the motor bias. Given the limited detail available on the interactions of both CheYp and CheY with the cytoplasmic FliM end of flagella motors and that this interaction may be quite complex, it has been a common, simplifying assumption of a number of authors that the fraction of time a motor spends spinning counter-clockwise can be expressed in terms of CheYp by a Hill function. Such reactions are based upon experimental observations.

Description of the model

The model of the system we will be using to predict biochemical behaviour of the system is a simplification of the real system.
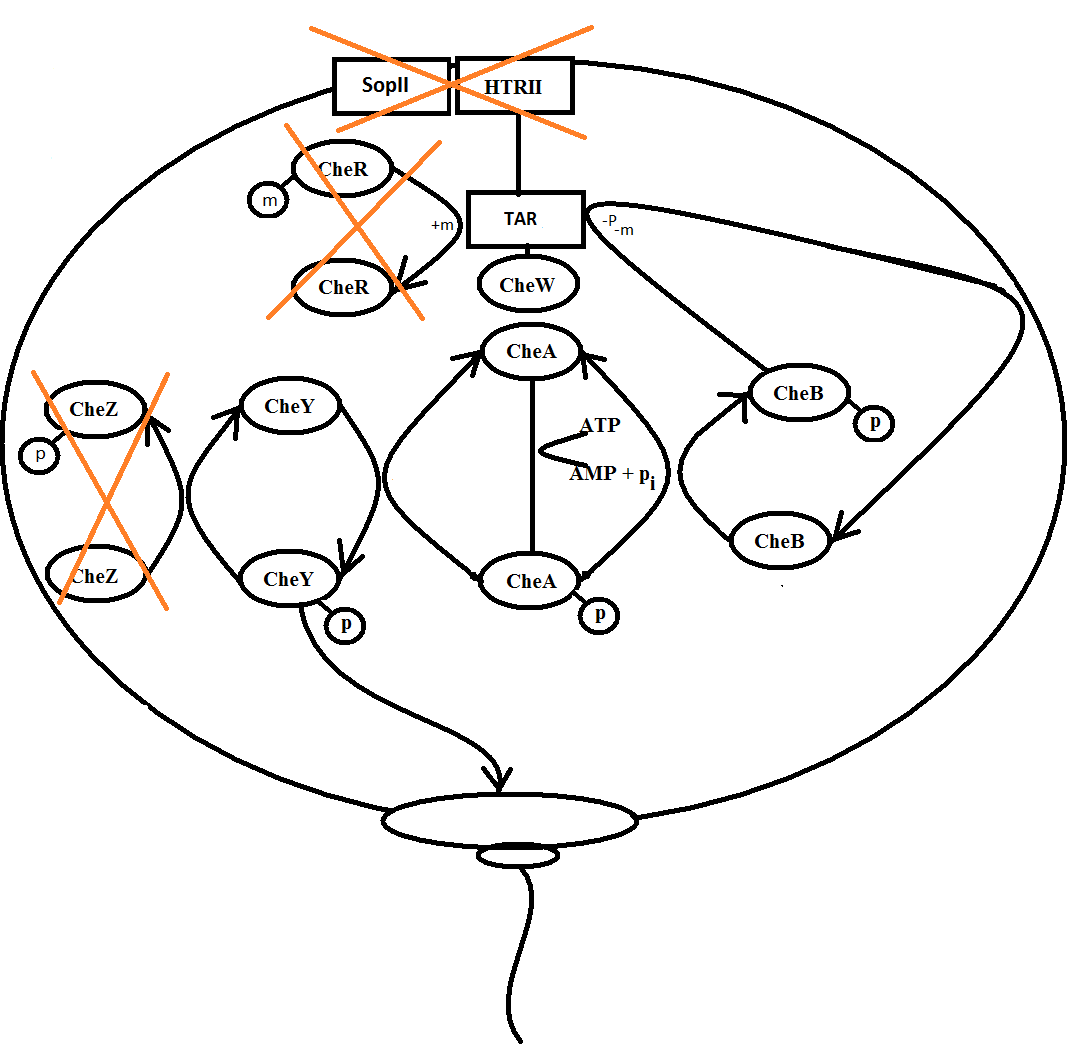
The simplified model doesn’t consider the normal metabolism in the cell it only includes the most important enzymes in the normal E. coli chemotaxis pathway and the proteins responsible for coupling the phototaxis to the chemotaxis.
Beneath you will se a schematics over the system modelling was performed on, the enzymes and proteins with a red cross over them have not been modelled as a differential equation but considered as an constant in the system.

The important enzymes in the system is mathematically represented by a differential equation under the assumption of steady state in the system and modelled in a demo version of the program [http://www.berkeleymadonna.com/ Berkeley Madonna].
When light hits the receptor SRII the signal is transduced thuogth the HTRII and TSR on to the enzyme CheW and activates it, because it’s a straight forward signal transduction the proteins SRII and HTRII is not considered in the model and the equation for the activation of CheW is:
When the CheW enzyme is activated it induces auto-phophorylation of CheA, the phosphorylated CheA can phosphorylate the enzymes CheY and CheB, the equation for CheAp concentration is given by:
Phosphorylated CheY is produced by phophorylation of CheA and removed by CheZ which in this model is defined by a constant, this can be described mathematically by this equation:
Phosphorylated CheB is produced by phophorylation of CheA removed when TSRm is demethylated, this can be described mathematically by this equation:
Methylated TSR is constantly produced by the CheR enzyme which in this model is a constant, the demethylation is preformed by CheBp, the TSRm concentration can bescribed by this equation:
In Berkeley Madonna it’s possible to define different parameters as sliders which enables the user to change parameters continually while the model is running, the sliders used in the model is:

Model results

References

[1] M.J. Tindall, S.L. Porter, P.K. Mainia, G. Gaglia, J.P. Armitage [http://www.springerlink.com/content/f602r72767124602/ Overview of Mathematical Approaches Used to Model Bacterial Chemotaxis I: The Single Cell] Bulletin of Mathematical Biology (2008) 70: 1525–1569

We know what we expect from our system, but does the math agree?