Team:TU Delft/Modeling/HC regulation
From 2010.igem.org
Hydrocarbon regulated expression system
- replace equations with pictures
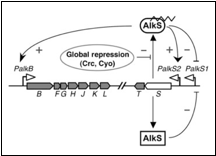
The regulation in P. putida is shown in the following figure;
In figure 1 there is an oversight of the alkane sensing system as it is found in P. putida.
[Picture of the system]
The sensor molecule of this system is AlkS. AlkS can bind to alkanes and form the complex AlkS-HC (HC is short for hydrocarbon). In reality this happens in the membrane and the complex then migrates into the cell and binds to DNA. In the model however everything is assumed to happen in the cytosol.
The AlkS has a self-regulation through two promoters, pAlkS1 and pAlkS2. pAlkS1 is inhibited by binding to any form of AlkS and pAlkS2 is induced by binding to AlkS-HC. The promoters are independent of each other. The alkane degradation pathway the AlkBFGHJKLT operon (AlkB for short) is regulated by the pAlkB promoter and is also induced by AlkS-HC.
This resulting logic is displayed in table 1. System input: Alkane concentration AlkS level AlkB level None Low None High High Very high
AlkS is a sensing molecule and is maintained at low levels in absence of alkanes. This is done by promoter pAlkS1. pAlkS1 is inhibited by any form of AlkS and reaches therefore steady state with a basal level of AlkS. When alkanes are present the target of the cell is to produce AlkB as quickly as possible. To do this AlkS levels are increased because of the binding of alkanes with AlkS, which forms AlkS-HC, which activates pAlkS2. This increases AlkS levels, which inhibits pAlkS1, but pAlkS2 keeps being active because of the presence of both alkanes and AlkS. The presence AlkS-HC simultaneously activates pAlkB. The levels AlkB should be higher than AlkS, as AlkB is an enzyme, while AlkS is a sensing molecule.
-Global regulation -pCaif
Equations
It is assumed that the binding of alkanes to AlkS goes so fast that it can be considered in equilibrium. The binding of AlkS to alkanes is described by an equilibrium equation; K_HC = [AlkS][HC]/[AlkS-HC]
The production of mRNA from the DNA is described by an ODE;
d[mRNA_AlkS]/dt = beta_max_S1 * f_pAlkS1 * c_pAlkS1 + beta_max_S2 * f_pAlkS2 * c_pAlkS2 - (mRNA_degradation + mu) * mRNA_AlkS
d[mRNA_AlkB] /dt = beta_max_B * f_pAlkB * c_pAlkB
- (mRNA_degradation + mu) * mRNA_AlkB
The f stands for a function that describes the activity of a promoter with a Hill functions; f_pAlkS1 = 1 - (AlkS_tot^2/(K_S1^2 + AlkS_tot^2)) f_pAlkS2 = AlkS_HC^2/(K_S2^2 + AlkS_HC^2) f_pAlkB = AlkS_HC^2/(K_B^2 + AlkS_HC^2)
pAlkS1 inhibits when it is bound so it has a reverse effect. The beta-values in the ODE are lumped parameters for promoter strength and transcription speed. c_promoter is the concentration promoter in the cell.
The change in protein concentration is also described by an ODE; d[AlkS]/dt = beta_max_AlkS * mRNA_AlkS - (AlkS_degradation + mu) * AlkS_tot
d[AlkB]/dt = beta_max_AlkB * mRNA_AlkB - (AlkB_degradation + mu) * AlkB
Here the beta-values are a lumped value for rbs strength and transcription speed.
Assumptions
A cell has a volume of 1 μm3, to convert amount of molecules per cell to a concentration the following number was used;
10^-6 μmol mol^-1 / (1 μm^3 * 10^-15 L μm^-3 * 6.02214179 * 10^23 mol^−1) = 1.66 * 10^-3 μM molecule^-1
mRNA has a lifetime of around 5 minutes in the cell to translate this into a degradation constant for the ODE, it is assumed that 90% of the mRNA molecules degrade in 5 minutes. This gives the following degradation constant for mRNA; -1/300 s * log(0.1) = 7.675 * 10^-3 s^-1
For the proteins a lifetime of an hour is estimated; -1/3600 s * log(0.1) = 6.396 * 10^-4 s^-1
When there are no alkanes present only pAlkS1 is active and all other promoters are completely inactive. It is assumed that in this state there are 25 molecules of AlkS and 5 molecules of mRNA for AlkS are present. It is also assumed that the copy number is 1 and a growth rate of 0.1 h^-1 is assumed. pAlkS1 is assumed to be 50% active in this situation, solving the Hill equation gives a K value of; K_S1 = 25 molecules * 1.66 * 10^-3 μM molecule^-1 = 0.166 μM
This reduces the ODEs for AlkS to;
d[mRNA_AlkS]/dt = beta_max_S1 * f_pAlkS1 * c_pAlkS1 - (mRNA_degradation + mu) * mRNA_AlkS
d[AlkS]/dt = beta_max_AlkS * mRNA_AlkS - (AlkS_degradation + mu) * AlkS_tot
Solving this for steady state gives; Beta_max_S1 = 7.703 * 10^-2 Beta_max_AlkS = 3.337 * 10^-3
For full expression of AlkS with high alkane concentration it is assumed that the concentration of AlkS increases 5-fold to 500 molecules. AlkB is assumed to have a concentration of around 1000 molecules. These concentrations are assumed to be reached when the alkane concentration reaches 1 μM. Most of the alkane should be free to be degraded so it is assumed that only 1% of the alkanes is bound to AlkS in this situation. This gives a K value of; K_HC = 41.10
For pAlkS2 and pAlkB 99% activity is assumed; K_S2 = 1.005 * 10^-3 K_B = 1.005 * 10^-3
At this AlkS level pAlkS1 should become virtually inactive and the ODEs reduce to; d[mRNA_AlkS]/dt = beta_max_S2 * f_pAlkS2 * c_pAlkS2 - (mRNA_degradation + mu) * mRNA_AlkS
d[mRNA_AlkB]/dt = beta_max_B * f_pAlkB * c_pAlkB
- (mRNA_degradation + mu) * mRNA_AlkB
d[AlkS]/dt = beta_max_AlkS * mRNA_AlkS - (AlkS_degradation + mu) * AlkS_tot
d[AlkB]/dt = beta_max_AlkB * mRNA_AlkB - (AlkB_degradation + mu) * AlkB
Solving this for steady state gives; beta_max_S2 = 0.1556 beta_max_B = 0.3890 beta_max_AlkB = 3.337 * 10^-3
- link to the experimental part?
Go back
 "
"