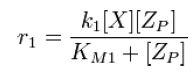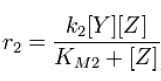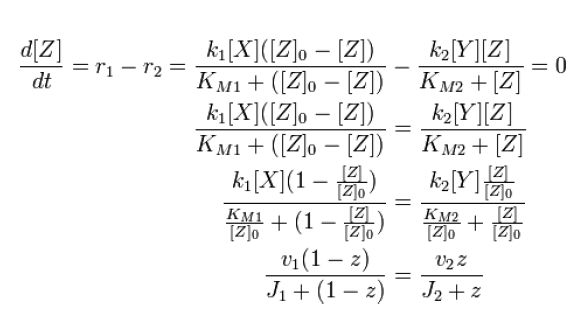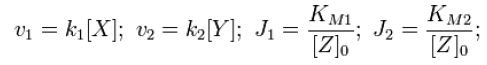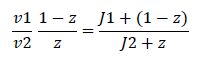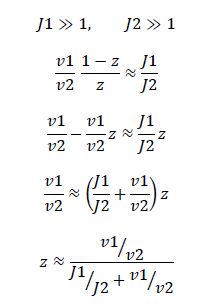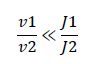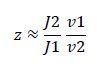Team:Stanford/Research/Modeling

From 2010.igem.org

(Difference between revisions)
(→Kinase/Phosphatase System)
(→sRNA System)
Line 9: Line 9:
-
===sRNA System===
 
-
 
-
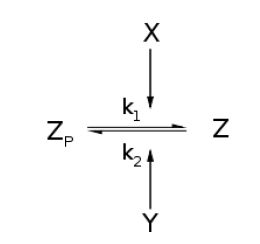
Boolean model for the sRNA system. This is mean to provide a significantly simplified mathematical understanding of the dynamics involved.
 
-
 
-
<html>
 
-
<head>
 
-
      <meta http-equiv="Content-Type" content="text/html; charset=utf-8">
 
-
  <!--
 
-
This HTML is auto-generated from an M-file.
 
-
To make changes, update the M-file and republish this document.
 
-
      --><title>iGEM_boolean_sRNA_model</title><meta name="generator" content="MATLAB 7.10"><meta name="date" content="2010-10-27"><meta name="m-file" content="iGEM_boolean_sRNA_model"><style type="text/css">
 
-
 
-
body {
 
-
  background-color: white;
 
-
  margin:10px;
 
-
}
 
-
 
-
h1 {
 
-
  color: #990000;
 
-
  font-size: x-large;
 
-
}
 
-
 
-
h2 {
 
-
  color: #990000;
 
-
  font-size: medium;
 
-
}
 
-
 
-
/* Make the text shrink to fit narrow windows, but not stretch too far in
 
-
wide windows. */
 
-
p,h1,h2,div.content div {
 
-
  max-width: 600px;
 
-
  /* Hack for IE6 */
 
-
  width: auto !important; width: 600px;
 
-
}
 
-
 
-
pre.codeinput {
 
-
  background: #EEEEEE;
 
-
  padding: 10px;
 
-
}
 
-
@media print {
 
-
  pre.codeinput {word-wrap:break-word; width:100%;}
 
-
}
 
-
 
-
span.keyword {color: #0000FF}
 
-
span.comment {color: #228B22}
 
-
span.string {color: #A020F0}
 
-
span.untermstring {color: #B20000}
 
-
span.syscmd {color: #B28C00}
 
-
 
-
pre.codeoutput {
 
-
  color: #666666;
 
-
  padding: 10px;
 
-
}
 
-
 
-
pre.error {
 
-
  color: red;
 
-
}
 
-
 
-
p.footer {
 
-
  text-align: right;
 
-
  font-size: xx-small;
 
-
  font-weight: lighter;
 
-
  font-style: italic;
 
-
  color: gray;
 
-
}
 
-
 
-
  </style></head><body><div class="content"><pre class="codeinput">clear <span class="string">all</span>
 
-
clc
 
-
 
-
<span class="comment">%Constants and Values</span>
 
-
trackingNum = 6;    <span class="comment">%mRNA_pA, mRNA_pB, sRNA_A, sRNA_B, protein_A, protein_B;</span>
 
-
inputNum = 2;      <span class="comment">%A, B;</span>
 
-
processNum = 6;    <span class="comment">%Trx_pA, Trx_sRNA_A, Trx_pB, Trx_sRNA_B, Trl_A, Trl_B;</span>
 
-
 
-
<span class="comment">%Cell/Matrix Dimensions</span>
 
-
m = 2^trackingNum;
 
-
n = 2^inputNum;
 
-
c = cell(m+1, n+1);
 
-
 
-
trackingMatrix = de2bi(0:m-1);
 
-
inputMatrix = de2bi(0:n-1);
 
-
processMatrix = zeros(1,processNum);
 
-
 
-
<span class="comment">%Populating the Cell (Tracking x Input)</span>
 
-
c{1,1} = [0];
 
-
<span class="keyword">for</span> j = 1
 
-
    <span class="keyword">for</span> i = 2:m+1
 
-
        c{i,j} = trackingMatrix(i-1,:);
 
-
    <span class="keyword">end</span>
 
-
<span class="keyword">end</span>
 
-
<span class="keyword">for</span> i = 1
 
-
    <span class="keyword">for</span> j = 2:n+1
 
-
        c{i,j} = inputMatrix(j-1,:);
 
-
    <span class="keyword">end</span>
 
-
<span class="keyword">end</span>
 
-
<span class="keyword">for</span> i = 2:m+1
 
-
    <span class="keyword">for</span> j = 2:n+1
 
-
        c{i,j} = processMatrix;
 
-
    <span class="keyword">end</span>
 
-
<span class="keyword">end</span>
 
-
 
-
<span class="comment">%Rules, Acessing, and Changing</span>
 
-
<span class="keyword">for</span> j = 2:n+1
 
-
    A = c{1,j}(1);
 
-
    B = c{1,j}(2);
 
-
 
-
    <span class="keyword">for</span> i = 2:m+1
 
-
        mRNA_pA = c{i,1}(1);
 
-
        mRNA_pB = c{i,1}(2);
 
-
        sRNA_A = c{i,1}(3);
 
-
        sRNA_B = c{i,1}(4);
 
-
        protein_A = c{i,1}(5);
 
-
        protein_B = c{i,1}(6);
 
-
 
-
        <span class="comment">%Trx_pA</span>
 
-
        <span class="keyword">if</span> A == 1
 
-
            c{i,j}(1) = 1;
 
-
        <span class="keyword">end</span>
 
-
 
-
        <span class="comment">%Trx_pB</span>
 
-
        <span class="keyword">if</span> B == 1
 
-
            c{i,j}(2) = 1;
 
-
        <span class="keyword">end</span>
 
-
 
-
        <span class="comment">%Trx_sRNA_A</span>
 
-
        <span class="keyword">if</span> A == 1
 
-
            c{i,j}(3) = 1;
 
-
        <span class="keyword">end</span>
 
-
 
-
        <span class="comment">%Trx_sRNA_B</span>
 
-
        <span class="keyword">if</span> B == 1
 
-
            c{i,j}(4) = 1;
 
-
        <span class="keyword">end</span>
 
-
 
-
        <span class="comment">%Trl_A</span>
 
-
        <span class="keyword">if</span> mRNA_pA == 1 &amp;&amp; mRNA_pB == 0
 
-
            c{i,j}(5) = 1;
 
-
        <span class="keyword">end</span>
 
-
 
-
        <span class="comment">%Trl_B</span>
 
-
        <span class="keyword">if</span> mRNA_pB == 1 &amp;&amp; mRNA_pA == 0
 
-
            c{i,j}(6) = 1;
 
-
        <span class="keyword">end</span>
 
-
 
-
    <span class="keyword">end</span>
 
-
<span class="keyword">end</span>
 
-
 
-
<span class="comment">%Display Results (Column by Column)</span>
 
-
[nrows,ncols]= size(c);
 
-
<span class="comment">%Condense Cell and Display</span>
 
-
<span class="keyword">for</span> i = 1:nrows
 
-
    <span class="keyword">for</span> j = 1:ncols
 
-
        string = num2str(c{i,j});
 
-
        l = length(string);
 
-
        r = 1;
 
-
        s = 1;
 
-
        t = 0;
 
-
 
-
        <span class="keyword">while</span> t ~= 1
 
-
            <span class="keyword">if</span> r == l
 
-
            t = 1;
 
-
            <span class="keyword">end</span>
 
-
 
-
            noSpacesString(s) = string(r);
 
-
            r = r+3;
 
-
            s = s+1;
 
-
        <span class="keyword">end</span>
 
-
        c{i,j} = noSpacesString;
 
-
    <span class="keyword">end</span>
 
-
<span class="keyword">end</span>
 
-
c(:,:)
 
-
 
-
<span class="comment">%Find Steady States and Corresponding Inputs</span>
 
-
counter = 1;
 
-
<span class="keyword">for</span> i = 2:m+1
 
-
    <span class="keyword">for</span> j = 2:n+1
 
-
        <span class="keyword">if</span> c{i,j} == c{i,1}
 
-
            completeMatrix{counter,1} = c{i,j};            <span class="comment">%Steady state values</span>
 
-
            completeMatrix{counter,2} = num2str([i-1,j-1]); <span class="comment">%Location (n x m) within results area</span>
 
-
            completeMatrix{counter,3} = c{1,j};            <span class="comment">%Corresponding input values</span>
 
-
            counter = counter+1;
 
-
        <span class="keyword">end</span>
 
-
    <span class="keyword">end</span>
 
-
<span class="keyword">end</span>
 
-
SS_mXn_Input = completeMatrix
 
-
 
-
time = 0:processNum;
 
-
<span class="comment">%plot(time,,time,,time,,time,,time,,time,)</span>
 
-
 
-
<span class="comment">%New Cell for Specific Cases</span>
 
-
<span class="comment">% d(:,1) = c(:,1);</span>
 
-
<span class="comment">% for j = 2:n+1</span>
 
-
<span class="comment">%    C1 = '0000';</span>
 
-
<span class="comment">%    C2 = '0011';</span>
 
-
<span class="comment">%    C3 = '0100';</span>
 
-
<span class="comment">%    C4 = '0111';</span>
 
-
<span class="comment">%    C5 = '1000';</span>
 
-
<span class="comment">%    C6 = '1011';</span>
 
-
<span class="comment">%    C7 = '1100';</span>
 
-
<span class="comment">%</span>
 
-
<span class="comment">%    a = {C1, C2, C3, C4, C5, C6, C7};</span>
 
-
<span class="comment">%    for b = 1:1:length(a)</span>
 
-
<span class="comment">%        if strcmp(c(1,j),a(b)) == 1</span>
 
-
<span class="comment">%            d(:,b+1) = c(:,j);</span>
 
-
<span class="comment">%        end</span>
 
-
<span class="comment">%    end</span>
 
-
<span class="comment">% end</span>
 
-
<span class="comment">% d</span>
 
-
</pre><pre class="codeoutput">
 
-
ans =
 
-
 
-
    '0'        '00'        '01'        '10'        '11'   
 
-
    '000000'    '000000'    '010100'    '101000'    '111100'
 
-
    '000001'    '000000'    '010100'    '101000'    '111100'
 
-
    '000010'    '000000'    '010100'    '101000'    '111100'
 
-
    '000011'    '000000'    '010100'    '101000'    '111100'
 
-
    '000100'    '000000'    '010100'    '101000'    '111100'
 
-
    '000101'    '000000'    '010100'    '101000'    '111100'
 
-
    '000110'    '000000'    '010100'    '101000'    '111100'
 
-
    '000111'    '000000'    '010100'    '101000'    '111100'
 
-
    '001000'    '000000'    '010100'    '101000'    '111100'
 
-
    '001001'    '000000'    '010100'    '101000'    '111100'
 
-
    '001010'    '000000'    '010100'    '101000'    '111100'
 
-
    '001011'    '000000'    '010100'    '101000'    '111100'
 
-
    '001100'    '000000'    '010100'    '101000'    '111100'
 
-
    '001101'    '000000'    '010100'    '101000'    '111100'
 
-
    '001110'    '000000'    '010100'    '101000'    '111100'
 
-
    '001111'    '000000'    '010100'    '101000'    '111100'
 
-
    '010000'    '000001'    '010101'    '101001'    '111101'
 
-
    '010001'    '000001'    '010101'    '101001'    '111101'
 
-
    '010010'    '000001'    '010101'    '101001'    '111101'
 
-
    '010011'    '000001'    '010101'    '101001'    '111101'
 
-
    '010100'    '000001'    '010101'    '101001'    '111101'
 
-
    '010101'    '000001'    '010101'    '101001'    '111101'
 
-
    '010110'    '000001'    '010101'    '101001'    '111101'
 
-
    '010111'    '000001'    '010101'    '101001'    '111101'
 
-
    '011000'    '000001'    '010101'    '101001'    '111101'
 
-
    '011001'    '000001'    '010101'    '101001'    '111101'
 
-
    '011010'    '000001'    '010101'    '101001'    '111101'
 
-
    '011011'    '000001'    '010101'    '101001'    '111101'
 
-
    '011100'    '000001'    '010101'    '101001'    '111101'
 
-
    '011101'    '000001'    '010101'    '101001'    '111101'
 
-
    '011110'    '000001'    '010101'    '101001'    '111101'
 
-
    '011111'    '000001'    '010101'    '101001'    '111101'
 
-
    '100000'    '000010'    '010110'    '101010'    '111110'
 
-
    '100001'    '000010'    '010110'    '101010'    '111110'
 
-
    '100010'    '000010'    '010110'    '101010'    '111110'
 
-
    '100011'    '000010'    '010110'    '101010'    '111110'
 
-
    '100100'    '000010'    '010110'    '101010'    '111110'
 
-
    '100101'    '000010'    '010110'    '101010'    '111110'
 
-
    '100110'    '000010'    '010110'    '101010'    '111110'
 
-
    '100111'    '000010'    '010110'    '101010'    '111110'
 
-
    '101000'    '000010'    '010110'    '101010'    '111110'
 
-
    '101001'    '000010'    '010110'    '101010'    '111110'
 
-
    '101010'    '000010'    '010110'    '101010'    '111110'
 
-
    '101011'    '000010'    '010110'    '101010'    '111110'
 
-
    '101100'    '000010'    '010110'    '101010'    '111110'
 
-
    '101101'    '000010'    '010110'    '101010'    '111110'
 
-
    '101110'    '000010'    '010110'    '101010'    '111110'
 
-
    '101111'    '000010'    '010110'    '101010'    '111110'
 
-
    '110000'    '000000'    '010100'    '101000'    '111100'
 
-
    '110001'    '000000'    '010100'    '101000'    '111100'
 
-
    '110010'    '000000'    '010100'    '101000'    '111100'
 
-
    '110011'    '000000'    '010100'    '101000'    '111100'
 
-
    '110100'    '000000'    '010100'    '101000'    '111100'
 
-
    '110101'    '000000'    '010100'    '101000'    '111100'
 
-
    '110110'    '000000'    '010100'    '101000'    '111100'
 
-
    '110111'    '000000'    '010100'    '101000'    '111100'
 
-
    '111000'    '000000'    '010100'    '101000'    '111100'
 
-
    '111001'    '000000'    '010100'    '101000'    '111100'
 
-
    '111010'    '000000'    '010100'    '101000'    '111100'
 
-
    '111011'    '000000'    '010100'    '101000'    '111100'
 
-
    '111100'    '000000'    '010100'    '101000'    '111100'
 
-
    '111101'    '000000'    '010100'    '101000'    '111100'
 
-
    '111110'    '000000'    '010100'    '101000'    '111100'
 
-
    '111111'    '000000'    '010100'    '101000'    '111100'
 
-
 
-
 
-
SS_mXn_Input =
 
-
 
-
    '000000'    '1  1'      '00'
 
-
    '010101'    '22  2'    '01'
 
-
    '101010'    '43  3'    '10'
 
-
    '111100'    '61  4'    '11'
 
-
 
-
</pre><p class="footer"><br>
 
-
      Published with MATLAB&reg; 7.10<br></p></div><!--
 
-
##### SOURCE BEGIN #####
 
-
clear all
 
-
clc
 
-
 
-
%Constants and Values
 
-
trackingNum = 6;    %mRNA_pA, mRNA_pB, sRNA_A, sRNA_B, protein_A, protein_B;
 
-
inputNum = 2;      %A, B;
 
-
processNum = 6;    %Trx_pA, Trx_sRNA_A, Trx_pB, Trx_sRNA_B, Trl_A, Trl_B;
 
-
 
-
%Cell/Matrix Dimensions
 
-
m = 2^trackingNum;
 
-
n = 2^inputNum;
 
-
c = cell(m+1, n+1);
 
-
 
-
trackingMatrix = de2bi(0:m-1);
 
-
inputMatrix = de2bi(0:n-1);
 
-
processMatrix = zeros(1,processNum);
 
-
 
-
%Populating the Cell (Tracking x Input)
 
-
c{1,1} = [0];
 
-
for j = 1
 
-
    for i = 2:m+1
 
-
        c{i,j} = trackingMatrix(i-1,:);
 
-
    end
 
-
end
 
-
for i = 1
 
-
    for j = 2:n+1
 
-
        c{i,j} = inputMatrix(j-1,:);
 
-
    end
 
-
end
 
-
for i = 2:m+1
 
-
    for j = 2:n+1
 
-
        c{i,j} = processMatrix;
 
-
    end
 
-
end
 
-
 
-
%Rules, Acessing, and Changing
 
-
for j = 2:n+1
 
-
    A = c{1,j}(1);
 
-
    B = c{1,j}(2);
 
-
   
 
-
    for i = 2:m+1
 
-
        mRNA_pA = c{i,1}(1);
 
-
        mRNA_pB = c{i,1}(2);
 
-
        sRNA_A = c{i,1}(3);
 
-
        sRNA_B = c{i,1}(4);
 
-
        protein_A = c{i,1}(5);
 
-
        protein_B = c{i,1}(6);
 
-
       
 
-
        %Trx_pA
 
-
        if A == 1
 
-
            c{i,j}(1) = 1;
 
-
        end
 
-
       
 
-
        %Trx_pB
 
-
        if B == 1
 
-
            c{i,j}(2) = 1;
 
-
        end
 
-
       
 
-
        %Trx_sRNA_A
 
-
        if A == 1
 
-
            c{i,j}(3) = 1;
 
-
        end
 
-
       
 
-
        %Trx_sRNA_B
 
-
        if B == 1
 
-
            c{i,j}(4) = 1;
 
-
        end
 
-
       
 
-
        %Trl_A
 
-
        if mRNA_pA == 1 && mRNA_pB == 0
 
-
            c{i,j}(5) = 1;
 
-
        end
 
-
       
 
-
        %Trl_B
 
-
        if mRNA_pB == 1 && mRNA_pA == 0
 
-
            c{i,j}(6) = 1;
 
-
        end
 
-
       
 
-
    end
 
-
end
 
-
 
-
%Display Results (Column by Column)
 
-
[nrows,ncols]= size(c);
 
-
%Condense Cell and Display
 
-
for i = 1:nrows
 
-
    for j = 1:ncols       
 
-
        string = num2str(c{i,j});
 
-
        l = length(string);
 
-
        r = 1;
 
-
        s = 1;
 
-
        t = 0;
 
-
       
 
-
        while t ~= 1
 
-
            if r == l
 
-
            t = 1;
 
-
            end
 
-
           
 
-
            noSpacesString(s) = string(r);
 
-
            r = r+3;
 
-
            s = s+1;
 
-
        end
 
-
        c{i,j} = noSpacesString;
 
-
    end
 
-
end
 
-
c(:,:)
 
-
 
-
%Find Steady States and Corresponding Inputs
 
-
counter = 1;
 
-
for i = 2:m+1
 
-
    for j = 2:n+1
 
-
        if c{i,j} == c{i,1}
 
-
            completeMatrix{counter,1} = c{i,j};            %Steady state values
 
-
            completeMatrix{counter,2} = num2str([i-1,j-1]); %Location (n x m) within results area
 
-
            completeMatrix{counter,3} = c{1,j};            %Corresponding input values           
 
-
            counter = counter+1;
 
-
        end
 
-
    end
 
-
end
 
-
SS_mXn_Input = completeMatrix
 
-
 
-
time = 0:processNum;
 
-
%plot(time,,time,,time,,time,,time,,time,)
 
-
 
-
%New Cell for Specific Cases
 
-
% d(:,1) = c(:,1);
 
-
% for j = 2:n+1
 
-
%    C1 = '0000';
 
-
%    C2 = '0011';
 
-
%    C3 = '0100';
 
-
%    C4 = '0111';
 
-
%    C5 = '1000';
 
-
%    C6 = '1011';
 
-
%    C7 = '1100';
 
-
%   
 
-
%    a = {C1, C2, C3, C4, C5, C6, C7};
 
-
%    for b = 1:1:length(a)
 
-
%        if strcmp(c(1,j),a(b)) == 1
 
-
%            d(:,b+1) = c(:,j);
 
-
%        end
 
-
%    end
 
-
% end
 
-
% d
 
-
##### SOURCE END #####
 
-
--></body>
 
-
</html>
 

Revision as of 02:57, 28 October 2010

Home Project Applications Modeling Parts Team Notebook Twitter

Contents

Goals

Our intuition for what makes a good ratio sensor could only take us so far. From the very first stages of design, we wanted to back up and test our ideas with mathematical tools. Luckily, we found that solving the equations of mass action kinetics at steady-state was enough to give us clear design criteria. We present the mathematical basis for sensors that are capable of sensing a single ratio digitally, or many ratios in an analog fashion.

The System

Kinase/Phosphatase System

Throughout this derivation, we refer to Goldbeter and Koshland's seminal work on the kinetics of emzyme pairs [1]. For an opposing pair of enzymes X and Y modifying and unmodifying a substrate Z with modification p, MainGBK.JPG

From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is

R1.JPG [2]

and the rate at which Z is phosphorylated is

R2.JPG [2]

We also know that Z can be modified an unmodified, but its total is conserved: [Z]o = [Zp] + [Z]

At steady state, modification and unmodification rates are equal, leading us to

1stblock.JPG [2]

where

2nd block.JPG [2]


Rearranging gives

3rdblock.JPG.

Now, assume that the two opposing enzymes are nowhere near being saturated with substrate:

4thblock.JPG

So, the fraction of modified substrate is a saturating function of the ratio of inputs. The half-max value is the ratio of the strengths of the two enzymes. The linear regime of this function exists where

5thblock.JPG,

and the fraction of unmodified substrate is a linear function of the ratio of inputs.

6thblock.JPG

We now know that the requirements for this analog ratio sensor are

  1. Consistent relationships between inputs and enzyme activities (non-trivial)
  2. A non-saturating amount of substrate

But what happens if we disobey requirement 1? Let's increase the amount of substrate to saturation so that

7thblock.JPG

8thblock.JPG

When the enzymes are saturated, the only steady-state solution is v1 = v2. Any ratio of v1/v2 below this, and all the substrate becomes modified. Any ratio above and all the substrate becomes unmodified. Simply by changing the concentration of substrate, we have converted our analog ratio sensor to a digital ratio sensor.

The requirements for this digital ratio sensor are:

  1. Consistent relationships between inputs and enzyme activities (non-trivial)
  2. An amount of substrate sufficient to saturate both opposing enzymes

References

[1] [http://www.ncbi.nlm.nih.gov/pubmed/6947258 Goldbeter A, Koshland DE Jr.: An amplified sensitivity arising from covalent modification in biological systems. PNAS. 1981 Nov;78(11)6840-4.]

[2] [http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics Goldbeter-Koshland kinetics In Wikipedia. Retrieved July 13, 2010, from http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics]

Retrieved from "http://2010.igem.org/Team:Stanford/Research/Modeling"