"

From 2010.igem.org

Movement model

.

Analogous to the highly complex signal transduction in chemotaxis there is an equally extensive system on side of the flagella, which is even lower understood. As the movement model is only set up in order to close the feedback chain for testing purposes, a phenomenological implementation will be sufficient.
Brief descriptions about the statistics of E. coli movement can be found in the literature section and therefore the model will be a stochastical one.

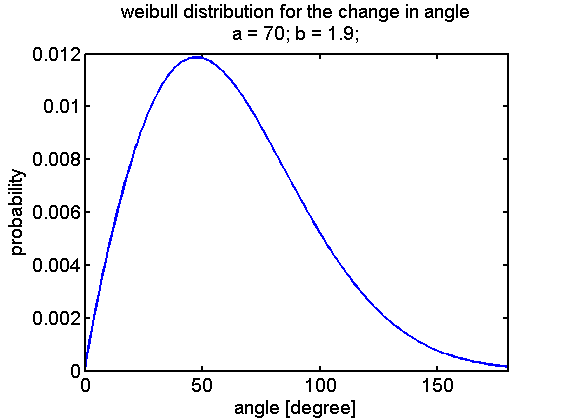
A first implementation was performed by linking the CheYp concentration to the probability of being in the run or tumbling state. These two states either describe the movement and the reorientation as difference equations that can be evaluated at discrete time points. Based on literature statistics about the distribution of change in angle due to tumbling a weibull distribution was selected:

To represent the probability density function it is transformed into a vector that has a frequency of elements that corresponds to the relation of probabilities of the function.

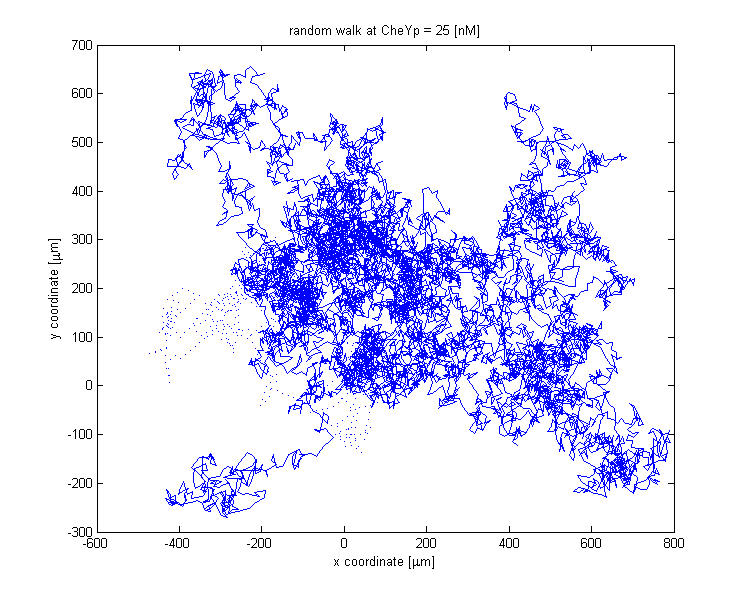
The reorientation happens by selecting a random element of the vector giving the new change in angle. The walks for a thousand steps at different constant CheYp concentrations are shown below:
At a CheYp concentration of 0 the probability for running is about 98%.

At CheYp = 12.5 [nM] both states are equally probable.

At CheYp = 25 [nM] tumbling is dominant.

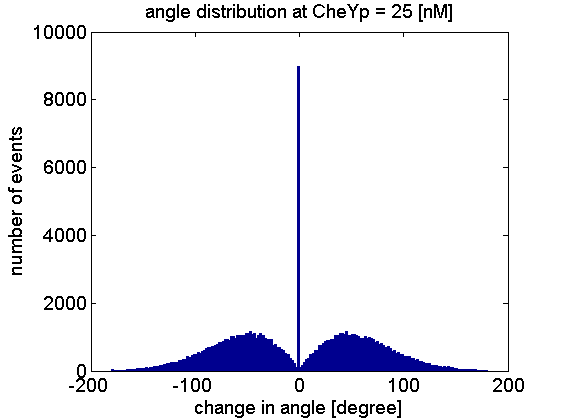
Here is the check of change of angele at 25 [nM] for 1e5 steps: