Team:Stanford/Research/Modeling

From 2010.igem.org

Revision as of 01:26, 28 October 2010 by Drummstikk (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

Goals

Our intuition for what makes a good ratio sensor could only take us so far. From the very first stages of design, we wanted to back up and test our ideas with mathematical tools. Luckily, we found that solving the equations of mass action kinetics at steady-state was enough to give us clear design criteria. We present the mathematical basis for sensors that are capable of sensing a single ratio digitally, or many ratios in an analog fashion.

The System

sRNA System

Boolean model for the sRNA system. This is mean to provide a significantly simplified mathematical understanding of the dynamics involved.

iGEM_boolean_sRNA_model

clear all
clc

%Constants and Values
trackingNum = 6;    %mRNA_pA, mRNA_pB, sRNA_A, sRNA_B, protein_A, protein_B;
inputNum = 2;       %A, B;
processNum = 6;     %Trx_pA, Trx_sRNA_A, Trx_pB, Trx_sRNA_B, Trl_A, Trl_B;

%Cell/Matrix Dimensions
m = 2^trackingNum;
n = 2^inputNum;
c = cell(m+1, n+1);

trackingMatrix = de2bi(0:m-1);
inputMatrix = de2bi(0:n-1);
processMatrix = zeros(1,processNum);

%Populating the Cell (Tracking x Input)
c{1,1} = [0];
for j = 1
    for i = 2:m+1
        c{i,j} = trackingMatrix(i-1,:);
    end
end
for i = 1
    for j = 2:n+1
        c{i,j} = inputMatrix(j-1,:);
    end
end
for i = 2:m+1
    for j = 2:n+1
        c{i,j} = processMatrix;
    end
end

%Rules, Acessing, and Changing
for j = 2:n+1
    A = c{1,j}(1);
    B = c{1,j}(2);

    for i = 2:m+1
        mRNA_pA = c{i,1}(1);
        mRNA_pB = c{i,1}(2);
        sRNA_A = c{i,1}(3);
        sRNA_B = c{i,1}(4);
        protein_A = c{i,1}(5);
        protein_B = c{i,1}(6);

        %Trx_pA
        if A == 1
            c{i,j}(1) = 1;
        end

        %Trx_pB
        if B == 1
            c{i,j}(2) = 1;
        end

        %Trx_sRNA_A
        if A == 1
            c{i,j}(3) = 1;
        end

        %Trx_sRNA_B
        if B == 1
            c{i,j}(4) = 1;
        end

        %Trl_A
        if mRNA_pA == 1 && mRNA_pB == 0
            c{i,j}(5) = 1;
        end

        %Trl_B
        if mRNA_pB == 1 && mRNA_pA == 0
            c{i,j}(6) = 1;
        end

    end
end

%Display Results (Column by Column)
[nrows,ncols]= size(c);
%Condense Cell and Display
for i = 1:nrows
    for j = 1:ncols
        string = num2str(c{i,j});
        l = length(string);
        r = 1;
        s = 1;
        t = 0;

        while t ~= 1
            if r == l
            t = 1;
            end

            noSpacesString(s) = string(r);
            r = r+3;
            s = s+1;
        end
        c{i,j} = noSpacesString;
    end
end
c(:,:)

%Find Steady States and Corresponding Inputs
counter = 1;
for i = 2:m+1
    for j = 2:n+1
        if c{i,j} == c{i,1}
            completeMatrix{counter,1} = c{i,j};             %Steady state values
            completeMatrix{counter,2} = num2str([i-1,j-1]); %Location (n x m) within results area
            completeMatrix{counter,3} = c{1,j};             %Corresponding input values
            counter = counter+1;
        end
    end
end
SS_mXn_Input = completeMatrix

time = 0:processNum;
%plot(time,,time,,time,,time,,time,,time,)

%New Cell for Specific Cases
% d(:,1) = c(:,1);
% for j = 2:n+1
%     C1 = '0000';
%     C2 = '0011';
%     C3 = '0100';
%     C4 = '0111';
%     C5 = '1000';
%     C6 = '1011';
%     C7 = '1100';
%
%     a = {C1, C2, C3, C4, C5, C6, C7};
%     for b = 1:1:length(a)
%         if strcmp(c(1,j),a(b)) == 1
%             d(:,b+1) = c(:,j);
%         end
%     end
% end
% d

ans = 

    '0'         '00'        '01'        '10'        '11'    
    '000000'    '000000'    '010100'    '101000'    '111100'
    '000001'    '000000'    '010100'    '101000'    '111100'
    '000010'    '000000'    '010100'    '101000'    '111100'
    '000011'    '000000'    '010100'    '101000'    '111100'
    '000100'    '000000'    '010100'    '101000'    '111100'
    '000101'    '000000'    '010100'    '101000'    '111100'
    '000110'    '000000'    '010100'    '101000'    '111100'
    '000111'    '000000'    '010100'    '101000'    '111100'
    '001000'    '000000'    '010100'    '101000'    '111100'
    '001001'    '000000'    '010100'    '101000'    '111100'
    '001010'    '000000'    '010100'    '101000'    '111100'
    '001011'    '000000'    '010100'    '101000'    '111100'
    '001100'    '000000'    '010100'    '101000'    '111100'
    '001101'    '000000'    '010100'    '101000'    '111100'
    '001110'    '000000'    '010100'    '101000'    '111100'
    '001111'    '000000'    '010100'    '101000'    '111100'
    '010000'    '000001'    '010101'    '101001'    '111101'
    '010001'    '000001'    '010101'    '101001'    '111101'
    '010010'    '000001'    '010101'    '101001'    '111101'
    '010011'    '000001'    '010101'    '101001'    '111101'
    '010100'    '000001'    '010101'    '101001'    '111101'
    '010101'    '000001'    '010101'    '101001'    '111101'
    '010110'    '000001'    '010101'    '101001'    '111101'
    '010111'    '000001'    '010101'    '101001'    '111101'
    '011000'    '000001'    '010101'    '101001'    '111101'
    '011001'    '000001'    '010101'    '101001'    '111101'
    '011010'    '000001'    '010101'    '101001'    '111101'
    '011011'    '000001'    '010101'    '101001'    '111101'
    '011100'    '000001'    '010101'    '101001'    '111101'
    '011101'    '000001'    '010101'    '101001'    '111101'
    '011110'    '000001'    '010101'    '101001'    '111101'
    '011111'    '000001'    '010101'    '101001'    '111101'
    '100000'    '000010'    '010110'    '101010'    '111110'
    '100001'    '000010'    '010110'    '101010'    '111110'
    '100010'    '000010'    '010110'    '101010'    '111110'
    '100011'    '000010'    '010110'    '101010'    '111110'
    '100100'    '000010'    '010110'    '101010'    '111110'
    '100101'    '000010'    '010110'    '101010'    '111110'
    '100110'    '000010'    '010110'    '101010'    '111110'
    '100111'    '000010'    '010110'    '101010'    '111110'
    '101000'    '000010'    '010110'    '101010'    '111110'
    '101001'    '000010'    '010110'    '101010'    '111110'
    '101010'    '000010'    '010110'    '101010'    '111110'
    '101011'    '000010'    '010110'    '101010'    '111110'
    '101100'    '000010'    '010110'    '101010'    '111110'
    '101101'    '000010'    '010110'    '101010'    '111110'
    '101110'    '000010'    '010110'    '101010'    '111110'
    '101111'    '000010'    '010110'    '101010'    '111110'
    '110000'    '000000'    '010100'    '101000'    '111100'
    '110001'    '000000'    '010100'    '101000'    '111100'
    '110010'    '000000'    '010100'    '101000'    '111100'
    '110011'    '000000'    '010100'    '101000'    '111100'
    '110100'    '000000'    '010100'    '101000'    '111100'
    '110101'    '000000'    '010100'    '101000'    '111100'
    '110110'    '000000'    '010100'    '101000'    '111100'
    '110111'    '000000'    '010100'    '101000'    '111100'
    '111000'    '000000'    '010100'    '101000'    '111100'
    '111001'    '000000'    '010100'    '101000'    '111100'
    '111010'    '000000'    '010100'    '101000'    '111100'
    '111011'    '000000'    '010100'    '101000'    '111100'
    '111100'    '000000'    '010100'    '101000'    '111100'
    '111101'    '000000'    '010100'    '101000'    '111100'
    '111110'    '000000'    '010100'    '101000'    '111100'
    '111111'    '000000'    '010100'    '101000'    '111100'


SS_mXn_Input = 

    '000000'    '1  1'      '00'
    '010101'    '22   2'    '01'
    '101010'    '43   3'    '10'
    '111100'    '61   4'    '11'

Kinase/Phosphatase System

Throughout this derivation, we borrow For an opposing pair of enzymes modifying and unmodifying a substrate,

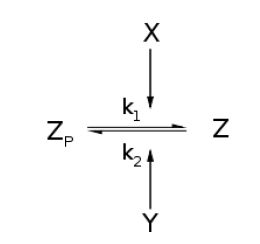
From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is and the rate at which Z is phosphorylated is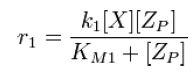

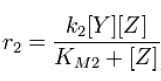
Along with the conservation equation [Z]o = [Zp] + [Z], File:1stblock.jpg Where File:2ndblock.jpg File:3rdblock.jpg Now, assume that the two opposing enzymes are nowhere near being saturated with substrate: File:4thblock.jpg So, the fraction of modified substrate is a saturating function of the ratio of inputs. The half-max value is the ratio of the strengths of the two enzymes. The linear regime of this function exists where File:5thblock.jpg And the fraction of unmodified substrate is a linear function of the ratio of inputs: File:6thblock.jpg So, the requirements for this analog ratio sensor are 1. Consistent relationships between inputs and enzyme activities (non-trivial) 2. A non-saturating amount of substrate 3. A ratio of enzyme activities greater than any ratios we want to measure Now increase the amount of substrate to saturation and File:7thblock.jpg File:8thblock.jpg modified. Any ratio above and all the substrate becomes unmodified. The requirements for this digital ratio sensor are: 1. Consistent relationships between inputs and enzyme activities (non-trivial) 2. An amount of substrate sufficient to saturate both opposing enzymes

References

[1] [http://www.ncbi.nlm.nih.gov/pubmed/6947258 Goldbeter A, Koshland DE Jr.: An amplified sensitivity arising from covalent modification in biological systems. PNAS. 1981 Nov;78(11)6840-4.]]