From 2010.igem.org

Modeling & Simulating Bacterial Movement

Schematical overview of the relation between the chemotaxis pathway and the movement model.

Overview

Analogous to the highly complex signal transduction network in the chemotaxis receptor model, there is an equally challenging molecular mechanism on side of the flagella, responsible for the movement of the bacterium.

In order to capture the features of cell motility, we created a probabilistic two state model, which simulates the cell movement in accordance to the existing empirical observations.

At every time step of the simulation of the cell motility model, the current CheYp concentration is received as an input from the chemotaxis pathway model. This input determines the probability of the CCW and the CW rotation direction of the flagella. A counterclockwise rotation corresponds to the directed movement (running) state and to a change in spatial coordinates, together with a slight change in angle, while a clockwise rotation corresponds to the tumbling state and to a new movement direction, with nearly unchanged other spatial coordinates.

By coupling the probabilistic movement model with the deterministic molecular model we can realistically simulate the variations in motility which occur due to variations in the concentrations of the molecular species of the chemotaxis pathway, namely in the concentration of CheYp.

Known Features of Cell Motility

Bacterial motility has been analyzed since several decades such that many of its properties are well characterized, although the exact molecular mechanisms leading to these properties are still a subject of scientific dispute. Since answering the open questions is beyond the scope of our iGem project, we focused on building a phenomenological model which reliably reproduces the known chemotactic behavior of E. coli cells. For this task we relied on the data provided in [1], which is similar to other data which can be found in the literature, although the exact quantitative data might vary slightly depending on the strains used and the experimental conditions. Thus, our model was required to reproduce the following properties:

• E. coli cells are most of the time in one of two states: They either swim straightly or tumble.
• The time between transitions between the two states is approximately exponentially distributed, with a tumbling time of 0.14±0.19s and a straight swimming time of 0.86±1.18s (each value given as mean and standard deviation) for a constant extracellular environment.
• In a changing extracellular environment (e.g. increasing concentration of Aspartate), mainly the distribution of the straight swimming time adjusts, whereas the distribution of the tumbling time only slightly changes.
• The average speed of an E. coli during straight swimming is approximately 14.2±3.4μm/s, whereas during tumbling the average speed is significantly smaller.
• In a constant environment, the integrated change of the swimming direction during one tumbling is approximately 68±36°, whereas it is only approximately 23±23° during one period of swimming.
• The distribution of the absolute value of the change in direction during one tumbling given in [1] looks similar to a Weibull distribution with a nonzero maximum, whereas the change in direction during straight swimming is maximal at 0&degree;.

Assumptions

Accordance with the experimental data given in [1], the mean tumbling length was assumed to be independent of the intracellular conditions, unlike the mean run length, which is known to differ for wild type cells depending on the extracellular conditions. Besides the experimental evidence in [1], this assumption also has a biological interpretation: tumbling is believed to occur because the flagella push each other away and disassemble after rotating counter-clock wise (directed movement). The duration spent in tumbling is a stochastic variable mainly representing the time the flagella afterward need to reassemble, and a single process of reassembling is only weakly correlated with the frequency of tumbling.

Furthermore, since the speed of an E. coli cell only varies slightly around its mean value during a straight swimming phase (see above), we assumed in our model that the velocity during directed movements is constant and zero during tumbling.

For the change in direction during straight swimming we assumed that the change in angular speed during one straight swimming integration step is Gaussian distributed with zero mean and a standard distribution such that when integrated over an average swimming period length, we obtain the properties described above.

The main challenge for our model was to reproduce the angular change during a tumbling period. Choosing the angular speed independently at every integration step, as for the angular speed during straight swimming, would lead to a distribution of integrated changes in directions with a maximum at zero. However, the observed changes in direction have a distribution with a maximum at around 50&degree;. To overcome this discrepance, we decided to assume a constant angular speed during a whole tumbling period, which was drawn from a distribution which we optimized to as good as possible reflect the observed data.

General Algorithm

Schematic overview of the algorithm used to model chemotaxis motion as influenced by the CheYp level in the cell.

We use a two state model to simulate bacterial motility, with the two states corresponding to directed movement and to tumbling. At each timestep of the simulation, the cell either keeps or switches its state, according to the input received from the molecular model, which determine the transition probabilities between states.

If the model is currently in the straight swimming state, the cell mainly moves in its current direction with a speed of 14.2μm/s and changes this direction only slightly (see [1]).

If however the model is currently in the tumbling state, the cell is changing its direction rapidly while nearly staying at the same point.

Coupling to the Molecular Model of the Chemotaxis Pathway

Bias The sigmoid dependency between CheYp concentration and probability of the cell being in the directed movement state

The quantity that links the CheYp concentration with the type of motion (tumbling vs. directed motion) is called the bias and it is formally defined as the fraction of time spent in the directed movement state with respect to the total time in motion. Our choice for bias formulation was a nonlinear Hill - type function of CheYp concentration, with one of the parameters being the wild-type CheYp concentration for which a steady - state invariant time ratio was obtained. Both the functional dependency and CheYp value are well documented in literature [2].

Since the mean tumbling length is assumed to be independent of the intracellular state, the mean straight swimming length has to be a function of the bias:

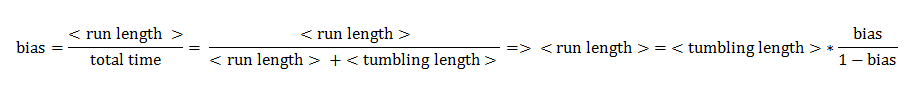
Transition Probabilities (Switching between running and tumbling)

At every time step of the simulation, the model decides probabilistically whether to switch its current state (e.g. to start tumbling) or to keep its state (e.g. continue straight swimming). We implemented this by applying a two - state first - order Markov process, in which the future state is only dependent on the current state. Since we have Boolean values for any possible state, we can define the following four transition probabilities, separately controlled depending on whether the cell is currently in the directive movement or in the tumbling state.



Therefore, the two central parameters of our model are the probabilities of keeping the current state also as future state: the probability that the future state is directed movement, when the current state is directed movement (p1) and probability of the future state being tumbling, when the current state is tumbling (p2).
In deriving the expression of these probabilities, we separately and symmetrically focused on the two processes: directed movement and tumbling. As a consequence, the mean run length is only dependent on the timestep and on the probability of continuing the directed movement (p1), while the mean tumbling length is only dependent on the timestep and on the probability of continuing tumbling (p2).
We will explain in detail the technique employed in deriving the probability of being in the directed movement state, when the previous state was directed movement. The symmetrical calculations, for the mean tumbling length, follow identically.

The mean run length is the expected value of a random variable representing the number of timesteps the cell consecutively spends in directed movement. By expanding the definition of an expected value, the mean run length becomes an infinite sum over all possible consecutive run-lengths, multiplied by their respective occurrence probabilities.

Direction changes

Both, during directed movement periods and during tumbling, the direction the E. lemming swims changes. Although the angular speed is much higher during tumbling periods, it was important also to include the change in angle during directed movement periods, since with our light-induced localization system, we can extend this period significantly, such that even smaller changes in angle during straight swimming become important when integrated over time.

Angular Velocity during Tumbling

As stated above, the observed probability distribution of the absolute value of the integrated change in direction over one tumbling period is not maximal around zero. Instead, it is small for small and high angles with the most probable angles being between 20° and 90°. An intuitive approach, which would set the angular speed to an positive or negative value thrown independently from a some symmetric probability distribution, can not resample such a distribution, since it would always result in a distribution with a maximum being at zero. We thus decided to draw an angular speed constant from an appropriate distribution for the whole tumbling period at the transition time from directed movement to tumbling. However, even with this approach it was not possible to fully resample the quantitative properties of the observed distribution. Searching for the reason for this discrepancy, we had to deduce that the shape of the distribution of the tumbling lengths make it impossible to create a distribution of the integrated angular changes which corresponds in all of its properties to the observed once, without making the angular speed inversely proportional to the tumbling length. Although such an approach is easy to implement, the resulting model would be characterized by a lack of mathematical aesthetic. We thus decided to draw the angular speed from a distribution independent of the tumbling length such that most of the properties of the observed angular distribution are reproduced. This approach results in a distribution having, as the observed one, a nonzero maximum, and a mean between 60° and 70°. However, the standard deviation of our distribution is 47.0°, over 11° higher than the observed one of 36°.

Angular Velocity during Directed Movement

Different to the angular velocity during tumbling, the angular velocity during directed movement can be drawn from an appropriate distribution to resample the experimental measured distributions. The experimentally available data is the mean (23°) and the standard deviation (also 23°) of the absolute value of the change in direction during one straight swimming period. We assumed that the angular speed during one timestep is normally distributed with zero mean and a standard deviation of σ. Thus, when one directed movement period consists of N=<run length>/Δt integration steps, the change in angle after one directed movement period has zero mean and a standard deviation of
σ_run=σ Δt N^½ = σ<run length>^½Δt^½.
The in the literature given values of change in angle are however given as absolute values. This corresponds of calculating the corresponding χ-distribution of the angular change, which has in case the mean value of μ_χ=(2/π)^½σ_run and a standard deviation of σ_χ=σ_run. Since (2/π)^½≈0.8 and thus the resulting mean and standard deviations are similar to each other as experimentally observed, we have chosen a standard deviation of
σ=(π/2)23°<run length>^-½Δt^-½
for our model. The resulting distribution of the angular change during directed movement resamples closely the experimentally available values (see below).

Simulation Results

For our simulations, we have chosen a timestep Δt=0.03s, which is around five times smaller than the smallest time constants in the cell motility model, as well as over ten times smaller than the time constant with which the CheYp concentration changes in the molecular model (for details, see optimal experimental design).

Evaluation of the Model

To evaluate the movement model, we performed several long time simulations under constant conditions (bias set to its wild-type steady state value of around 0.85) and determined its characteristics which might be compared to the known properties of the motility of E. coli cells as given in [1] and described above.

Distribution of the durations of directed movement states. The distribution is approximately exponential with a mean value of 0.87s and a standard deviation of 0.86s.

Distribution of the duration of tumbling states. The distribution is approximately exponential with a mean value of 0.14s and a standard deviation of 0.12s.

Distribution of the absolute value of the angular change integrated over the duration of one directed movement period. The distribution is approximately χ-distributed with mean 20.5° and standard deviation 20.1°.

Distribution of the absolute value of the angular change integrated over the duration of one directed movement period. The distribution has similar properties as the one experimentally observed in [1]. Its mean value is 62.3° and its standard deviation 47.0°.

Variations in input bias

Furthermore, we simulated the spatial behavior of a single E. coli cell under the influence of different input bias values. For a more realistic simulation of the bacterial movement process, the input bias was obtained directly from the combined molecular model linking the chemotaxis pathway and the light switch. As the combined model offered us many design alternatives for performing simulations, we decided on a fixed molecular template, to ease the comparison of results.

The chosen molecular template for simulating the movement model was the following:

• molecular model chosen: Spiro et al. [3]
• controlled Che species: CheY
• Light coupling: CheY-PIF3 & PhyB-Anchor

Each row of the subplots table presented below represents a different input bias value for the movement model, obtained as a result of different input protein concentrations for the combined molecular model. Each column represent a different simulation length (100 seconds, 500 seconds and 3000 seconds).

The input protein concentrations used, together with the corresponding obtained steady-state bias were the following:

All the simulations were run without the existence of any controller algorithm, therefore reproducing the random chemotaxis walk.

Please note the different spatial ranges when comparing the plots, increasing both with increasing simulation time length (the bacterium travels a longer distance in a longer time period) and with increasing bias value (the probability of choosing the directed movement state increases, therefore, on average, the cell travels a longer distance).

Bacterial random walk for different input bias values and different simulation times The plots were generated under different initial conditions of the molecular model, resulting in different values for the input bias. As seen if analyzing the plots row-wise, an increasing bias value leads to increasing directed movement periods. The culminating point is a bias value of 0.99, equivalent to almost continuous directed movements. To be also noted is the gradual smoothing of direction changes between directed movement states, with increasing bias value. The effect of the simulation time can be seen if analyzing the plots column-wise. The same movement pattern observed during the first 100 seconds is repeated over a longer time period, providing an overview of the long - term chemotaxis spatial behavior.
Note the increasing axis range, both on the x and on the y coordinate, due to both increasing bias value and increasing simulation time.

Directed movement/Tumbling

For the above simulated trajectories, we generated the so-called directed movement/tumbling plots used in analyzing chemotaxis motility from the perspective of boolean movement - time dependency. For providing a better visibility of the individual steps of the movement process, in the left figure only the first 60 seconds of the above simulations were considered, while in the right figure a detailed insight into the first 30 seconds is provided.

The directed movement tumbling plots for two different input bias values for 60 seconds simulation time Movement value of 1 represents the directed movement state, while movement value of 0 represents the tumbling state. Simulation time was 60 seconds, with sampling at every 0.03 seconds. As expected, the density of the plots is decreasing with increasing bias value, since the ratio directed movements/tumbling is increasing. In the limit case of 0.99 bias, the tumbling periods are not noticeable, the bacterial behavior consisting almost entirely of tumbling.

The directed movement tumbling plots for two different input bias values for 30 seconds simulation time The effect of the input bias is even more visible at a higher resolution. For lower bias value, tumbling occurs more often (upper plot) and it is gradually eliminated with increasing bias.

Download

The bacterial movement model is included within the Matlab Toolbox and can be downloaded there.

References

[1] [http://www.nature.com/nature/journal/v239/n5374/abs/239500a0.html H.C. Berg, D.A.Brown: Chemotaxis in Escherichia coli analysed by three - dimensional Tracking. Nature 1972 239, 500 - 504]

[2] [http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1299372/?tool=pubmed Levin, Morton-Firth: Origins of Individual Swimming Behavior in Bacteria, Biophysical Journal 1998 74:175-181]

[3] [http://www.pnas.org/content/94/14/7263.full Spiro et al: A model of excitation and adaptation in bacterial chemotaxis. PNAS 1997 94;14;7263-7268.]