Team:ETHZ Basel/Modeling/Sorokina

From 2010.igem.org

Background

To model the light-induced relocation system, our first approach was to implement and adjust the recently published model by Sorokina et al [1]. Although we succeeded to re-implement this model as published in the paper, we decided to not use it for our project. This section gives a short review on the model, and, at the end of this page, we shortly summarize the reasons for our decision.

General remarks

In [1] Sorokina et al developed (in vivo) and modeled (in silico) the reversible activation of different phytochromes by red light and their deactivation by far-red light in yeast. Their main model is based on the proteins PhyA and FHL, which have similar properties as PhyB and PIF3 used in E. lemming , as described by the underlying molecular mechanism. In this system, PhyA is fused to the Gal4 bindig domain (GBD) and FHL to the Gal4 transcriptional activator domain. Upon activation with red light, both chimeric proteins bind to each other and the complex can activate the transcription of a lacZ reporter which is under the control of a GAL4-responsive artificial promoter. Upon deactivation with far-red light, the complex dissociates and transcription of the lacZ gene is significantly reduced.

In this model, Sorokina et al assume that PhyA protein sequesteres and only free PhyA can interact with FHL. They state that this interaction is necessary to explain the experimental data presented in the paper, consisting of the strength of fluorescence induced by lacZ over time for different experimental settings. It should be noticed that this signal constantly changes with time in the range of hours.

Implementation

One of the models of system described by Sorokina et al [1] is available in the SBML format [2]. The model was exported to Matlab using SBToolbox2 [3]. However, only the system without input light signals was possible to be reproduced as presented in the paper [1], since the parameters necessary to define these signals were missing.

It was tried to reverse engineer these parameters from the information given in the paper. However, the model available in SBML was slightly different from the model as described in the article: It was not possible to set the strength of the red and far-red light signals directly, but only the derivatives could be adjusted. This modeling decision might have been made to circumvent the problem that some integrators fail to solve a system of differential equations correctly when facing a step change too high in one of the derivatives. To test the model, this work-around was removed and the light inputs were not changed by steps, but by ramps with a length of 1s, which is significant smaller than the other time constants which were relevant for this part of the model. When reproduction of the published data was tried, it was recognized that the strengths of the light signals had to be decreased by approximately 40 fold. Since the exactly inputs of the original simulations were unknown, it was not possible to deduce the reason for this necessary change in the parameters of the model.

Furthermore, several other parameters were not available. These parameters were mainly needed to calculate the fluorescence signal strength from the lacZ concentration. In the paper [1], it was stated that these parameters were obtained for every experiments separatly by fits. To evaluate if the model can reproduce the data in the paper, one of the more important parameters (RLU in [1]) was estimated and the other parameters were set to the standard values from the SBML model, since changes of these parameters had similar effects.

Evaluation of the model

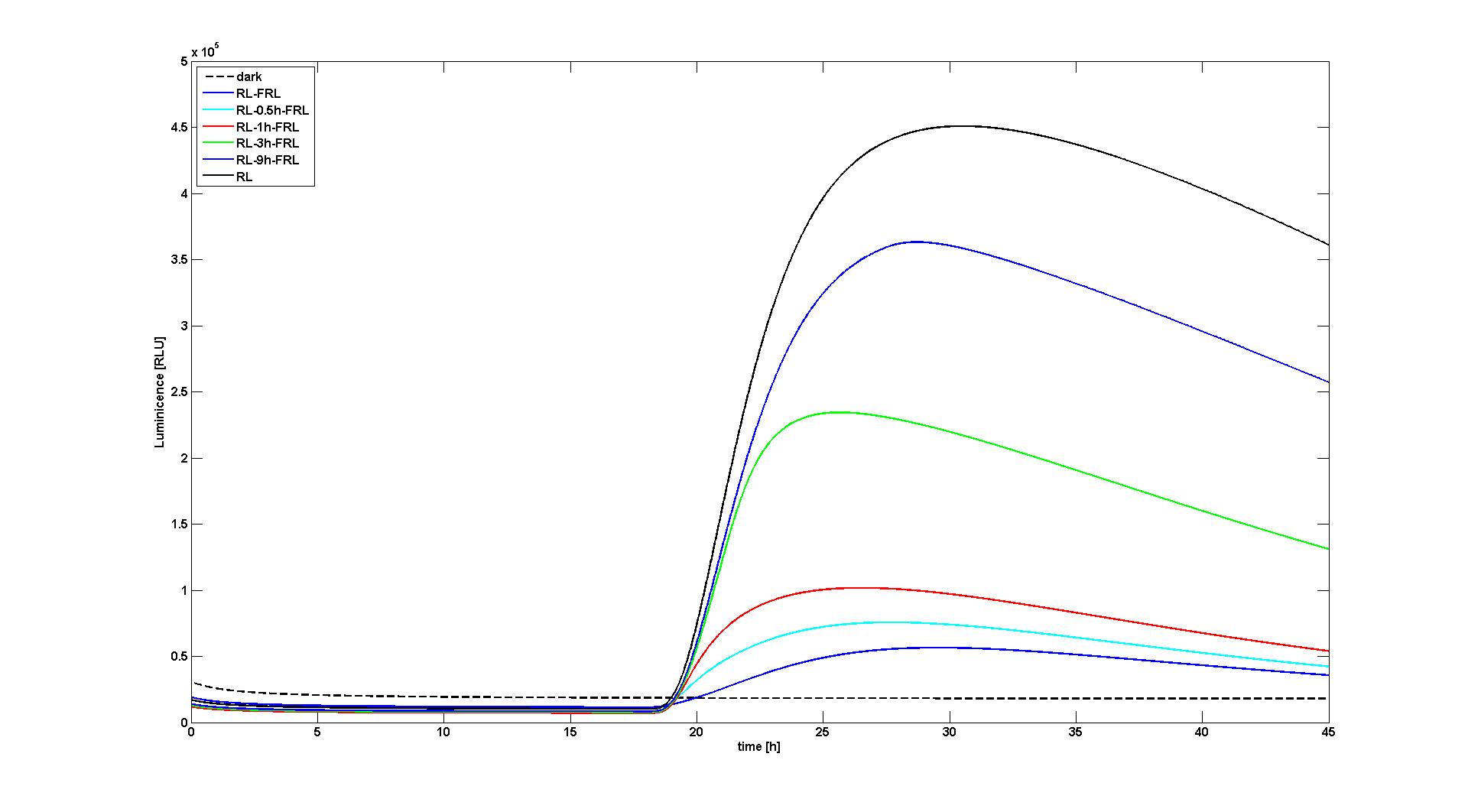Figure 1. Reaction of the model to no light input (dashed black curve), red light for 10 min at t=18h (black curve), red light for 10 min at t=18h followed by a 10min far-red pulse after 0h (blue), 0.5h (cyan), 1h (red), 3h (green), 9h (blue). The values for RLU were set so that the data reproduced the measured data as described by Sorokina et al. This figure corresponds to figure 6A in [1].

Figure 2. Same as Figure 1, only with the same value for RLU for every experiment (set to a value to reproduce Figure 8A in [1]).

With the changes made to the model, it was possible to reproduce the data as presented in the paper. Two of the most significant figures (see Figure 1 and 2) were reproduced, which show the response of the system to different light input signals: Whether to no light input at all (dark), a single red light pulse at t=18h lasting for 10 min, or a 10 min red light pulse at t=18h followed by a 10 min far-red light pulse after 0.5h, 1h, 3h, or 9h. All experiments qualitatively and quantitaively reproduced the simulation results obtained by Sorokina et al (see Figure 6B and Figure 8A in [1]).

References

[1] [http://www.jbioleng.org/content/3/1/15 Sorokina et al: A switchable light-input, light-output system modelled and constructed in yeast. J Biol Eng. 2009 Sep 17;3:15.]

[2] [http://www.biomedcentral.com/content/supplementary/1754-1611-3-15-S3.XML 1754-1611-3-15-S3.XML]

[3] [http://www.sbtoolbox2.org/ SBToolbox2]