Team:ETHZ Basel/InformationProcessing/Controller
From 2010.igem.org
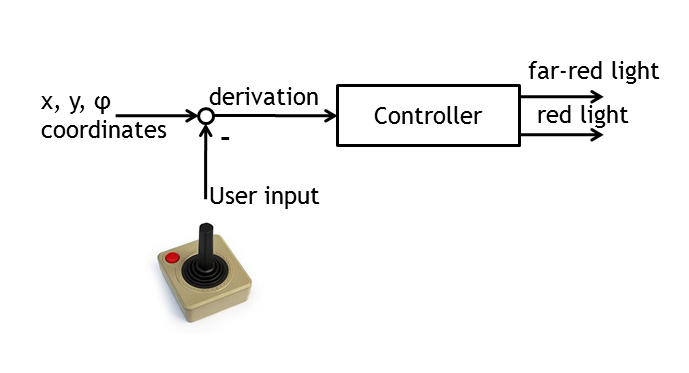
Controller
Introduction
The controller has as inputs the direction the E. lemming is currently swimming and the reverence direction set by the user. The controller algorithm is responsible to induce red and far-red light pulses to minimize the average difference between the two directions. It is executed with the same frequency as images are made in the microscope.Although closed loop controller design is an over 60 years old scientific discipline, some of the properties of the network composed of the in-silico and in-vivo sub-parts, is making this task intractable for most theoretical controller design strategies:
- The chemotaxis network is highly nonlinear.
- Tumbling occurs stochastically.
- The angular change during tumbling is not predictable, neither the direction nor the absolute value.
- During straight swimming the angle is changing stochastically, too (although not as much as during tumbling).
- Microscope, cell detection and tracking, and the approximation of the current angle of the E. lemming sum up to a time delay of approximately one second.
- The approximated angle is highly noisy.
As far as we are aware of, no theoretical controller design algorithm exists that can tackle with all of this challenges. To nevertheless develop several implementations which afterward can be compared in terms of performance, we decided to start a controller design competition between the team members (see next paragraph). Since, due to time restrictions, the controllers had to be developed before the biological assembly of the E. lemming, all controllers were developed on the basis of the model of the E. lemming (one of the several reasons why this model was developed). In the following we first present the rules for the competition, which also include a measure for the performance of a controller, and afterward the different approaches developed by our team members together with their evaluation.
Controller Design Competition
The goal of the competition was to develop an implementation of a controller which performs best in forcing the E. lemming in swimming to a desired direction. Liberally, our instructor Jörg Stelling agreed, more or less voluntarily, to donate a bottle of highly expensive wine as a prize for the winner of the competition.
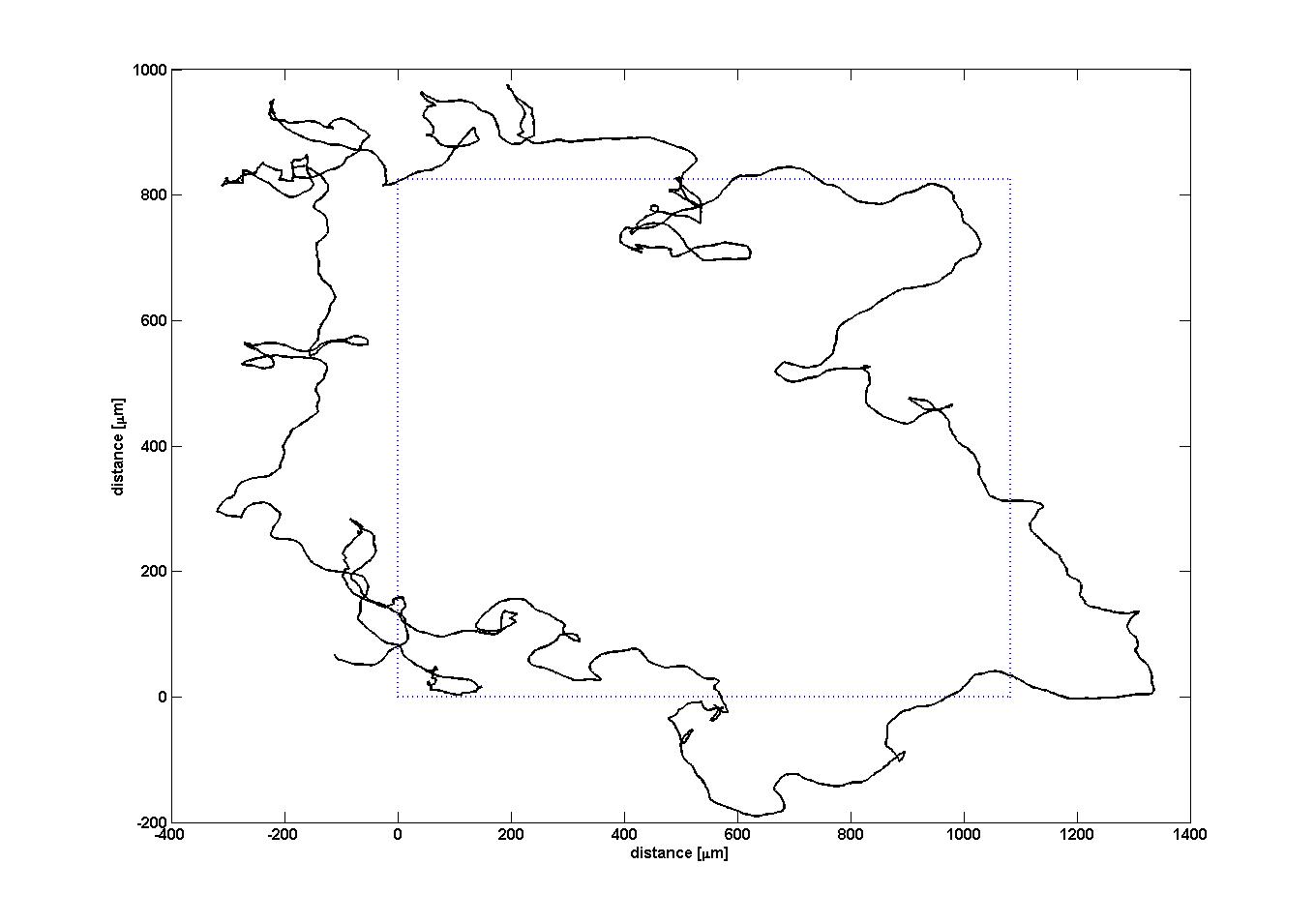
For the competition every participant had to force his or her E. lemming model to swim clockwise around a 1083×825μm large rectangle (approximately the size of 10 microscope images stringed together in each direction). Therefore, the reference direction send to the controller was set in the direction of the next corner of the rectangle. Always when the Euclidean distance between the virtual E. lemming and the active corner was falling below approximately 90μm (approximately the size of one microscope image), the next corner was activated.The current direction of the E. lemming obtained from the model was delayed for 0.9s and white noise was added to simulate the conditions mentioned above. The controller algorithm was called every 0.3s and could either activate or deactivate the red and the far-red light. All other details for the construction of the controllers were left open.
For the evaluation of the controllers we defined the cost function Γ as following:
with T the evaluation time, φis the direction of the E. lemming, φsh the reference direction. The value of the cost function is always ∈[0,2] and can be interpreted as following:
- If Γ=0, the E. lemming would always swim exactly in the reference direction.
- If Γ=2, the E. lemming would always swim exactly opposite to the reference direction.
- A controller which would set the red light and far-red light outputs independent of the current direction of the E. lemming will reach Γ≈1 for T>>1.
The controllers of all participant of the competition were run until the cost function Γ reached approximately a steady state. The participant with the lowest long-time value of his cost function obtained the prize from Jörg. The results are summarized in the following section.
Implemented Controllers
In the following we will list all controllers we implemented ordered increasing by the long-time value of the cost function they achieved. All controllers are nevertheless available in the Lemming Toolbox.
Threshold Optimized Controller (Winner of the Control Design Competition)
Cost function value of Γ=0.7703. Implemented by Simona Constantinescu.
Hysteresis based Sliding Mode Controller
Cost function value of Γ=0.7727. Implemented by Moritz Lang.
|φis-φsh|mod 2π<π/2. However, this decrease can be small for larger differences in this set and especially near the destination a direction of the E. lemming only narrowly fulfilling this condition will soon get invalid due to the movement of the E. lemming nearly tangential to the reference direction. Furthermore, due to the slight changes in direction during swimming and the measurement error when determining the direction of the E. lemming, it can happen that, when the angle between the reference direction and the actual direction is near to π, the direction of the E. lemming "enters" and "leaves" this set very rapidly. A simple algorithm like "red light when the difference of the directions is smaller than π, otherwise far-red light" could then lead to rapid switching between the diodes, an effect not desirable in an experimental setup.
I thus decided to define two sets, Son={φis∈[0,2π):|φis-φsh|mod 2π<π/2} and Soff={φis∈[0,2π):|φis-φsh|mod 2π<π/3}. Furthermore the controller has two states, ζon and ζoff, and the state of the controller is maintained between evaluations of the controller algorithm.
When the controller is in state ζoff, it tests whether φis is in Soff or not. If the condition is fulfilled, a 2.4s (≈4 evaluations) red light pulse is send and the state is set to Son.
When the controller is in state ζon, it tests whether φis is in Son or not. If the condition is not fulfilled, a 2.1s (≈3 evaluations) far-red light pulse is send and the state is set to Soff.
Our evaluations showed that this controller forces the E. lemming successful around the rectangle (see Figure on the right), while minimizing both light pulses.
Noise Refusing Subspace of Trust Controller
Cost function value of Γ=0.8089. Implemented by Christoph Hold.
Four Zones of Preference Controller
Cost function value of Γ=0.8196. Implemented by George Rosenberger.
A core problem of the very simple "red light when the difference of the directions is smaller than π, otherwise far-red light" algorithm is, that the edge between red and far-red light is very sharp. Therefore, the controller often changes between these two states and because of the time delay of the microscope and image processing, prediction of best light pulse tends to be inaccurate at this threshold.
The core concept of this controller is to extend the very basic algorithm in a way, that the edge between red and far-red light is avoided, e.g. it should be leaped. This is achieved by creating a dark area of 2 * 15° between red and far-red thresholds, in which no light pulse is being sent at all. Next to the far-red light zone, the repeating times are increased in an order to possibly leap the dark area and go to a different angle, better (or worse) than the dark area.
Majority Vote Proportional - Second Derivative Threshold Controller
Cost function value of Γ=0.8379. Implemented by Thanuja Ambegoda.
 "
"