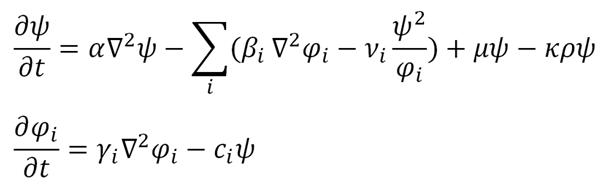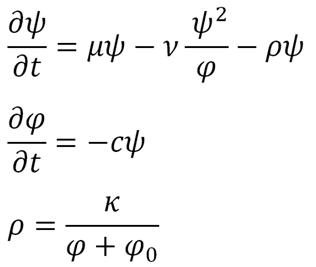Model of bacteria growth and death with killing gene endowed

Generally in the open environment, the population density of bacteriaΨ, the nutrition density φ_i, and the killing signal density ρ can be modeled by the following system of partial differential equation:

With

Where the functional dependence of ρ is to be determined case by case.

Special case

In our project, we assumed a lactose analogue in close environment and homogeneous bacteria culture:

This is a system of two asymptotic equations with environment dependent parameters, which will have to be determined experimentally.

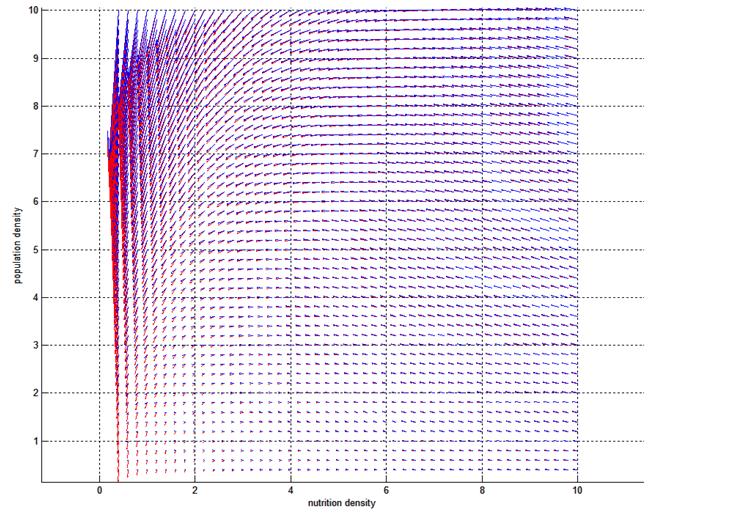
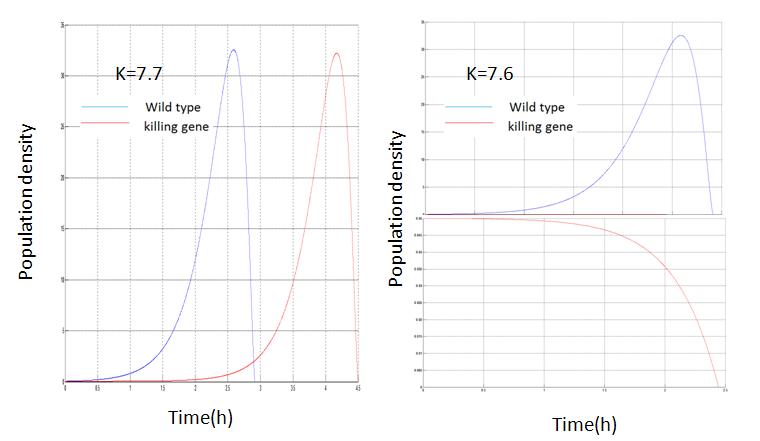
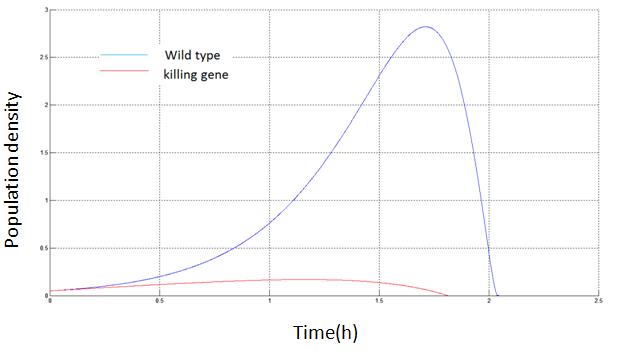
Phase diagram with(blue) and without(red) killing mechanism

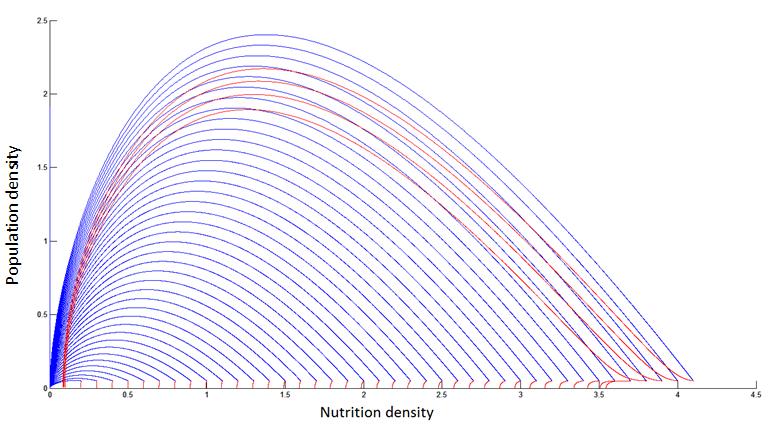
Phase line with(red) and without(blue) killing mechanism

Drastic effects resulted from killing efficiency and initial nutrition density

There is a critical value for killing gene efficiency at a given environment. Below the critical value, the bacteria culture will thrive by suppressing its own survival. Killing a portion of bacteria, the rest will enjoy higher nutrient density for longer time. Above the critical value, the bacteria will kill itself fast enough and hence deprive itself of the chance to take advantage of the death of others.

Remarks

The killing signal should be designed to be independent of the nutrition density.So, if the task of the genetically bacteria has to do with nutrient, as in our lactose analogue, using the nutrient itself as the killing signal is impractical.The idea of a bio-safety net should be further explored with better design of killing signal tailored to the function of the bacterial machinery, for example, time dependent signal.