Team:Groningen/Biofilm model
From 2010.igem.org
Biofilm Dynamics
Introduction
Biofilms are multicellular conglomerates which attach to surfaces. The formation of biofilms is triggered by high cell density and limited resources. The sensing is of these conditions is often mediated by an extracellular signaling compound which increases in concentration and triggers regulating circuitry. This process is called [quorum sensing] and it plays an important role in the dynamics of multicellular systems.
Quorum sensing systems can cause complicated effects including cell differentiation within single species conglomerates. A recent example of this can be seen in the difference of expression in the [http://subtiwiki.uni-goettingen.de/wiki/index.php/TasA TasA protein] which plays a major role in the formation of the biofilm matrix by forming amyloid fibers. Expression of this protein is mediated by competitive inhibitive systems by, amongst others, the [http://subtiwiki.uni-goettingen.de/wiki/index.php/YqxM yqxM gene](<partinfo>BBa_K305006</<partinfo> which linked to the ComXPA quorum sensing system.
However it has been found that not all bacteria respond to the signaling molecules in the same way. It was shown that biofilm formation in Bacillus subtilis involves paracrine signaling in which most cells produce and secrete the signaling molecule ComX but only a sub population of the cells is triggered to make surfactin. Surfactin serves as paracrine signaling molecule and the cells which are not able to make surfactin, respond to surfactin by making extracellular matrix components for the biofilm.
It is hypothesized that the extracellular matrix interferes with the interaction between ComX and the trans membrane histidine kinase ComP and therefore prevents surfactin production in extracellular matrix producing cells. In a mutant which did not express extracellular matrix proteins, the surfactin expression was more than three times higher.
While differentiation requires interaction between several genes and complicated effects as described above we believe even simple extra-cellular accumulation of a pheromone can be responsible.
A very simple model is proposed based on 2D growth of bacteria by cellular automata on a restricted plane. Each of the cells (a pixel in the model) secretes an unnamed compound which is allowed to accumulate. The accumulated compound is diffused at each discrete time step by applying a Gaussian Kernel. Finally at each cell a sigmoidal response curve is mapped, simplifying an all-or-nothing response similar to signal amplification through auto-phosphorylation of transmembrane histidine kinases. Cell differentiation was demonstrated within this theoretical model and variation of the parameters change the response drastically.
Growth by cellular automata
Cellular Automata are discrete computational models. The model consist of a finite grid (of any dimension) in which each of the cells can be in one of a finite set of states. The model behaves discretely in time by evaluating the number of neighbors of each cell and updating its state by some algebraic rule. A popular example of such a model with only two possible states, on and off, and a 2 dimensional grid is Conways Game of life. A possible instantiation of this "game" (it is a zero player game in the sense that it plays itself) is shown below.
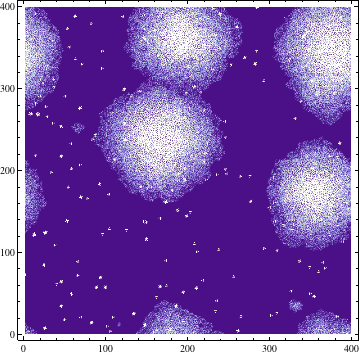
Simpler one dimensional models are an important subject of study in theoretical computer science. We modeled unrestricted bacterial growth by Cellular Automata. The model is a 2D grid of 400x400 pixels, the states are on and off indicating the presence of biomass. The grid is initialized randomly with a fixed distribution of "on" states. At every time step the following rule is applied by evaluating each of the cells 8 neighbors, if a cell has 3 or 4 neighbors with the "on" state the cell itself becomes "on" (a growth step, or birth), if a cell has 4, 5, or 6 neighbors which are on the cell is allowed to live and thus remains on. If any cell does not meet these criteria the cell will remain or become off. An animation of this model is shown below.
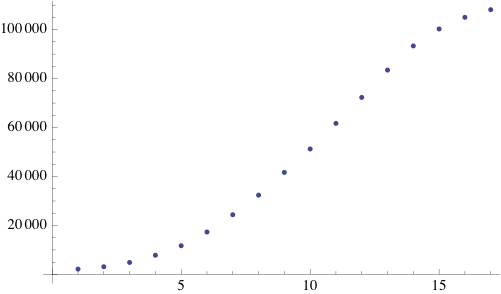
Due to the random initialization the first time steps are trimmed to allow for the distribution to stabilize. The result of the simulation is a binary matrix C for each time step representing biomass occupation. It can be shown by summing the total amount of occupied cell increases exponentially at each step and finally reaching a stationary phase because of spatial limitations.
Quorum sensing pheromones
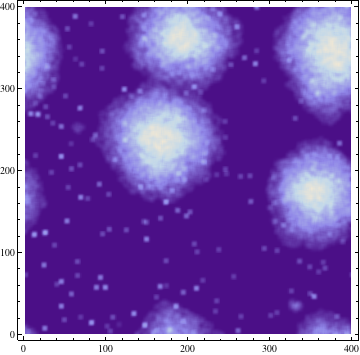
Quorum sensing pheromones are modeled by sampling a random number from the normal distribution for each cell which in on resulting in a new matrix P. Because the sensing pheromones are allowed to accumulate each next time step is the sum of the previous matrices. Quorum sensing requires diffusion of the pheromone from one occupied cell to another. Plotting the density of pheromone gives the following graph:
Continuous diffusion can be modeled using the Heat equation, a two dimensional Partial Differential Equation (PDE) as shown below. Fick's second law is a a common biological and chemical model and is analogous to the two-dimensional Heat equation. This would generate a discrete-differential model.
Solving this equation allows for diffusion continuous in both space and time. However for simplicity we applied a discrete Gaussian filter, equivalent to a convoluting a Gaussian matrix to our substance matrix P generating P'. The Gaussian Filter in 2D has the following form:
Where σ is the standard deviation. The result of this process with σ = 3 is demonstrated at a single time step below:
Activation of genes
Simplification of the Hill kinetics allowed for modeling of gene activation through simple sigmoidal function:
Imputing every element of P' into the function shows which genes are activated. Binarization of the responses allowed to color the activated cells in the original matrix C. Results are discussed below.
Results
The results of the model are shown below in simplified form. Download the interactive code and the [http://www.wolfram.com/products/player/ Mathematica 7 viewer] to play interactively with the model. The cells which have the gene expressed are shown in red.
Future work
The model proposed here is a grave oversimplification and many enhancements can be made. First of all the growth of the biofilm is unrestricted by substance availability Loosdrecht et. al. proposed a more realistic model of biofilm formation taking into account oxygen and substance concentrations. The pheromone is diffused discretely, however a larger resolution would be needed to differentiate between cellular and molecular scale. Implementing the Heat equation would increase the resolution and allow for a more realistic diffusion model. It is now assumed that the pheromone concentrations remain stable over time, however to fully account for its presence substance degradation by extracellular proteins would also need to be modeled.
Also a more realistic model of [gene expression], could be incorporated further increasing its realism by taking into account within-cell dynamics. Also the B.subtilis quorum sensing system does not rely on a single compound, many different molecules diffuse and influence cell behavior. Sporulation for example is known to be a competitive inhibitory system between CSF and ComX.
Sources
The Mathematica 7 source files are available below:
Biofilm model ([http://dl.dropbox.com/u/391356/iGEM/biofilm.nb source])(interactive)
2D Heat equation ([http://dl.dropbox.com/u/391356/iGEM/diff.nb source])
Sigmoid response curve ([http://dl.dropbox.com/u/391356/iGEM/hillSimpl.nb source])([http://dl.dropbox.com/u/391356/iGEM/hillSimpl.nbp interactive])
References
Comella N, Grossman AD, Conservation of genes and processes controlled by the quorum response in bacteria: characterization of genes controlled by the quorum-sensing transcription factor ComA in Bacillus subtilis, Molecular Microbiology (2005), 57 (4): 1159–1174. PMID 16091051
Lemon KP, Earl AM, Vlamakis HC, Aguilar C, Kolter R., Biofilm development with an emphasis on Bacillus subtilis, Current Topics Microbiology and Immunology, 2008, 322:1-16. PMID 18453269
López D, Vlamakis H, Kolter R, Biofilms, Cold Spring Harbor Perspectives in Biology, 2010, (2):a000398. PMID 20519345
López D, Vlamakis H, Losick R, Kolter R, Paracrine signaling in a bacterium, Genes & Development, 2009 23(14):1631-8.
Pérez J, Picioreanu C, van Loosdrecht M, Modeling biofilm and floc diffusion processes based on analytical solution of reaction-diffusion equations, Water Research, 2005, 39:1311-1323.
Picioreanu C, van Loosdrecht MC, Heijnen JJ. A new combined differential-discrete cellular automaton approach for biofilm modeling: application for growth in gel beads, Biotechnology Bioengineering, 1998, 57(6):718-31. PMID 10099251
Picioreanu C, van Loosdrecht MC, Heijnen JJ. Mathematical modeling of biofilm structure with a hybrid differential-discrete cellular automaton approach, Biotechnology Bioengineering, 1998, 58(1):101-16. PMID 10099266 Roggiani M, Dubnau D, ComA, a phosphorylated response regulator protein of Bacillus subtilis, binds to the promoter region of srfA, Journal of Bacteriology, 1993, 175(10): 3182-7. PMID 8387999
Shah IM, Dworkin J, Microbial interactions: bacteria talk to (some of) their neighbors, Current Biology, 2009, 19(16): 689-91. PMID 19706277
 "
"