Team:UT-Tokyo/Sudoku modeling
From 2010.igem.org


Sudoku
Introduction System Modeling Lab note Result Reference
4C3leak switch
We modeled our 4C3 leak switch as deterministic ODE system.
Modelling
Assumption
1.We treated DNA as continuous variabl, since there could be hundreds of plasmid in one E.coli (multicopy plasmid). There are 32 kinds of variables that stand for DNA concentration corresponding to their different internal states.
2.We assumed that cre recombinase operate as tetramer, and other recombinase as dimer (but this seems not to be relevant).
3.We assumed that association and dissociation of DNA recombinase to DNA is sufficiently fast so that equilibrate in the timescale of the whole switch.
4.We ignored the reverse reaction of DNA recombinase because we used irreversible sequence (lox66, lox71 etc).
Variable
Basically, "pn" denotes for protein concentration and "rn" denotes for mRNA concentration
p1,p2,p3,p4 : concentration of 4 recombinase protein
r1,r2,r3,r4 : concentration of 4 recombinass mRNA
u1,u2,u3,u4 : concentration of input mRNA
pc,rc : concentration of cre recombinase protein and mRNA
ps,rs : concentration of SP6 polymerase protein and mRNA
Parameters
k0 : mRNA translation rate
k1 : protein degradation rate
k2 : mRNA translation rate
k3 : cre protein degradation rate
l0 : transcription speed per unit concentration of RNA polymearase
l1 : mRNA degradation rate
l2 : cre mRNA degradation rate
K : recombinase binding constant
v : recombinase reaction rate
pT7 : concentration o T7 polymerase
p : terminator leak probability
Equations
Methods
We used our original python program (4 th order explicit Runge-Kutta algorithm) to solve thess equations.
Results
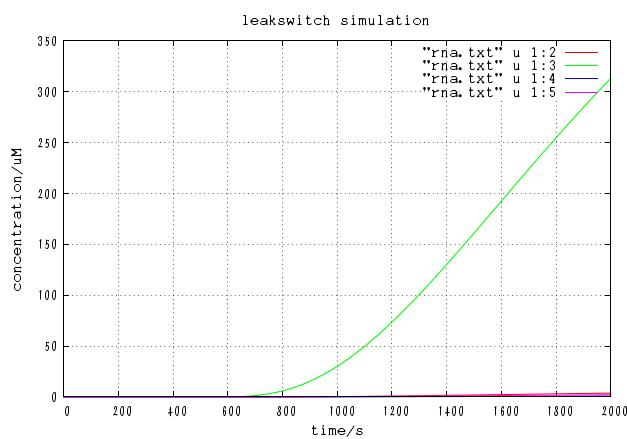
The time course of DNA concentration
The time course of mRNA concentration. Note that the output of this system is not protein but mRNA.
Discussion
It is confirmed that the system works as expected with a certain combination of parameters.
In addition, we changed many parameters, especially,l0,v(whose values are unclear) and p(leakiness of terminator) , to see whether the device is able to operate within a large part of parameter space.
As a result, the circuit can function correctly within the range of 0.001< p < 0.1, 0.001 < v <1.0, 0.01 < l0 < 1.0 , demonstrating its robustness.
conclusion
MS2 phage infection
Whole system
 "
"