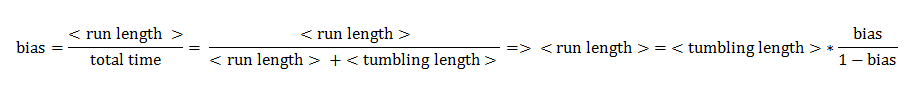"

From 2010.igem.org

Modeling & Simulating Bacterial Movement

While the biologists are busy teaching the E. coli how to respond to light, the modelers thought of simulating the light driven E. coli electronically. This will close the loop of our virtual E.lemming and will help us check the imaging pipeline, microscope analysis & joystick control even without actually having the real E. lemming under the microscope.

Overview

Analogous to the highly complex signal transduction in the Chemotaxis receptor model, there is an equally challenging molecular mechanism on side of the flagella, responsible for the movement of the bacterium.
In order to capture the realistic features of cell motility under Chemotaxis, we implemented a probabilistic model, which performs in accordance to the existing empirical observations on Chemotaxis movement. At every time point of the simulation, CheYp concentration is received as an input from the Chemotaxis pathway model. This input determines whether, in the next time point, the flagella will rotate counterclockise (pushing the cell forward) or clockwise (changing its direction of movement).
The coupling of the probabilistic movement model with the molecular model ensures that we can realistically simulate the variations in the motility with the variations in the protein concentrations.

Concepts

The main concepts we used in deriving and implementing our model are based on the most important features observed in the real behavior of E.coli. These features are:

The Bias

The link between CheYp concentration and the type of movement chosen by the bacterium is called bias and it is formally defined as the fraction of time spent in the running state with respect to the total observation time. Our choice for bias formulation was a nonlinear Hill - type function of the CheYp concentration, with one of the parameters being the wild - type CheYp concentration for which a steady - state bias value was obtained. Both the functional dependency and CheYp value are well documented from the literature side [2].

At every time point of the simulation, the cell probabilistically chooses whether to run or to tumble, depending on the bias value. The choice of the running state is equivalent to a change in spatial coordinates, together with a slight change in direction (movement angle), while the choice of the tumbling state corresponds to new movement angle and unchanged spatial coordinates.

Mean times

An important way of characterizing the cell's behavior is by statistically observing it over a longer time period.
From this aspect, the mean tumbling length is the average time the cell spends in between two runs, while the mean run length is the average time spent in the running state.

Tumbling angle

The tumbling angle is the change of direction from run to run. We approximated the empirically observed distribution with a Weibull distribution (right panel), with same mean and variance as the empirically observed ones.

The Algorithm

We use a two state model that reflects the two states the cell can be in through out its motion - swimming state & the tumbling state. At each time-step of the simulation, the cell will either stay in the same state or will switch the state according to these probabilities. Details of these probability values can be found below.

Transition Probabilities

In each of these states, there is a transition probability to switch to the other states. As described below, we have the probability P1 that tells us the probability of switching to the tumbling state when the cell is currently in the swimming state and also the probability P2 that that reflects the probability of switching to the running state

Assumptions

The assumptions of our model were taken in accordance to the existing empirical data on the chemotaxis movement [1]. The mean tumbling length is assumed to be constant, unlike the mean running length, which is a function of the bias. Besides the experimental evidence, this assumption also has an intuitive meaning: the running probability doesn't influence the amount of time the cell spends in the tumbling state, whereas it matters when deciding the next move, if the cell already is in the running state. Also, the mean velocity during runs was considered constant.

Features of the Movement Model

One of the biggest challenges regarding the movement model was obtaining a time - step - invariant behavior of the cell, whose reliability of statistical estimates should be the same, regardless of how often the cell had to choose its future state. In order to achieve this, we opted for a two - state model, in which the probability of running was controlled separately depending on whether the cell was running or tumbling.
Therefore the two central parameters of our model are the probability of keeping the current state in the next time interval: probability of future state being running, when the current state is running (p1) and probability of the future state being tumbling, when the current state is tumbling (p2).
In deriving the expression of these probabilities, we separately and symmetrically focused on the two processes: running and tumbling. As a consequence, the mean running length is only dependent on the timestep and on the probability of continuing running (p1), while the mean tumbling length is only dependent on the time - step and on the probability of continuing tumbling, if the previous step was tumbling (p2).
We will explain in detail the technique employed in deriving the probability of running, when the previous state was running. The symmetrical calculations, for the mean tumbling length, follow identically.

The mean running length is the expected value of a random variable representing the number of timesteps the cell consecutively spends in running. By expanding the definition of an expected value, the mean running length becomes an infinite sum over all possible consecutive running-lengths, multiplied by their respective occurrence probabilities.

[1] Chemotaxis in Escherichia coli analysed by three - dimensional Tracking. H.C. Berg, D.A.Brown: Nature 239, 500 - 504. 1972
[2] Levin, Morton-Firth (1998), "Origins of Individual Swimming Behavior in Bacteria", Biophysical Journal 74:175-181