Team:ETHZ Basel/Modeling/Movement

From 2010.igem.org

(Difference between revisions)
(→Modeling of the bacterial movement)
Line 3: Line 3:
= Modeling of the bacterial movement =
= Modeling of the bacterial movement =
 +
 +
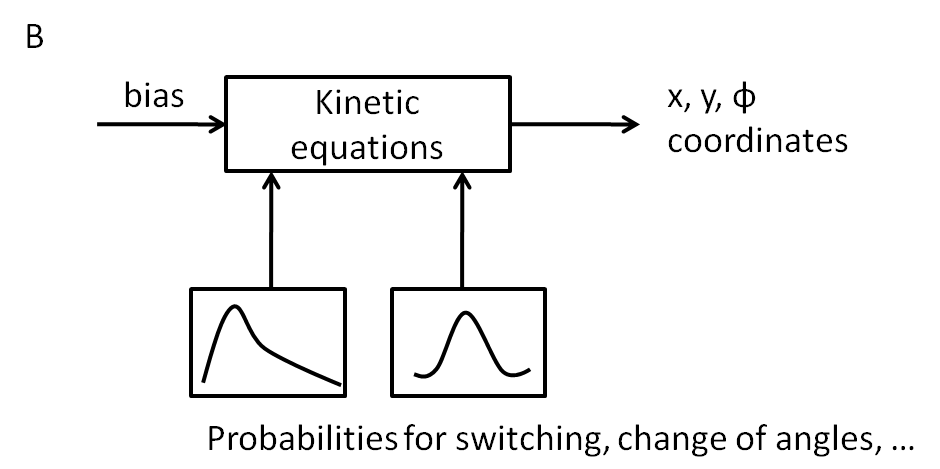
For simulating the movement of E.coli, we implemented a probabilistic model, meant to reproduce the main statistical features of the existing empirical data. At every time point of the simulation, CheYp concentration is received as an input from the molecular model of the Chemotaxis pathway. From the already - known CheYp - CCW movement dependence (or bias), the probability of CCW movement (running) for the given CheYp concentration and for the given time - point is obtained. The cell then probabilistically chooses whether to run or to tumble. The choice of the running state is equivalent to a change in spatial coordinates, but not in the movement angle, while the choice of the tumbling state corresponds to new movement angle and unchanged spatial coordinates. During tumbling, the change in angle is sampled from a Gaussian distribution, with mean and variance documented from the literature.
 +
 +
The dependence CheYp - running probability was obtained from the literature:
 +
 +
 +
 +
 
 +
 +
 +
[[Image:ETHZ_Basel_molecular_move.png|thumb|400px|'''Schematical overview of the relation between chemotaxis and the movement model.''']]
[[Image:ETHZ_Basel_molecular_move.png|thumb|400px|'''Schematical overview of the relation between chemotaxis and the movement model.''']]
Line 9: Line 20:
[[Image:B1.png|center|600px|Sketch for a possible implementation of the controller.]]
[[Image:B1.png|center|600px|Sketch for a possible implementation of the controller.]]
-
Analogous to the highly complex signal transduction in chemotaxis there is an equally extensive system on side of the flagella, which is even lower understood. As the movement model is only set up in order to close the feedback chain for testing purposes, a phenomenological implementation will be sufficient. <br>
+
Analogous to the highly complex signal transduction in chemotaxis, there is an equally extensive system on side of the flagella, which is even less understood. <br>
Brief descriptions about the statistics of ''E. coli'' movement can be found in the [https://2010.igem.org/Team:ETHZ_Basel/Literature#Movement_statistics literature section] and therefore the model will be a stochastical one.
Brief descriptions about the statistics of ''E. coli'' movement can be found in the [https://2010.igem.org/Team:ETHZ_Basel/Literature#Movement_statistics literature section] and therefore the model will be a stochastical one.
<br><br>
<br><br>

Revision as of 18:41, 10 October 2010

Modeling of the bacterial movement

For simulating the movement of E.coli, we implemented a probabilistic model, meant to reproduce the main statistical features of the existing empirical data. At every time point of the simulation, CheYp concentration is received as an input from the molecular model of the Chemotaxis pathway. From the already - known CheYp - CCW movement dependence (or bias), the probability of CCW movement (running) for the given CheYp concentration and for the given time - point is obtained. The cell then probabilistically chooses whether to run or to tumble. The choice of the running state is equivalent to a change in spatial coordinates, but not in the movement angle, while the choice of the tumbling state corresponds to new movement angle and unchanged spatial coordinates. During tumbling, the change in angle is sampled from a Gaussian distribution, with mean and variance documented from the literature.

The dependence CheYp - running probability was obtained from the literature:




Schematical overview of the relation between chemotaxis and the movement model.
1000$
BACTERIAL ARTWORK FOR SALE
Sketch for a possible implementation of the controller.

Analogous to the highly complex signal transduction in chemotaxis, there is an equally extensive system on side of the flagella, which is even less understood.
Brief descriptions about the statistics of E. coli movement can be found in the literature section and therefore the model will be a stochastical one.

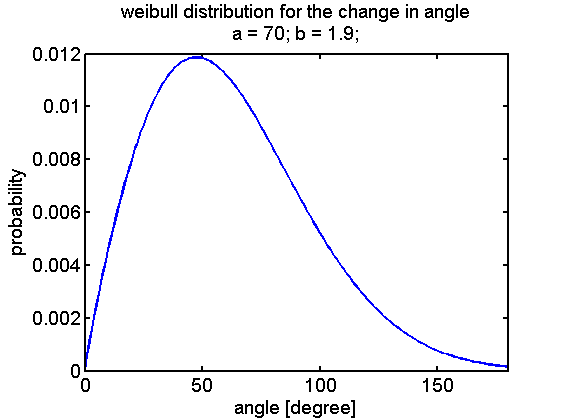
A first implementation was performed by linking the CheYp concentration to the probability of being in the run or tumbling state. These two states either describe the movement and the reorientation as difference equations that can be evaluated at discrete time points. Based on literature statistics about the distribution of change in angle due to tumbling a weibull distribution was selected:

Chosen weibull distribution.

To represent the probability density function it is transformed into a vector that has a frequency of elements that corresponds to the relation of probabilities of the function.

Frequency of elements in the vector.

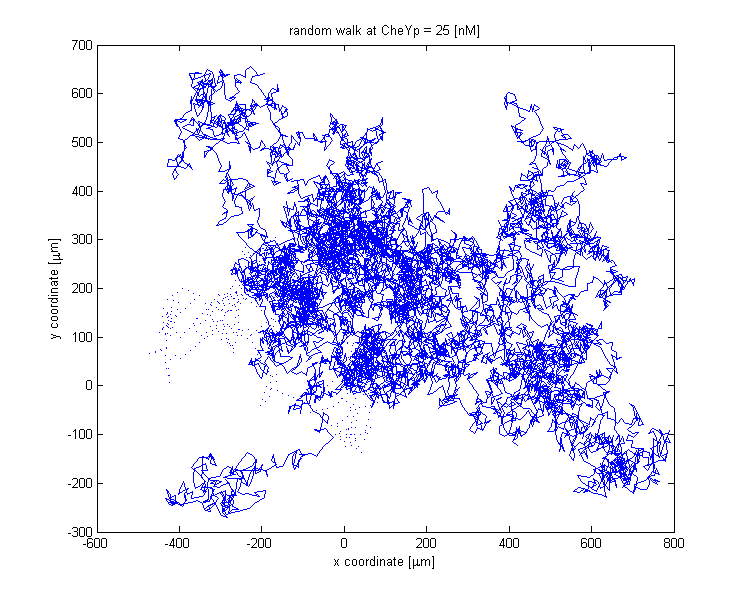
The reorientation happens by selecting a random element of the vector giving the new change in angle. The walks for a thousand steps at different constant CheYp concentrations are shown below:
At a CheYp concentration of 0 the probability for running is about 98%.

A random walk at CheYp = 0 [nM].

At CheYp = 12.5 [nM] both states are equally probable.

A random walk at CheYp = 12.5 [nM].

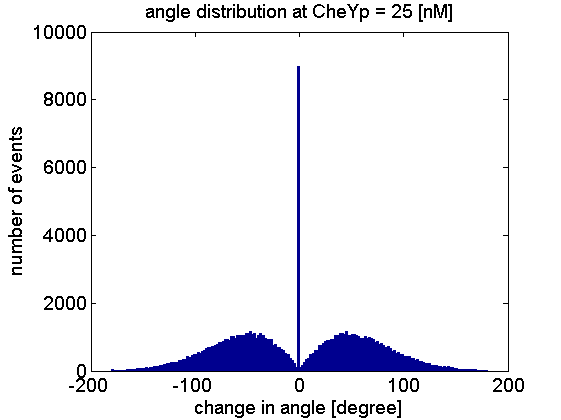
At CheYp = 25 [nM] tumbling is dominant.

A random walk at CheYp = 25 [nM].

Here is the check of change of angele at 25 [nM] for 1e5 steps:

Check of angle distribution.
Retrieved from "http://2010.igem.org/Team:ETHZ_Basel/Modeling/Movement"