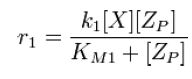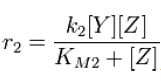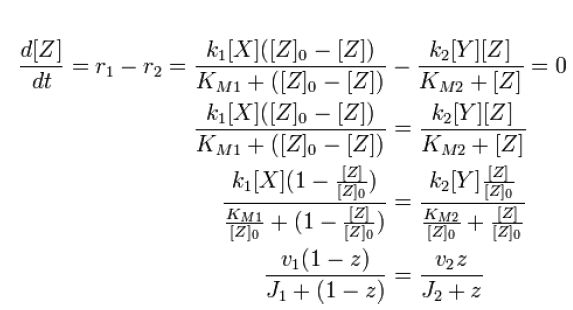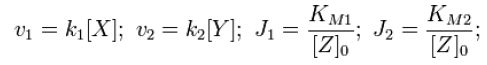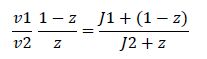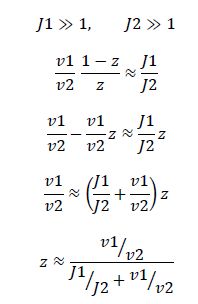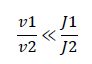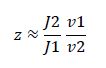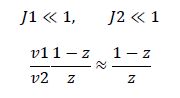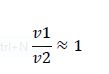Team:Stanford/Research/Modeling

From 2010.igem.org

(Difference between revisions)
(→Kinase/Phosphatase System)
(→Kinase/Phosphatase System)
Line 451: Line 451:
From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is  
From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is  
-
[[Image:R1.JPG]][[Team:Stanford/Research/Modeling/#References| [1]]]
+
[[Image:R1.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
and the rate at which Z is phosphorylated is  
and the rate at which Z is phosphorylated is  
-
[[Image:R2.JPG]][[Team:Stanford/Research/Modeling/#References| [1]]]
+
[[Image:R2.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
We also know that Z can be modified an unmodified, but its total is conserved: [Z]o = [Zp] + [Z]
We also know that Z can be modified an unmodified, but its total is conserved: [Z]o = [Zp] + [Z]
Line 461: Line 461:
At steady state, modification and unmodification rates are equal, leading us to
At steady state, modification and unmodification rates are equal, leading us to
-
[[Image:1stblock.JPG]][[Team:Stanford/Research/Modeling/#References| [1]]]
+
[[Image:1stblock.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]
where
where
-
[[Image:2nd_block.JPG]][Team:Stanford/Research/Modeling/#References| [2]]]
+
[[Image:2nd_block.JPG]][[Team:Stanford/Research/Modeling#References| [2]]]

Revision as of 02:24, 28 October 2010

Home Project Applications Modeling Parts Team Notebook Twitter

Contents

Goals

Our intuition for what makes a good ratio sensor could only take us so far. From the very first stages of design, we wanted to back up and test our ideas with mathematical tools. Luckily, we found that solving the equations of mass action kinetics at steady-state was enough to give us clear design criteria. We present the mathematical basis for sensors that are capable of sensing a single ratio digitally, or many ratios in an analog fashion.

The System

sRNA System

Boolean model for the sRNA system. This is mean to provide a significantly simplified mathematical understanding of the dynamics involved.

iGEM_boolean_sRNA_model

clear all
clc

%Constants and Values
trackingNum = 6;    %mRNA_pA, mRNA_pB, sRNA_A, sRNA_B, protein_A, protein_B;
inputNum = 2;       %A, B;
processNum = 6;     %Trx_pA, Trx_sRNA_A, Trx_pB, Trx_sRNA_B, Trl_A, Trl_B;

%Cell/Matrix Dimensions
m = 2^trackingNum;
n = 2^inputNum;
c = cell(m+1, n+1);

trackingMatrix = de2bi(0:m-1);
inputMatrix = de2bi(0:n-1);
processMatrix = zeros(1,processNum);

%Populating the Cell (Tracking x Input)
c{1,1} = [0];
for j = 1
    for i = 2:m+1
        c{i,j} = trackingMatrix(i-1,:);
    end
end
for i = 1
    for j = 2:n+1
        c{i,j} = inputMatrix(j-1,:);
    end
end
for i = 2:m+1
    for j = 2:n+1
        c{i,j} = processMatrix;
    end
end

%Rules, Acessing, and Changing
for j = 2:n+1
    A = c{1,j}(1);
    B = c{1,j}(2);

    for i = 2:m+1
        mRNA_pA = c{i,1}(1);
        mRNA_pB = c{i,1}(2);
        sRNA_A = c{i,1}(3);
        sRNA_B = c{i,1}(4);
        protein_A = c{i,1}(5);
        protein_B = c{i,1}(6);

        %Trx_pA
        if A == 1
            c{i,j}(1) = 1;
        end

        %Trx_pB
        if B == 1
            c{i,j}(2) = 1;
        end

        %Trx_sRNA_A
        if A == 1
            c{i,j}(3) = 1;
        end

        %Trx_sRNA_B
        if B == 1
            c{i,j}(4) = 1;
        end

        %Trl_A
        if mRNA_pA == 1 && mRNA_pB == 0
            c{i,j}(5) = 1;
        end

        %Trl_B
        if mRNA_pB == 1 && mRNA_pA == 0
            c{i,j}(6) = 1;
        end

    end
end

%Display Results (Column by Column)
[nrows,ncols]= size(c);
%Condense Cell and Display
for i = 1:nrows
    for j = 1:ncols
        string = num2str(c{i,j});
        l = length(string);
        r = 1;
        s = 1;
        t = 0;

        while t ~= 1
            if r == l
            t = 1;
            end

            noSpacesString(s) = string(r);
            r = r+3;
            s = s+1;
        end
        c{i,j} = noSpacesString;
    end
end
c(:,:)

%Find Steady States and Corresponding Inputs
counter = 1;
for i = 2:m+1
    for j = 2:n+1
        if c{i,j} == c{i,1}
            completeMatrix{counter,1} = c{i,j};             %Steady state values
            completeMatrix{counter,2} = num2str([i-1,j-1]); %Location (n x m) within results area
            completeMatrix{counter,3} = c{1,j};             %Corresponding input values
            counter = counter+1;
        end
    end
end
SS_mXn_Input = completeMatrix

time = 0:processNum;
%plot(time,,time,,time,,time,,time,,time,)

%New Cell for Specific Cases
% d(:,1) = c(:,1);
% for j = 2:n+1
%     C1 = '0000';
%     C2 = '0011';
%     C3 = '0100';
%     C4 = '0111';
%     C5 = '1000';
%     C6 = '1011';
%     C7 = '1100';
%
%     a = {C1, C2, C3, C4, C5, C6, C7};
%     for b = 1:1:length(a)
%         if strcmp(c(1,j),a(b)) == 1
%             d(:,b+1) = c(:,j);
%         end
%     end
% end
% d

ans = 

    '0'         '00'        '01'        '10'        '11'    
    '000000'    '000000'    '010100'    '101000'    '111100'
    '000001'    '000000'    '010100'    '101000'    '111100'
    '000010'    '000000'    '010100'    '101000'    '111100'
    '000011'    '000000'    '010100'    '101000'    '111100'
    '000100'    '000000'    '010100'    '101000'    '111100'
    '000101'    '000000'    '010100'    '101000'    '111100'
    '000110'    '000000'    '010100'    '101000'    '111100'
    '000111'    '000000'    '010100'    '101000'    '111100'
    '001000'    '000000'    '010100'    '101000'    '111100'
    '001001'    '000000'    '010100'    '101000'    '111100'
    '001010'    '000000'    '010100'    '101000'    '111100'
    '001011'    '000000'    '010100'    '101000'    '111100'
    '001100'    '000000'    '010100'    '101000'    '111100'
    '001101'    '000000'    '010100'    '101000'    '111100'
    '001110'    '000000'    '010100'    '101000'    '111100'
    '001111'    '000000'    '010100'    '101000'    '111100'
    '010000'    '000001'    '010101'    '101001'    '111101'
    '010001'    '000001'    '010101'    '101001'    '111101'
    '010010'    '000001'    '010101'    '101001'    '111101'
    '010011'    '000001'    '010101'    '101001'    '111101'
    '010100'    '000001'    '010101'    '101001'    '111101'
    '010101'    '000001'    '010101'    '101001'    '111101'
    '010110'    '000001'    '010101'    '101001'    '111101'
    '010111'    '000001'    '010101'    '101001'    '111101'
    '011000'    '000001'    '010101'    '101001'    '111101'
    '011001'    '000001'    '010101'    '101001'    '111101'
    '011010'    '000001'    '010101'    '101001'    '111101'
    '011011'    '000001'    '010101'    '101001'    '111101'
    '011100'    '000001'    '010101'    '101001'    '111101'
    '011101'    '000001'    '010101'    '101001'    '111101'
    '011110'    '000001'    '010101'    '101001'    '111101'
    '011111'    '000001'    '010101'    '101001'    '111101'
    '100000'    '000010'    '010110'    '101010'    '111110'
    '100001'    '000010'    '010110'    '101010'    '111110'
    '100010'    '000010'    '010110'    '101010'    '111110'
    '100011'    '000010'    '010110'    '101010'    '111110'
    '100100'    '000010'    '010110'    '101010'    '111110'
    '100101'    '000010'    '010110'    '101010'    '111110'
    '100110'    '000010'    '010110'    '101010'    '111110'
    '100111'    '000010'    '010110'    '101010'    '111110'
    '101000'    '000010'    '010110'    '101010'    '111110'
    '101001'    '000010'    '010110'    '101010'    '111110'
    '101010'    '000010'    '010110'    '101010'    '111110'
    '101011'    '000010'    '010110'    '101010'    '111110'
    '101100'    '000010'    '010110'    '101010'    '111110'
    '101101'    '000010'    '010110'    '101010'    '111110'
    '101110'    '000010'    '010110'    '101010'    '111110'
    '101111'    '000010'    '010110'    '101010'    '111110'
    '110000'    '000000'    '010100'    '101000'    '111100'
    '110001'    '000000'    '010100'    '101000'    '111100'
    '110010'    '000000'    '010100'    '101000'    '111100'
    '110011'    '000000'    '010100'    '101000'    '111100'
    '110100'    '000000'    '010100'    '101000'    '111100'
    '110101'    '000000'    '010100'    '101000'    '111100'
    '110110'    '000000'    '010100'    '101000'    '111100'
    '110111'    '000000'    '010100'    '101000'    '111100'
    '111000'    '000000'    '010100'    '101000'    '111100'
    '111001'    '000000'    '010100'    '101000'    '111100'
    '111010'    '000000'    '010100'    '101000'    '111100'
    '111011'    '000000'    '010100'    '101000'    '111100'
    '111100'    '000000'    '010100'    '101000'    '111100'
    '111101'    '000000'    '010100'    '101000'    '111100'
    '111110'    '000000'    '010100'    '101000'    '111100'
    '111111'    '000000'    '010100'    '101000'    '111100'


SS_mXn_Input = 

    '000000'    '1  1'      '00'
    '010101'    '22   2'    '01'
    '101010'    '43   3'    '10'
    '111100'    '61   4'    '11'


Published with MATLAB® 7.10


Kinase/Phosphatase System

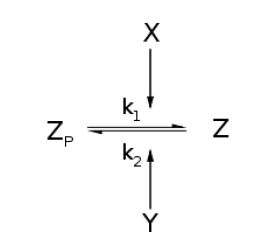
Throughout this derivation, we refer to Goldbeter and Koshland's seminal work on the kinetics of emzyme pairs [1]. For an opposing pair of enzymes X and Y modifying and unmodifying a substrate Z with modification p, MainGBK.JPG

From Michaelis-Menten kinetics we know that the rate at which Zp is dephosphorylated is

R1.JPG [2]

and the rate at which Z is phosphorylated is

R2.JPG [2]

We also know that Z can be modified an unmodified, but its total is conserved: [Z]o = [Zp] + [Z]

At steady state, modification and unmodification rates are equal, leading us to

1stblock.JPG [2]

where

2nd block.JPG [2]


Rearranging gives

3rdblock.JPG.

Now, assume that the two opposing enzymes are nowhere near being saturated with substrate:

4thblock.JPG

So, the fraction of modified substrate is a saturating function of the ratio of inputs. The half-max value is the ratio of the strengths of the two enzymes. The linear regime of this function exists where

5thblock.JPG,

and the fraction of unmodified substrate is a linear function of the ratio of inputs.

6thblock.JPG

We now know that the requirements for this analog ratio sensor are

  1. Consistent relationships between inputs and enzyme activities (non-trivial)
  2. A non-saturating amount of substrate

But what happens if we disobey requirement 1? Let's increase the amount of substrate to saturation so that

7thblock.JPG

8thblock.JPG

When the enzymes are saturated, the only steady-state solution is v1 = v2. Any ratio of v1/v2 below this, and all the substrate becomes modified. Any ratio above and all the substrate becomes unmodified. Simply by changing the concentration of substrate, we have converted our analog ratio sensor to a digital ratio sensor.

The requirements for this digital ratio sensor are:

  1. Consistent relationships between inputs and enzyme activities (non-trivial)
  2. An amount of substrate sufficient to saturate both opposing enzymes

References

[1] [http://www.ncbi.nlm.nih.gov/pubmed/6947258 Goldbeter A, Koshland DE Jr.: An amplified sensitivity arising from covalent modification in biological systems. PNAS. 1981 Nov;78(11)6840-4.]

[2] [http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics Goldbeter-Koshland kinetics In Wikipedia. Retrieved July 13, 2010, from http://en.wikipedia.org/wiki/Goldbeter-Koshland_kinetics]

Retrieved from "http://2010.igem.org/Team:Stanford/Research/Modeling"