Team:Peking/Modeling
From 2010.igem.org
Evamonlight (Talk | contribs) (→References) |
(→Introduction) |
||
| Line 18: | Line 18: | ||
</html> | </html> | ||
=Introduction= | =Introduction= | ||
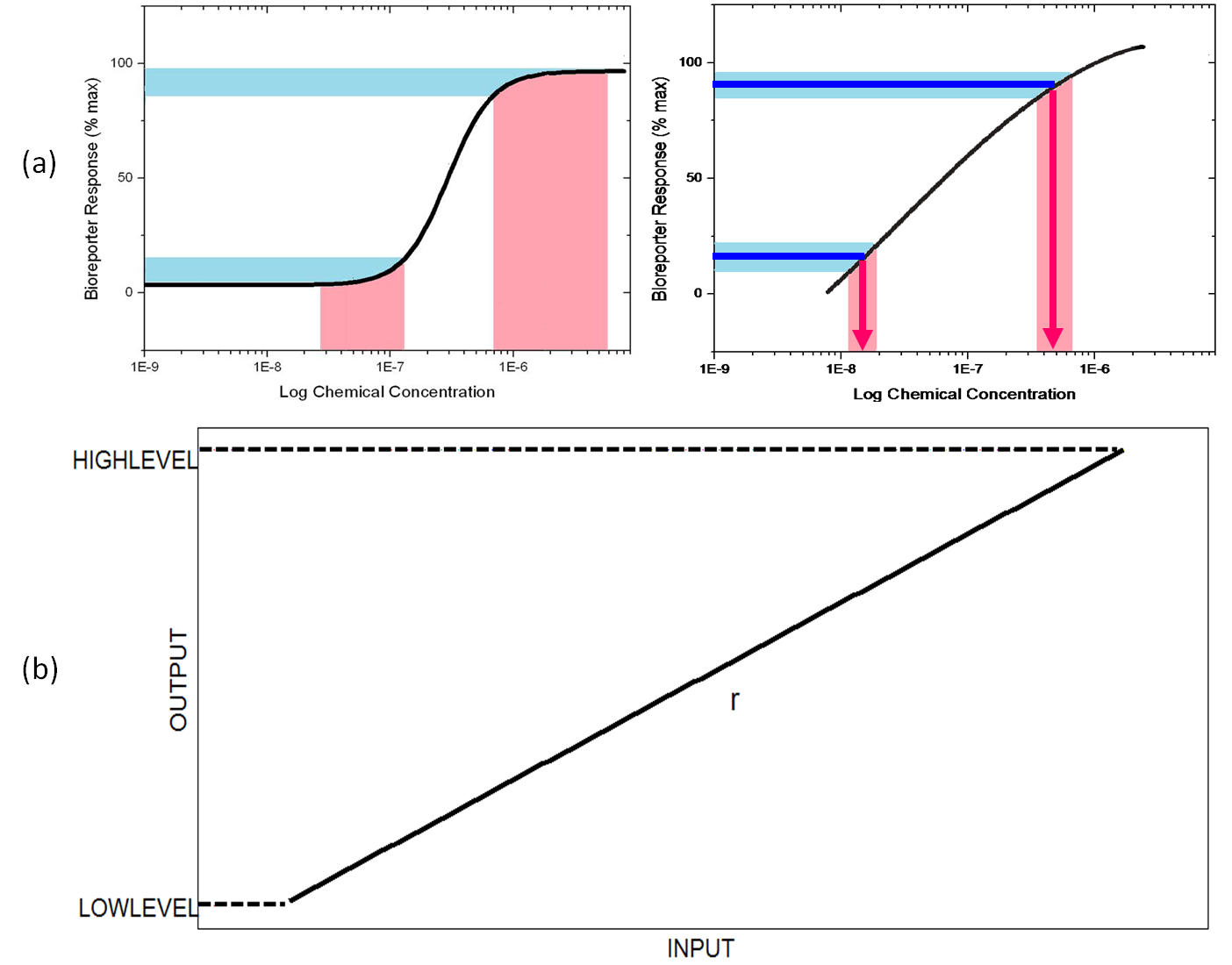
| - | The biological systems are full of noises, and the response of bioreporters | + | The biological systems are full of noises, and the response of bioreporters can be represented by a Hill Function. Noises will be significantly amplified and the output detected will be invalid at the ends of dose response curve.(Figure 1(a)) Therefore, The detection is limited at a narrow range. In order to solve the problem, we seek to transform the Hill Function curve to a straight line. As Figure 1(a) shows, the noise is reducted, and the sensitivity and detectable-range-characteristic of biosensors will be significantly improved. <br><br> |
Aimed at finding a genetic circuit that can perform the transformation, a simple and universal one for practice convenience, we adopted the process of [[Team:Peking/Notebook/Vocabulary#Reverse engineering|Reverse engineering]] which in our work means to enumerate all possible networks and analyzed whether they function well, thus getting the right topology. In details, we first express the target functionalities in quantitative characters and set numerical standards according to our expectations, next define the network for simplest circuit search and derive equations precisely describing it, then calculate the characters using the equations and compare them with standards, then further analyze the comparison results and find the simplest functional network. Finally, to fully understand it and provide enough information for application, we analyze the mechanism and the parameter preferences, as well as exploring whether the very circuit is necessary for performing the function well. | Aimed at finding a genetic circuit that can perform the transformation, a simple and universal one for practice convenience, we adopted the process of [[Team:Peking/Notebook/Vocabulary#Reverse engineering|Reverse engineering]] which in our work means to enumerate all possible networks and analyzed whether they function well, thus getting the right topology. In details, we first express the target functionalities in quantitative characters and set numerical standards according to our expectations, next define the network for simplest circuit search and derive equations precisely describing it, then calculate the characters using the equations and compare them with standards, then further analyze the comparison results and find the simplest functional network. Finally, to fully understand it and provide enough information for application, we analyze the mechanism and the parameter preferences, as well as exploring whether the very circuit is necessary for performing the function well. | ||
<br><br> | <br><br> | ||
Latest revision as of 02:22, 28 October 2010

Modeling Home
Introduction
The biological systems are full of noises, and the response of bioreporters can be represented by a Hill Function. Noises will be significantly amplified and the output detected will be invalid at the ends of dose response curve.(Figure 1(a)) Therefore, The detection is limited at a narrow range. In order to solve the problem, we seek to transform the Hill Function curve to a straight line. As Figure 1(a) shows, the noise is reducted, and the sensitivity and detectable-range-characteristic of biosensors will be significantly improved.
Aimed at finding a genetic circuit that can perform the transformation, a simple and universal one for practice convenience, we adopted the process of Reverse engineering which in our work means to enumerate all possible networks and analyzed whether they function well, thus getting the right topology. In details, we first express the target functionalities in quantitative characters and set numerical standards according to our expectations, next define the network for simplest circuit search and derive equations precisely describing it, then calculate the characters using the equations and compare them with standards, then further analyze the comparison results and find the simplest functional network. Finally, to fully understand it and provide enough information for application, we analyze the mechanism and the parameter preferences, as well as exploring whether the very circuit is necessary for performing the function well.
Here we name our target functionality as Input-Output Alignment(IOA). In order to define IOA precisely for need of calculation, we considered most important characters of IOA and adopted Pearson Correlation Coefficient r to represent Input-Output Linear Relationship in the overall search work ( when r>0.99 we consider the network topology having the IOA function ), and also, regulated two levels for the initial and ultimate output concentration for the second character – the output range in further search work.(Figure 1(b))
Figure 1 (a) The transformation reducts noises and make output more recognizable.(b)Factors for selection of IOA network topologies. r is the Pearson Correlation Coefficient and the output range is HIGHLEVEL minus LOWLEVEL.
Calculating Process
In this part, we will demostrate our calculating process in three sections--Network enumeration, Equations set up and network topologies’ analysis.
== Learn more ==
Analyses and Results
Here we analyzed the results we obtained and found the final right topology.
== Learn more ==
Advanced Model
When the range of input is very large, the IOA networks no longer meet out needs and so we tried to find one semilog-linear topology in this section.
== Learn more ==
References
1 Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K. & Walter, P. (2008). Molecular Biology of the Cell (Garland, New York).
2 Nicolas E. Buchler, Ulrich Gerland, Terence Hwa (2005). Nonlinear protein degradation and the function of genetic circuits, PNAS 102, 9559-9564.
3 John D. Helmann, Barry T. Ballard, Christopher T. Walsh (1998). The MerR Metalloregulatory Protein Binds Mercuric Ion as a Tricoordinate, Metal-Bridged Dimer. Science 247, 946-948.
4 Diana. M, Ralston and Thomas V. O Halloran (1990). Ultrasensitivity and heavy-metal selectivity of the allosterically modulated MerR transcription complex. PNAS 87, 3846-3850.
5 Uri Alon (2007). An Introduction to Systems Biology—Design Principles of Biological Circuits[M], Chapman&Hall/CRC.
6 Wickner, S., Maurizi, M. R. & Gottesman, S.(1999). Posttranslational Quality Control: Folding, Refolding, and Degrading Proteins. Science 286, 1888–1893.
7 W. Ma, A. Trusina, H. El-Samad, W.A. Lim, C. Tang (2009). Defining network topologies that can achieve biochemical adaptation. Cell 138, 760–773.
Download the model part materials
![]() PART ONE
PART ONE
![]() PART TWO
PART TWO
Any problem, please contact with Zhenzhen Yin evamail.pku AT gmail.com Or Yuheng Lu lgdeer AT gmail.com
For more clear pictures, please click on it.
 "
"