Team:ETHZ Basel/Modeling/Chemotaxis
From 2010.igem.org
| Line 51: | Line 51: | ||
|} | |} | ||
| - | == Model based on Mello & Tu (2003) [[Team:ETHZ Basel/Modeling/Chemotaxis#References|[2]]] | + | == Model based on Mello & Tu (2003) == |
| - | + | The model based on Mello & Tu [[Team:ETHZ Basel/Modeling/Chemotaxis#References|[2]]] differs from the one based on Spiro et al. (1997) in a way that it is able to reach perfect and near-perfect adaptation. Mello & Tu investigated robustness of the chemotaxis receptor network, covering the effect of attractant binding through the phosphorylation of CheY. Governing ODEs are derived by applying the law of mass action to the known reactions. Five states of methylation and demethylation of the attractant-bound and free receptors are considered. | |
The published model assumes the binding and unbinding of the ligand to the receptors to be a fast reaction and thus is approximated by a quasi-steady state assumption. Aspartate ligand binding is therefore described by a fraction of total saturation of the chemotaxis receptors. To make it compatible to absolute ligand concentration (as used by the other model), the binding and unbinding reaction rate constants used by Spiro et al. (1997) were used. | The published model assumes the binding and unbinding of the ligand to the receptors to be a fast reaction and thus is approximated by a quasi-steady state assumption. Aspartate ligand binding is therefore described by a fraction of total saturation of the chemotaxis receptors. To make it compatible to absolute ligand concentration (as used by the other model), the binding and unbinding reaction rate constants used by Spiro et al. (1997) were used. | ||
Revision as of 17:43, 27 October 2010
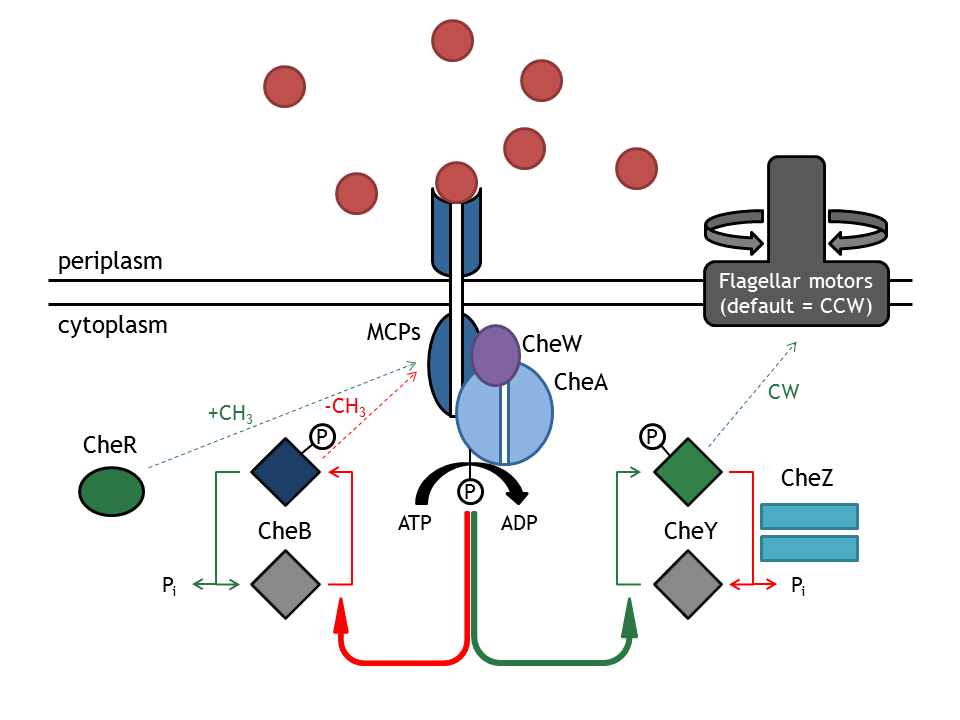
Modeling of the chemotaxis pathway
Background
The complex chemotaxis pathway in E. coli has been well analyzed in the modeling literature and, as the following published models [1], [2], [3], [4] show, many and different assumptions are necessary in order to answer the investigated questions. In the case of E. lemming, the question regarding the chemotaxis pathway is:
How does the output species (CheYp bias) react to perturbations of upstream species?
The chemotaxis network represents the main decision factor in bacterial movement and therefore, it received special attention for the optimal experimental design. In order to achieve a more general consensus prediction of the chemotaxis behavior in E. lemming, it was decided to adapt and extend four different models based on published approaches on modeling the chemotaxis pathway [1], [2], [3], [4].
The interface to the light switch model was defined to be the selected Che species, which is linked to one light-sensitive protein (LSP1). Concentration of this species (LSP1-Che) is determined by the light switch model. Evaluation of the model based on this approach was conducted by changing the concentration of the selected Che species according to a series of time steps reflecting light pulses. This assumes total removal of the species: A red light pulse will activate and dimerize the LSPs and thus result in spatial localization at the anchor and therefore inactivation of the coupled Che protein. In addition to the selected Che species (CheR, B, Y, Z), possible phosphorylated subspecies were analyzed.
Important for analyzing the chemotaxis network in E. lemming is the concentration of the output species CheYp. Threshold of the difference between the two states after activation by light pulses of CheYp concentration is determined, according to predictions of the movement model, regarding an optimization of corresponding tumbling / directed movement frequency. For CheR and Y, the CheYp concentration after light pulse induction decreases in relation to the initial value, while for CheB and Z it increases. Manipulation of CheR and Y concentration therefore have an inverse effect on tumbling / directed movement ratio than CheB and Z. The response of the chemotaxis models was measured by taking the relative amplitude in CheYp concentration between two different light pulses.
Out of the four models of the chemotaxis pathway that our modeling team implemented, only two of them were further investigated in the combined model of E. lemming: Spiro et al. (1997) [1] and Mello & Tu (2003) [2]. These models were chosen not only because they are representative for modeling the chemotaxis pathway, but also because they differ in a few important aspects, as explained later.
| model based on | che species | receptor species |
|---|---|---|
| Spiro et al. | 6 | 12 |
| Mello & Tu | 6 | 15 |
| Barkai & Leibler | 2 | 1 (26 forms) |
| Rao et al. | 4 | 10 |
| original Mello & Tu | 5 | 15 |
Model based on Spiro et al. (1997)
The model based on Spiro et al. (1997) [1] has been used to identify candidates of the chemotaxis receptor pathway by enabling removal or addition of a species upon light induction. For all Che proteins (CheR, Y, B, Z), the concentrations stay below/above the threshold, until they are added again (LSPs are deactivated with far-red light and dimerization is reversed). In terms of aspartate ligand concentration, the best results were obtained for assuming a high ligand concentration (saturation, the methylation level of the receptors is high). For CheY and Z, the reaction times are much faster than for CheB and CheR.

Model based on Mello & Tu (2003)
The model based on Mello & Tu [2] differs from the one based on Spiro et al. (1997) in a way that it is able to reach perfect and near-perfect adaptation. Mello & Tu investigated robustness of the chemotaxis receptor network, covering the effect of attractant binding through the phosphorylation of CheY. Governing ODEs are derived by applying the law of mass action to the known reactions. Five states of methylation and demethylation of the attractant-bound and free receptors are considered.
The published model assumes the binding and unbinding of the ligand to the receptors to be a fast reaction and thus is approximated by a quasi-steady state assumption. Aspartate ligand binding is therefore described by a fraction of total saturation of the chemotaxis receptors. To make it compatible to absolute ligand concentration (as used by the other model), the binding and unbinding reaction rate constants used by Spiro et al. (1997) were used.
Another adaptation was made, since the receptors in the publication of Mello & Tu (2003) were defined by an algebraic equation. To solve the resulting differential algebraic equations, they were included as additional states with a stable equilibrium to fulfill the algebraic equations.
The model based on Mello & Tu (2003) shows similar behavior compared to the adapted Spiro et al. (1997) model.

Model based on Rao et al. (2004) [3]
This chemotaxis model combines the two state model proposed for adaptation by Barkai & Leibler (1997) [4] with the model for the phosphorylation cascade proposed by Sourjik and Berg (2002a).
The receptor methylation is modeled using the method proposed by Barkai & Leibler (1997) with the modifications suggested by Morton-Firth et al. (1999) i.e. CheR binds only to inactive receptors & CheBp binds only to active receptors.
The predictions are quite a similar behavior of the Che proteins, as demonstrated by Spiro et al (1997) [1]. A notable difference is that the response of CheYp level to the change of the level of the other Che proteins is robust to the fluctuations of the ligand (attractant) concentration. In Spiro et al. (1997), the most desirable results were obtained only for higher concentrations of the ligand.
Model based on Barkai & Leibler (1997) [4]

The importance of the two - state chemotaxis network model developed by Barkai & Leibler (1997) lies in the fact that it is the first model to show perfect adaptation over a wide range of parameters (phenomenon also known as robust adaptation). The model is using a single receptor species (MCPs+CheA+CheW) referred to as 'E', which can be in either one of the two states: 'active' or 'inactive'. The active state is characterized by an increased CheA activity, which phosphorylates CheY, therefore inducing tumbling.
The output of the model is the overall activity of the complex, calculated as a weighted average of all the individual forms of the receptor complex and their activity probabilities (i.e. the average number of receptors in the active state). This quantity is functionally dependent on the CheYp level and on the kinetic rates of CheY dynamics, but the actual dependency law is not stated. The activity probabilities are depending on the input value and on the methylation level of the complex.
The receptor complex can exist in either attracted - bound or attracted - free form, it can be successively methylated, up to M methylation sites, and also either in an attractant - bound or attractant - free form. The rates of change of all possibilities resulting from combining the above states render the ODE system proposed by Barkai & Leibler (1997).
The central assumptions of the model are that CheB can only demethylate active receptors, unlike CheR, which methylates both active and inactive ones, and that the methylation and demethylation reactions have slower timescales than the other processes.
As CheYp value was not the direct output of Barkai & Leibler (1997) model and the dependency between the activity of the system and its CheYp level was not clearly stated, we decided to use the models developed Spiro et. al [1] and by Mello & Tu (2003) [2], the latter one also reaching near - perfect adaptation, in developing the complete model of E. lemming.
Download
The chemotaxis models based on Spiro et al. (1997) and Mello & Tu (2003) are included within the Matlab Toolbox and can be downloaded there.
The chemotaxis models based on Barkai & Leibler (1997) and Rao et al. (2004) are provided as independent implementations and can be downloaded from [http://sourceforge.net/projects/ethzigem10/files/additionalChemotaxis.zip/download here].
References
[1] [http://www.pnas.org/content/94/14/7263.full Spiro et al: A model of excitation and adaptation in bacterial chemotaxis. PNAS 1997 94;14;7263-7268.]
[2] [http://www.cell.com/biophysj/retrieve/pii/S0006349503700216 Mello & Tu: Perfect and Near-Perfect Adaptation in a Model of Bacterial Chemotaxis. Biophysical Journal 2003 84;5;2943-2956.]
[3] [http://www.plosbiology.org/article/info:doi/10.1371/journal.pbio.0020049 Rao et al: Design and Diversity in Bacterial Chemotaxis. PLoS Biol 2004;2;2;239-252.]
[4] [http://www.nature.com/nature/journal/v387/n6636/abs/387913a0.html Barkai & Leibler: Robustness in simple biochemical networks. Nature 1997;387;913-917.]
 "
"