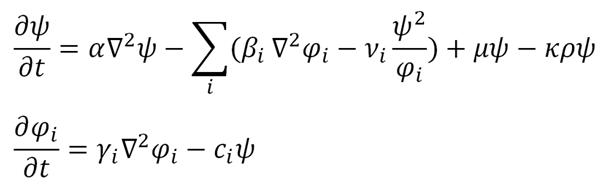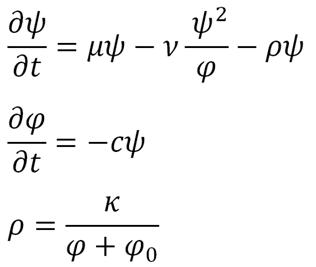Team:HKU-Hong Kong/Modeling
From 2010.igem.org
(→Drastic effects resulted from killing efficiency and initial nutrition density) |
(→Model of bacteria growth and death with killing gene endowed) |
||
| Line 1: | Line 1: | ||
{{:Team:HKU-Hong_Kong/header}} | {{:Team:HKU-Hong_Kong/header}} | ||
=Model of bacteria growth and death with killing gene endowed= | =Model of bacteria growth and death with killing gene endowed= | ||
| - | Generally in the open environment, the population density of | + | |
| + | Generally in the open environment, the population density of bacteria Ψ, the nutrition density φi, and the killing signal density ρ may be modeled by the following system of partial differential equation: | ||
[[Image:Modee1.JPG|400px]] | [[Image:Modee1.JPG|400px]] | ||
| Line 8: | Line 9: | ||
[[Image:Modee2.JPG|180px]] | [[Image:Modee2.JPG|180px]] | ||
| - | Where the functional dependence of ρ is to be determined case by case | + | Where the α,β_i 〖,γ〗_i,μ,ν,κand c_i are parameters to be determined experimentally, and the functional dependence of ρ is to be determined case by case |
| - | ==Special | + | |
| - | In our project, | + | ==Special Case== |
| + | In our project, the lactose analogue, we culture the bacteria in close environment and if the culture is assumed to be homogeneous then the model is simplified to be: | ||
[[Image:Modee3.JPG|230px]] | [[Image:Modee3.JPG|230px]] | ||
Revision as of 13:53, 26 October 2010

Model of bacteria growth and death with killing gene endowed
Generally in the open environment, the population density of bacteria Ψ, the nutrition density φi, and the killing signal density ρ may be modeled by the following system of partial differential equation:
Where the α,β_i 〖,γ〗_i,μ,ν,κand c_i are parameters to be determined experimentally, and the functional dependence of ρ is to be determined case by case
Special Case
In our project, the lactose analogue, we culture the bacteria in close environment and if the culture is assumed to be homogeneous then the model is simplified to be:
This is a system of two asymptotic equations with environment dependent parameters, which will have to be determined experimentally.
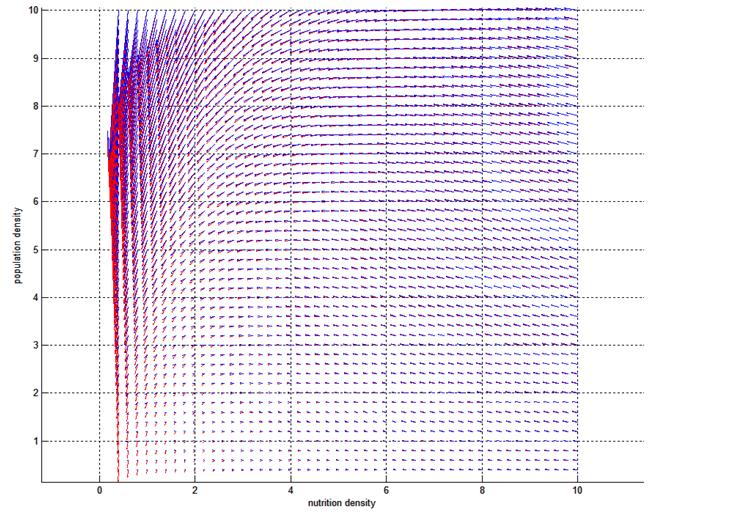
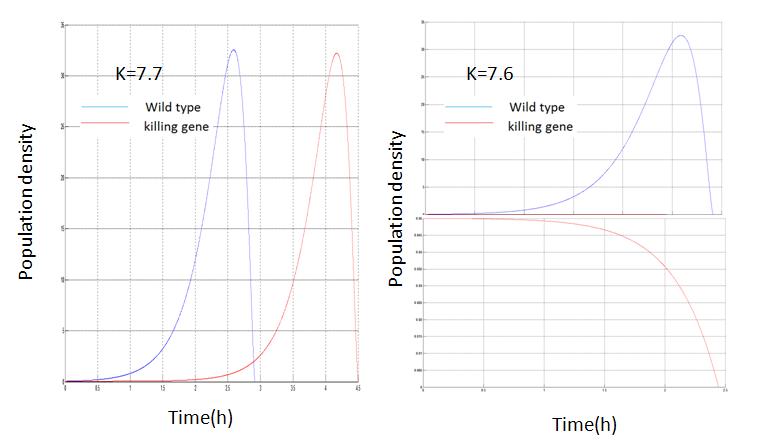
Phase diagram with(blue) and without(red) killing mechanism
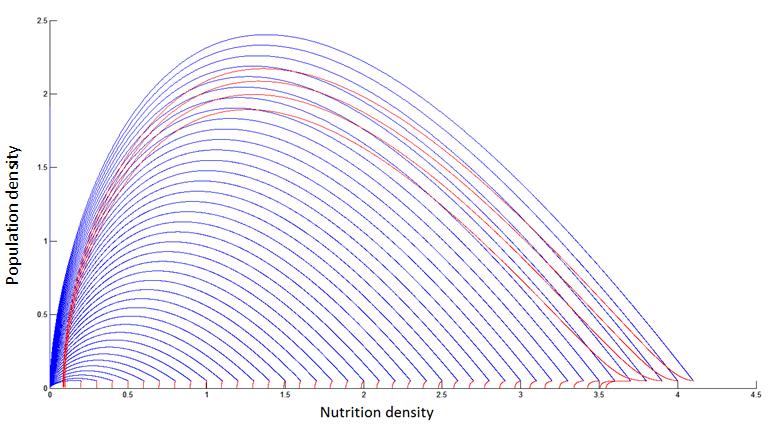
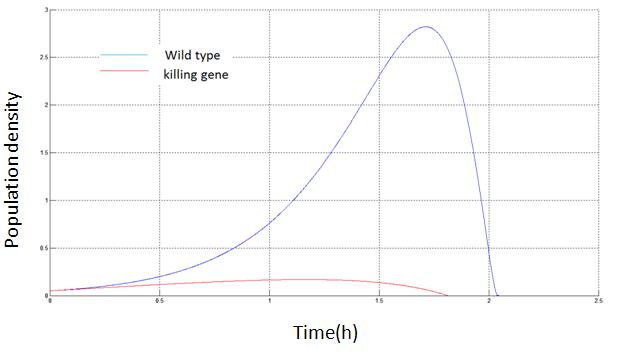
Phase line with(red) and without(blue) killing mechanism
Drastic effects resulted from killing efficiency and initial nutrition density
There is a critical value for killing gene efficiency at a given environment. Below the critical value, the bacteria culture will thrive by suppressing its own survival. Killing a portion of bacteria, the rest will enjoy higher nutrient density for longer time. Above the critical value, the bacteria will kill itself fast enough and hence deprive itself of the chance to take advantage of the death of others.
Remarks
The killing signal should be designed to be independent of the nutrition density.So, if the task of the genetically bacteria has to do with nutrient, as in our lactose analogue, using the nutrient itself as the killing signal is impractical. The idea of a bio-safety net should be further explored with better design of killing signal tailored to the function of the bacterial machinery, for example, time dependent signal.
 "
"